Subsections
Měření elektrických veličin nabývá v současné době na významu. Automatizace
měřícího procesu totiž vyžaduje, aby se i neelektrické veličiny převedly
pomocí čidel na elektrické. Většinou se převádí měřená veličina na
stejnosměrné napětí. Setkávám se však i z převodem neelektrických veličin
na proud, na odpor nebo na "frekvenci" (například na napětí obdélníkového
průběhu, jehož frekvenci je možné měřit počítáním pulzů za zvolený časový
interval pomocí čítače).
Dále se budeme podrobněji zabývat měřením stejnosměrného napětí. Rozlišujeme
dva základní typ voltmetrů:
- Analogové měřicí přístroje ukazují výsledek měření pomocí ručky
(ručkové měřicí přístroje)
- Číslicové (digitální) přístroje dávají výsledné napětí v číslicové
podobě. Rozlišujeme dva základní typy číslicových měřicích přístrojů
- zobrazení jen na displeji, bez možnosti připojení k počítači
- s možností připojení na počítač
K základním elektrickým měření patří současné měření proudu procházejícího
určitým elektronickým prvkem a tomuto proudu odpovídajícího napětí na tomto
prvku. S tímto měřením se setkáváme například při měření voltampérových
charakteristik. K měřenému prvku je nutno současně připojit voltmetr
i ampérmetr, což může způsobit určité problémy, protože tyto přístroje se
pak mohou nepříznivě ovlivňovat.
V zasadě jsou možné dva způsoby připojení. Pro každou konkrétní situaci
je nutné zvolit nejvhodnější metodu, aby chyba měření byla co nejmenší.
=1.00mm
![\begin{picture}(149.02,59.93)\begingroup
\par\dimen0 = 60.00pt
\advance \dime...
...x(0,0)[cc]{$U_v$}}
\put(5.00,59.93){\makebox(0,0)[lt]{METODA A:}}
\end{picture}](img499.png)
V tomto případě proud tekoucí voltmetrem způsobuje, že ampérmetr neměří
proud tekoucí odporem, ale proud větší o proud tekoucí voltmetrem.
Názorně to ukazuje následujíc obrázek, který ukazuje schéma na obrázku
pro případ měření odporu 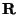 .
.
Označíme-li napětí na odporu 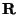 jako
jako 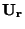 a proud tekoucí odporem jako
a proud tekoucí odporem jako 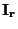 , pak
, pak
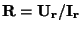 .
.
Napětí na svorkách voltmetru označme 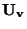 , proud tekoucí ampérmetrem
označme
, proud tekoucí ampérmetrem
označme 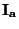 .
.
Je-li vnitřní odpor voltmetru 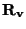 , pak proud
tekoucí voltmetrem
, pak proud
tekoucí voltmetrem
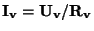 .
.
K určení odpor 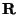 je nutno změřit
je nutno změřit 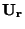 a
a 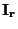 ,
protože
,
protože
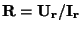 .
.
Měříme
však 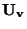 a
a 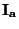 .
.
Platí  , ale
, ale 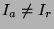
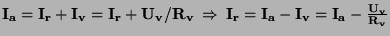
Ampérmetr měří větší proud o proud tekoucí voltmetrem, voltmetr měří
přímo napětí 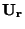 .
.
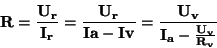 |
(96) |
Tato metoda je vhodná pro případy, kdy svorkový odpor voltmetru 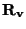 je větší jak měřený odpor R. Zcela nevhodna je pro případy, kdy odpor
je větší jak měřený odpor R. Zcela nevhodna je pro případy, kdy odpor
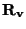 je několikrát menší, než měřený odpor
je několikrát menší, než měřený odpor 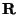 . Pak i po opravách
na vliv voltmetru je chyba měření odporu velká. Používá se například při
měření V/A charakteristiky usměrňovací diody v propustném směru, ale je
zcela nevhodná pro případ měření V/A charakteristiky této diody v závěrném
směru.
Velikost vlivu voltmetru při vlastním měření můžeme snadno posoudit tak,
na chvíli odpojíme jeden přívod voltmetru. Proud ampérmetrem poklesne
o proud tekoucí voltmetrem.
. Pak i po opravách
na vliv voltmetru je chyba měření odporu velká. Používá se například při
měření V/A charakteristiky usměrňovací diody v propustném směru, ale je
zcela nevhodná pro případ měření V/A charakteristiky této diody v závěrném
směru.
Velikost vlivu voltmetru při vlastním měření můžeme snadno posoudit tak,
na chvíli odpojíme jeden přívod voltmetru. Proud ampérmetrem poklesne
o proud tekoucí voltmetrem.
Schéma zapojení pro případ měření velikosti odporu R ukazuje
obrázek. V tomto případě ampérmetr měří přímo proud procházející odporem
R, ale voltmetr měří součet napětí na odporu R a voltmetru.
Opět označme napětí na odporu 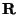 jako
jako 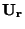 a proud tekoucí odporem jako
a proud tekoucí odporem jako 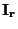 , pak
, pak
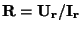 .
.
Napětí na svorkách voltmetru označme 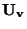 , proud tekoucí ampérmetrem
označme
, proud tekoucí ampérmetrem
označme 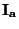 .
.
Je-li vnitřní odpor ampérmetru 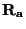 , pak úbytek
napětí na ampérmetru je
, pak úbytek
napětí na ampérmetru je
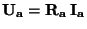 .
.
Platí 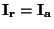 , ale
, ale
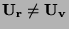 , protože
, protože
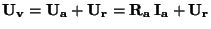
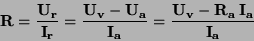 |
(97) |
Poznámka: V případě že měření provádíme v obvodu střídavého proudu,
je nutné navíc počítat s fázovými posuvy ![$[2]$](img260.png) . Pro ideální kondenzátor
při měření pro napětí o frekvenci 50 Hz je fázový 90 stupňů, jak to názorně
ukazuje obrázek.
=1mm
. Pro ideální kondenzátor
při měření pro napětí o frekvenci 50 Hz je fázový 90 stupňů, jak to názorně
ukazuje obrázek.
=1mm
![\begin{picture}(65.00,56.00)
\put(10.00,51.00){\vector(0,-1){31.00}}
\put(10.0...
...ebox(0,0)[lt]{$U_c$}}
\put(65.00,26.00){\makebox(0,0)[lt]{$U_v$}}
\end{picture}](img517.png)
Příklad: Určete chyby při měření odporu oběma metodami (zanedbejte chyby
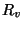 a
a 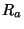 ).
).
Metoda A (viz rovnice (96)):
Metoda B (viz rovnice (97)):
Obrázek:
Závislost relativní chyby odporu vyjádřené v procentech na
napětí použitém při měření. Křížky pro metodu A, kroužky pro metodu B.
|
|
Situaci graficky znázorníme pro následující případ:
Měříme odporu R = 60000  . Použijeme voltmetr o rozsahu
24 V, vnitřním odporu
. Použijeme voltmetr o rozsahu
24 V, vnitřním odporu 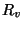 = 120000
= 120000  a třídě přesnosti 1
a ampérmetr o rozsahu 0,6
a třídě přesnosti 1
a ampérmetr o rozsahu 0,6 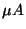 , vnitřním odporu
, vnitřním odporu 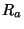 = 1500
= 1500  a třídě
přesnosti 1,5. Z obrázku je zřejmé, že metoda B je o něco přesnější.
Nejdůležitější je však použít vhodné měřící přístroje a správně zvolit rozsahy,
aby bylo možné jak
proud, tak napětí měřit v druhé polovině stupnice.
a třídě
přesnosti 1,5. Z obrázku je zřejmé, že metoda B je o něco přesnější.
Nejdůležitější je však použít vhodné měřící přístroje a správně zvolit rozsahy,
aby bylo možné jak
proud, tak napětí měřit v druhé polovině stupnice.
Poměrně snadno se zvětšují rozsahy ampérmetrů a voltmetrů. U ampérmetru
můžeme zvětšit rozsah pomocí bočníku, u voltmetru pomocí předřadného rezistoru
zapojeného do série s voltmetrem. Je však také možné "zmenšit" rozsah
přístroje tak, že použijeme měřící zesilovač (vytvořený většinou z operačních
zesilovačů). Měřicí zesilovače se používají jak u analogových, tak číslicových
měřicích přístrojů. Měřicí zesilovače však mohou plnit i celou řadu jiných
funkcí například změnu polarity měřeného napětí, převod proudu na napětí,
zvětšují vstupní odpor přístroje atd.
=1.00mm
![\begin{picture}(80.00,73.00)\begingroup
\par\dimen0 = 10.00pt
\advance \dimen...
...makebox(0,0)[lb]{$\frac{1}{R_n} = \frac{1}{R_a} + \frac{1}{R_b}$}}
\end{picture}](img527.png)
Z rovnic uvedených na obrázku vyplývá pro velikost bočníku následující vztah
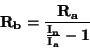 |
(98) |
=1.00mm
![\begin{picture}(80.00,69.08)
\put(40.00,10.00){\circle{10.00}}
\put(20.00,60.0...
...v \: I$}}
\put(80.00,10.00){\makebox(0,0)[lb]{$R_n = R_v + R_p$}}
\end{picture}](img529.png)
Z rovnic uvedených v obrázku vyplývá, že velikost předřadného odporu určíme ze
vztahu.
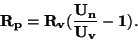 |
(99) |
Poznámka Musíme si uvědomit, že na základním rozsahu je rozlišování mezi
voltmetrem a ampérmetrem u ručkových přístroje jen formální.
Například mikroampérmetr MP 180 z rozsahem
100 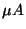 má svorkový odpor 2000
má svorkový odpor 2000  a teče-li jím proud 100
a teče-li jím proud 100 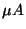 ,
je na jeho svorkách úbytek napětí 200 mV. Můžeme jej proto pokládat i za
voltmetr s rozsahem 200 mV.
,
je na jeho svorkách úbytek napětí 200 mV. Můžeme jej proto pokládat i za
voltmetr s rozsahem 200 mV.
Úkol: Z mikroampérmetru s rozsahem 100 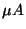 se svorkovým odporem
2000
se svorkovým odporem
2000  vytvořte voltmetr s rozsahem 10 V.
vytvořte voltmetr s rozsahem 10 V.
Řešení: Do série s mikroampérmetrem je nutno zapojit odpor o velikosti
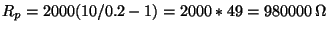 .
.
Jednotlivé typy přístrojů poznáme podle podle následujících značek:
| Magnetoelektrické měřící přístroje (přístroje s otočnou cívkou) |
=0.20mm

|
| Elektromagnetické přístroje (přístroje s pevnou cívkou) |
=0.20mm

|
| Elektrodynamické přístroje |
=0.20mm
|
Magnetoelektrické měřící přístroje (přístroje s otočnou cívkou)
Měření u ručkových přístrojů se provádí na principu vzájemného
silového působení pevné a pohyblivé části. U magnetoelektrického měřícího
přístroje je realizováno silovým působením permanentního magnetu na
vodiče cívky, kterou prochází elektrický proud. Cívka je otočně umístěna
ve vzduchové mezeře pólovitého nástavce silného permanentního magnetu.
V nulové poloze poloze drží cívku dvojice spirálovitých pružin, které
současně slouží k přívodu proudu do cívky.
Měří jen stejnosměrná napětí a proudy. Pro měření střídavých napětí
a proudů je nutno použít převodníku střídavé veličiny na stejnosměrnou.
To můžeme provést jednocestným nebo dvoucestným usměrněním proudu
polovodičovou diodou a nebo pomocí aktivního převodníku s operačními
zesilovači.
Elektromagnetické přístroje (přístroje s pevnou cívkou)
Měřící ústrojí se sestává z cívky, kterou protéká měřený proud
a z feromagnetických plíšků plíšků tvořících otočnou část. U starší provedení
tohoto přístroje se do cívky vtahovalo feromagnetické jádro.
U novějšího provedení tohoto typu přístroje se odpuzují dva shodně
zmagnetované plíšky tj. pevný a otočný (spojený s ručkou přístroje).
Výchylka přístroje je úměrná druhé mocnině efektivní hodnoty proudu tekoucího
cívkou.
Elektrodynamické přístroje (watmetry)
Pracují na principu vzájemného silového působení magnetického pole pevné
a magnetického pole otočné cívky umístěné v dutině první cívky. Protože výchylka
je úměrná součinu dvou veličin, používají se nejčastěji k měření výkonu a jak
stejnosměrného proudu, tak proudu střídavého. Pevnou cívkou prochází proud
do spotřebiče, pohyblivou proud úměrný napětí na spotřebiči
=1mm
![\begin{picture}(120.00,30.08)
\put(0.00,0.00){\framebox (120.00,30.00)[cc]{}}
...
...line(5,4){10.47}}
\put(99.86,3.80){\makebox(0,0)[lb]{$60^\circ$}}
\end{picture}](img535.png)
| Stejnosměrný |
 |
| Střídavý |
 |
| Stejnosměrný i střídavý |
 |
Izolační napětí udává zkušební bezpečnostní napětí. Udává se pomocí
čísla v pěticípé hvězdičce. Je-li například v hvězdičce číslo 2, je
bezpečnostní napětí 2 kV.
Třída přesnosti je uvedena číslem nad značkou druhu měřeného proudu
nebo napětí. Umožňuje určit chybu při měření. Má-li například přístroj
třídu přesnosti 1, tak výrobce zaručuje, ze změřená hodnota se neliší od
skutečné hodnoty o více, jak 1 procento ze zvoleného rozsahu.
Při vlastním měření s voltmetrem i ampérmetrem prochází vždy přístrojem
proud 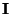 a na svorkách přístroje je úbytek napětí
a na svorkách přístroje je úbytek napětí  .
Vnitřní odpor
.
Vnitřní odpor 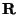 přístroje určíme z Ohmova zákona:
přístroje určíme z Ohmova zákona: 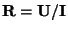 .
Na základě Ohmova zákona můžeme také vnitřní odpor měřicího přístroje
změřit. U většiny přístrojů bývá vnitřní odpor uveden v manuálu nebo i přímo
na měřicím přístroji.
.
Na základě Ohmova zákona můžeme také vnitřní odpor měřicího přístroje
změřit. U většiny přístrojů bývá vnitřní odpor uveden v manuálu nebo i přímo
na měřicím přístroji.
- U voltmetrů bývá uváděn pomocný údaj v
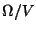 , ze kterého vnitřní odpor
vypočítáme tak, že tento údaj vynásobíme zvoleným rozsahem.
, ze kterého vnitřní odpor
vypočítáme tak, že tento údaj vynásobíme zvoleným rozsahem.
Je-li například na voltmetru uvedeno 5 000 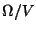 a je zvolen rozsah 24 V, tak
vnitřní odpor voltmetru je 5000 . 24 = 120 000
a je zvolen rozsah 24 V, tak
vnitřní odpor voltmetru je 5000 . 24 = 120 000  .
.
- U ampérmetrů se většinou uvádí úbytek napětí
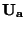 na svorkách
přístroje,
prochází-li přístrojem proud
na svorkách
přístroje,
prochází-li přístrojem proud 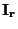 rovný zvolenému rozsahu. Svorkový
odpor ampérmetru
rovný zvolenému rozsahu. Svorkový
odpor ampérmetru
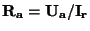 . Například u Avometu je
. Například u Avometu je
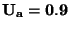 V. Na rozsahu 60 mA je pak vnitřní odpor
0,9/0,06= 15
V. Na rozsahu 60 mA je pak vnitřní odpor
0,9/0,06= 15  .
.
Snahou výrobce je vždy zkonstruovat voltmetr tak, aby jeho svorkový odpor byl
co možná největší a ampérmetr tak, aby jeho svorkový odpor byl co nejmenší.
Je nutné si uvědomit, že vnitřní odpor ampérmetru a voltmetru závisí
jen na zvoleném rozsahu. Na celém měřicím rozsahu je konstantní.
Základní částí číslicových přístrojů je analogově číslicový
(analogově/digitální zkráceně A/D) převodník. Číslicové voltmetry je
možné rozdělit na přístroje komunikující s počítačem a na přístroje,
které mají výstup pouze na zobrazovač.
Číslicové voltmetry, které umožňuje přímou komunikaci s počítačem
se vyrábí ve dvou základních provedeních
- A/D převodník je na měřící kartě, která komunikuje s počítač pomocí
paralelních portů počítače. Měřicí karta bývá často zasunuta přímo
v počítači PC. Takovéto A/D převodníky jsou určeny pro rychlá měření.
Běžně se dosahuje doba převodu kolem 12
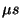 a přenos dat mezi převodníkem
a pamětí počítačem se děje pomocí DMA (přímý přístup do paměti bez účasti
mikroprocesoru počítače). Nejběžnější jsou 12 bitové A/D převodníky.
Výsledkem převodu jsou v tomto případě celá čísla v rozmezí 0 až 4095.
Před A/D převodníkem většinou bývá multiplexer, který umožňuje přepínat na
vstup A/D převodníku napětí z několika kanálů. Používají se jak multiplexery
unipolární, tak bipolární (diferenční).
a přenos dat mezi převodníkem
a pamětí počítačem se děje pomocí DMA (přímý přístup do paměti bez účasti
mikroprocesoru počítače). Nejběžnější jsou 12 bitové A/D převodníky.
Výsledkem převodu jsou v tomto případě celá čísla v rozmezí 0 až 4095.
Před A/D převodníkem většinou bývá multiplexer, který umožňuje přepínat na
vstup A/D převodníku napětí z několika kanálů. Používají se jak multiplexery
unipolární, tak bipolární (diferenční).
- A/D převodník je mimo vlastní počítač a komunikuje s počítačem
pomocí standardního rozhraní RS 232C nebo HPIB. V tomto případě se komunikace
mezi měřicím přístrojem a počítačem děje tak, že se informace přenáší
ve formě řetězců (přenáší se ASCII kódy písmen a číslic).
Pro měřený rychlých časových průběhů napětí slouží digitální osciloskopy.
V tomto případě se výsledky analogově číslicového převodu ukládají do
pamětí osciloskopu a z této paměti se po měření zobrazí na obrazovce nebo
přenesou do počítače.
Některé typy přístrojů (například i u nás vyráběný voltmetr M1T 330
a multimetr M1T 380 z Metry Blansko) jsou sami řízeny mikroprocesory
zabudovanými v přístrojích, které zajišťují automatickou kalibraci
a testování správné funkce přístroje. Mají zabudovaný napěťový normál
a přístroj dokáže sám korigovat vliv teplotních změn a změny parametrů
součástek v děličích vlivem stárnutí.
Poznámka: Z hlediska teorie chyb je jasné, ze A/D převodníky určené
pro rychlá měření měří napětí s menší přesnosti, než A/D převodníky určené
pro pomalá měření.
Například u voltmetru M1T 330 se napětí měří tak, že po příchodu příkazu
k měření voltmetr počká, až síťové napětí prochází 0 a doba A/D převodu
je rovna 1 periodě síťového napětí. Tím se vyloučí rušení měření síťovým
napětím.
V praxi se používá celá řada analogově číslicových převodů. Podle ![$[10]$](img547.png) nejběžnější jsou následující způsoby převodu:
nejběžnější jsou následující způsoby převodu:
- komparační metody
- kompenzační metody
- integrační metody
Komparační metody převodu vychází z porovnávání měřeného napětí
s kvantovaným referenčním napětí. Porovnávání se může uskutečnit se všemi
možnými úrovněmi převodu najednou a nebo postupně. Podle toho rozlišujeme
paralelní a postupné komparační převodníky. Nejtypičtějším příkladem
je paralelní komparační převodník, protože je velice rychlý. Doba převodu
je dána jen zpožděním komparátoru a proto se doba převodu může pohybovat
kolem 10 ns. Nevýhodou je složitost převodníku, který musí obsahovat tolik
komparátorů, kolik je převáděných úrovní. Proto se takovýto převodník
používá maximálně pro 8-bitové převodníky.
Kompenzační metody jsou založeny na kompenzaci měřeného napětí
napětím vytvořeným vhodným způsobem. Podle způsobu jakým se mění
kompenzační napětí dělíme převodníky na převodníky s konstantním přírůstkem
a na převodníky s odstupňovaným přírůstkem. Nejznámější je metoda postupné
aproximace, je to metoda s odstupňovaným přírůstkem. Přírůstky kompenzačního
napětí jsou odstupňovány podle vah bitů číslicového slova.
Doba převodu bývá řádově 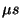 .
Blokové schéma převodníku s postupnou aproximací ukazuje obrázek. Obvod se
skládá z číslicově analogového převodníku, komparátoru, aproximačního
registru a generátoru hodinového kmitočtu o frekvenci
.
Blokové schéma převodníku s postupnou aproximací ukazuje obrázek. Obvod se
skládá z číslicově analogového převodníku, komparátoru, aproximačního
registru a generátoru hodinového kmitočtu o frekvenci 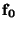 .
Převodník postupně srovnává měřené napětí s napětími odpovídajícími
vahám jednotlivým bitů. Začne se od nejvyššího bitu (Moust significant
bit MSB) a postupně se přidávají jednotlivá váhová napětí a podle
reakce komparátoru se na danou pozici dosadí buď logická 1 nebo logická 0.
Výsledek měření tedy vždy dostaneme u n-bitového převodníku po n taktech.
Na výstupu TP převodník signalizuje počítači konec převodu a počítač přečte
data D1 až Dn.
.
Převodník postupně srovnává měřené napětí s napětími odpovídajícími
vahám jednotlivým bitů. Začne se od nejvyššího bitu (Moust significant
bit MSB) a postupně se přidávají jednotlivá váhová napětí a podle
reakce komparátoru se na danou pozici dosadí buď logická 1 nebo logická 0.
Výsledek měření tedy vždy dostaneme u n-bitového převodníku po n taktech.
Na výstupu TP převodník signalizuje počítači konec převodu a počítač přečte
data D1 až Dn.
=aprox.pic
Obr.: Převodník s postupnou aproximací
=integrac.pic
Obr.: Integrační převodník
Integrační metody jsou založeny na integraci měřeného napětí
a mezipřevodu na časový interval nebo frekvenci. Důležitou vlastností této
metody je filtrace rušivých signálů vyšších frekvencí. Doba integrace
se totiž volí jako násobek periody rušivého signálu. Nevýhodou je dlouhý
čas převodu (desítky a stovky ms).
Integrační metoda má celou řadu modifikaci. Nejpoužívanější je
však převodník s dvojitou (dvoutaktní) integraci, dvojnásobným pilovitým
průběhem) ![$[10]$](img547.png) .
Blokové schéma převodníku ukazuje obrázek. Po zadanou dobu
.
Blokové schéma převodníku ukazuje obrázek. Po zadanou dobu 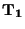 (první takt) se integruje měřené napětí
(první takt) se integruje měřené napětí  . Hodnotě naintegrované
v druhém taktu je pak úměrný číselný údaj převodníku. Přesnost převodu je
dána stabilitou zdroje referenčního napětí
. Hodnotě naintegrované
v druhém taktu je pak úměrný číselný údaj převodníku. Přesnost převodu je
dána stabilitou zdroje referenčního napětí 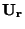 a v podstatě nezávisí
na časové stálosti rezistoru
a v podstatě nezávisí
na časové stálosti rezistoru 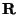 , kapacitoru
, kapacitoru 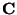 a zesílení
operačního zesilovače
a zesílení
operačního zesilovače 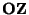 , protože doba jednoho převodu je rovna zlomku
sekundy a po tuto dobu je možné udržet vlastnosti těchto součástek
stálé.
Před začátkem měření je sepnut spínač
, protože doba jednoho převodu je rovna zlomku
sekundy a po tuto dobu je možné udržet vlastnosti těchto součástek
stálé.
Před začátkem měření je sepnut spínač 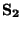 a tím vybit kapacitor
a tím vybit kapacitor 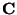 .
V okamžiku začátku měření se rozpojí spínač
.
V okamžiku začátku měření se rozpojí spínač 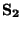 a spínač
a spínač 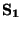 připojí na integrátor měřené napětí
připojí na integrátor měřené napětí  . Výstupní napětí integrátoru
. Výstupní napětí integrátoru
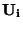 lineárně roste. Současně se sepnutím spínače
lineárně roste. Současně se sepnutím spínače 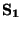 se
se otevře hradlo a čítač počítá impulzy o kmitočtu
se
se otevře hradlo a čítač počítá impulzy o kmitočtu 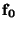 . Jakmile se
čítač naplní, vydá impulz
. Jakmile se
čítač naplní, vydá impulz 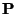 (naplnění trvá dobu
(naplnění trvá dobu 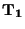 ), obvod
řízení přepne spínač
), obvod
řízení přepne spínač 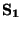 na referenční napětí
na referenční napětí 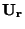 , jehož
polarita je opačná než
, jehož
polarita je opačná než  . Současně s tím se znovu plní čítač a to
po tzv. přetečení na konci intervalu
. Současně s tím se znovu plní čítač a to
po tzv. přetečení na konci intervalu 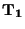 , protože hradlo zůstává
otevřeno. Výstupní napětí integrátoru klesá k nule. V okamžiku, kdy dosáhne
nuly, zareaguje napěťový komparátor
, protože hradlo zůstává
otevřeno. Výstupní napětí integrátoru klesá k nule. V okamžiku, kdy dosáhne
nuly, zareaguje napěťový komparátor 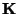 a obvod řízení uzavře hradlo.
Tím končí druhý takt
a obvod řízení uzavře hradlo.
Tím končí druhý takt 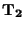 . Nový obsah čítače je přes dekodér přenesen na
zobrazovač a ukazuje změřené napětí. Poté je čítač vynulován signálem
. Nový obsah čítače je přes dekodér přenesen na
zobrazovač a ukazuje změřené napětí. Poté je čítač vynulován signálem
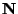 a je vybit kapacitor
a je vybit kapacitor 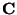 sepnutím spínače
sepnutím spínače 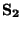 a celý
cyklus se může opakovat.
Počet impulzů v čítači při vybíjení referenčním napětím je
a celý
cyklus se může opakovat.
Počet impulzů v čítači při vybíjení referenčním napětím je
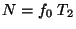 .
Pro vlastní integrátor platí:
.
Pro vlastní integrátor platí:

neboť po nabití kapacitoru v době 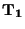 klesne napětí na něm za
dobu
klesne napětí na něm za
dobu 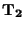 na nulu, takže:
na nulu, takže:
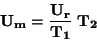 |
(100) |
Počet impulzů v čítači po druhé integraci je přímo úměrný měřenému napětí.
Pracuje-li převodník pro obě polarity napětí musí se měnit i polarita
referenčního napětí.
Rychlost analogově číslicového převodníku s dvojitou integraci můžeme zvýšit,
rozdělíme-li čas, ve kterém integrujeme referenční napětí na dva časové úseky,
přičemž strmost výstupního napětí z integračního obvodu v prvním úseku je
větší než ve druhém úseku. Mluvíme pak o třítaktní integrační metodě se
snižováním náboje již v prvním taktu. Na tomto principu pracuje i převodník
v multimetru M1T 380 z Metry Blansko.
V praxi se setkáme i s jinými způsoby dělení analogově číslicových
převodníků. Například v ![$[11]$](img563.png) se setkáme s následujícím rozdělením.
se setkáme s následujícím rozdělením.
- Převodníky bez zpětné vazby, které bezprostředně
porovnávají vstupní analogové napětí s referenčním napětím.
Výsledkem porovnání je výstupní slovo analogově číslicového převodníku
- Převodníky se zpětnou vazbou, které porovnávají v porovnávacím
obvodu vstupní analogové napětí s analogovým napětím odvozeným z postupně
generovaného výstupního slova. Převod je ukončen v okamžiku rovnosti obou
porovnávaných napětí.
Převodníky je možné rozdělit i na:
- Synchronní - převod probíhá v určitém počtu kroků synchronně
s hodinovými impulzy.
- Asynchronní - převod se též může uskutečnit v několika krocích,
ale doba trvání jednotlivých kroků závisí výhradně na časové odezvě dílčích
obvodů převodníku, resp. na jejich zpoždění.
Jiné rozlišení převodníků je na
- Přímé - převádí vstupní analogové napětí přímo na výstupní slovo
- Nepřímé - převádí nejprve určitým obvodem vstupní analogové napětí
na jinou analogovou veličinu (například na dobu trvání impulzu, kmitočet
sledu impulzů) a dalším obvodem získanou (odvozenou) analogovou veličinu
převádějí na číslicový tvar.
;'';''
Při volbě analogově číslicového převodníku
jsou z hlediska teorie chyb nejdůležitější následující parametry:
- rychlost převodu
- nelinearitu převodu (integrální i diferenciální)
- rozlišovací schopnost (počet bitů ve výstupním slovu)
- chyba způsobenou dobou vzorkování
- teplotní stabilitu
- vstupní impedanci
- šum (resp. jeho vliv na přesnost měření)
Rychlost převodu
Opakovací kmitočet vzorkování musí být dostatečně vysoký
vzhledem k nejvyšší složce měřeného vstupního napětí.
Na druhé straně vysoký opakovací kmitočet klade vysoké nároky na technické
vybavení.
Nejnižší přípustný opakovací kmitočet vzorkování je určen
Shanonovým-Kotelnikovým vzorkovacím teorémem, který říká, že pro nezkreslený
přenos je nezbytné přenést alespoň dva body amplitudy nejvyšší kmitočtové
složky analogového signálu. Kmitočet vzorkování musí tedy být vyšší, jak
dvojnásobek nejvyšší kmitočtové složky spektra analogového signálu
Rozlišovací schopnost
Je určena počtem úrovní, do kterého jsme rozdělili rozsah vstupního
analogového napětí. Jelikož výstupní slovo analogově číslicového převodníku
se obvykle vyjadřuje v přirozeném dvojkovém kódu, je často rozlišovací
schopnost vyjádřena počtem bitů ve výstupní slovu.
| Počet bitů |
Rozsah výstupního slova |
Rozlišovací schopnost |
| n |
0 až 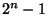 |
 |
| 8 |
0 až 255 |
1/255 |
| 10 |
0 až 1023 |
1/1023 |
| 12 |
0 až 4095 |
1/4095 |
| 16 |
0 až 65535 |
1/65535 |
Kvantizační chyba a nelinearita
Výstupní napětí může nabývat libovolnou diskrétní hodnotu v mezích vstupního
rozsahu. Například u 12bitové převodníku jsou výsledkem měření celá čísla
v rozmezí 0 až 4095. Tímto procesem vzniká chyba, kterou nazýváme
kvantizační chybou. Kvantizační chyba může dosáhnout maximálně hodnoty,
která odpovídá
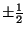 nejnižšího bitu výstupního slova převodníku.
Kvantizační chybu je možné zmenšit použitím více bitů ve výstupním slovu
převodníku.
nejnižšího bitu výstupního slova převodníku.
Kvantizační chybu je možné zmenšit použitím více bitů ve výstupním slovu
převodníku.
Možné chyby převodníku ukazuje následující obrázek, který pro přehlednost
ukazuje tříbitový převodník, jehož výstupní slovo obsahuje 3 bity
| Dekadicky |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Binárně |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
| Výstup |
0 |
1/8 |
2/8 |
3/8 |
4/8 |
5/8 |
6/8 |
7/8 |
=0.75mm
![\begin{picture}(100.10,100.10)
\put(19.79,20.02){\vector(1,0){80.31}}
\put(19....
...
\put(19.67,12.00){\makebox(0,0)[lt]{a) Ideální charakteristika}}
\end{picture}](img567.png)
=posun.pic
=0.75mm
![\begin{picture}(100.10,100.10)
\put(19.79,20.02){\vector(1,0){80.31}}
\put(19....
...
\put(20.67,11.50){\makebox(0,0)[lt]{c) Chyba zisku převodníku }}
\end{picture}](img568.png)
=neli.pic
U převodníku se první přechod z jedné úrovně na druhou nemusí vykonat
přesně na úrovni 1/2 hodnoty odpovídající nejbližšímu bitu ve výstupním
slovu. Vzniká chyba způsobená napěťovým posunem ( obrázek b) ).
Dalšími možnými chybami je změna měřítka (chyba zisku - obrázek c) )
a nelinearita (obrázek c)).
Integrální a diferenciální nelinearita
Na obrázku a) jsme spojili středy kvantizačních úrovní spojnicí a.
Je-li tato spojnice přímkou, je převod lineární.
Integrální nelinearitu 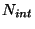 definujeme rozdílem mezi maximální
a minimální strmostí spojnice,
definujeme rozdílem mezi maximální
a minimální strmostí spojnice,
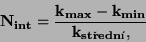 |
(101) |
kde 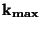 je maximální strmost spojnice a,
je maximální strmost spojnice a, 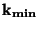 minimální strmost spojnice,
minimální strmost spojnice,
 je střední strmost spojnice,
přičemž strmost
je střední strmost spojnice,
přičemž strmost 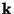 je definována vztahem
je definována vztahem
Typická integrální nelinearita desetibitového analogově číslicového
převodníku s postupnou aproximací je větší než 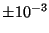 .
U ideálního analogově číslicového převodníku jsou rozdíly mezi jednotlivými
dílčími úrovněmi stejně velké. Velikost těchto rozdílů jsme na obrázku a)
označili symbolem
.
U ideálního analogově číslicového převodníku jsou rozdíly mezi jednotlivými
dílčími úrovněmi stejně velké. Velikost těchto rozdílů jsme na obrázku a)
označili symbolem  . Jsou-li tyto rozdíly různě velké, vyskytuje
se u příslušného převodníku diferenciální nelinearita. Diferenciální
nelinearita
. Jsou-li tyto rozdíly různě velké, vyskytuje
se u příslušného převodníku diferenciální nelinearita. Diferenciální
nelinearita
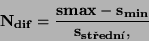 |
(102) |
kde 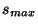 je maximální,
je maximální, 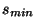 minimální a
minimální a 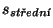 střední
hodnota rozdílů dílčích úrovní.
Například u 10 bitového převodníku s postupnou aproximací bývá diferenciální
nelinearita větší než
střední
hodnota rozdílů dílčích úrovní.
Například u 10 bitového převodníku s postupnou aproximací bývá diferenciální
nelinearita větší než 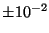 .
.
Chyba způsobená dobou vzorkování
Dobou převodu rozumíme časový interval, za který analogově číslicový
převodník převede analogové napětí do digitální podoby.
Pro rychle měnící se měřené signály je vhodné zařadit před vlastní
převodník vzorkovací obvod s analogovou pamětí. Tento obvod odebere
rychle vzorek analogového napětí během doby 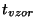 a hodnotu si
zapamatuje alespoň pod dobu
a hodnotu si
zapamatuje alespoň pod dobu 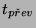 .
.
Například pro převod sinusového napětí
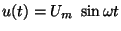 nastane
největší chyba vlivem doby vzorkování zahájíme-li vzorkování při průchodu
sinusového napětí nulou, protože v tomto okamžiku má sinusový průběh
maximální strmost.
nastane
největší chyba vlivem doby vzorkování zahájíme-li vzorkování při průchodu
sinusového napětí nulou, protože v tomto okamžiku má sinusový průběh
maximální strmost.
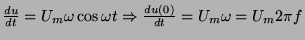 . Aproximujeme-li kolem bodu
. Aproximujeme-li kolem bodu
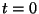 sinusové napětí přímkou
sinusové napětí přímkou
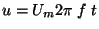 , pak za dobu
převodu
, pak za dobu
převodu 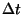 nastane změna sinusového napětí
nastane změna sinusového napětí
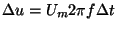 . Pro sinusové napětí jde o maximální možnou
chybu. Z předcházejícího vztahu je možné určit maximální kmitočet sinusového
napětí pro zvolenou přípustnou chybu způsobenou dobou převodu
. Pro sinusové napětí jde o maximální možnou
chybu. Z předcházejícího vztahu je možné určit maximální kmitočet sinusového
napětí pro zvolenou přípustnou chybu způsobenou dobou převodu
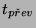 (nebo dobou vzorkování).
(nebo dobou vzorkování).
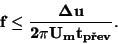 |
(103) |
Obrázek:
Porovnání měření 12bitovým A/D převodníkem karty IP-Coach a METEXu M 3850
|
|
Obrázek:
Obdoba předcházejícího obrázku, jen šum karty IP-Coach je
odstraněn mnohonásobným opakování měření
|
|
Porovní přenosti měření různých A/D převodníků je nutné provádět opatrně,
abychom porovnávali srovnatelné. Nazorně to objasňuje následující obrázek,
který porovnává reprodukovatelnost měření napětí pro
multimetr METEX M 3850 a 12bitového A/D převodníku školního systému IP-Coach.
Bylo provedeno 300 měření a výsledek byl znárorněn graficky.
Začátečník by usoudil, že multimetr METEX M 3850 měří jasně přesněji.
Měřící karta IP-Coach je však schopna provest více jak 10 000 měření za sekundu
naproti tomu METEX provede maximalně 10 měření za sekundu a hodí se jen
pro měření pomalu se měnících napětí. Měříme-li takovéto napětí pomocí
IP-Coach je možné za 0.1s provést až 1000 měření a šum odstranit tak, že
z naměřených hodnot vypočteme aritmetický průměr. Jak je vidět z následujícho
obrázku šum se dá v tomto případě výrazně zmenšit.
Větší problémem jsou systematické chyby měření. Pro měřená napětí jsou
chyby udavaná výrobci obou zařízení kolem 2 mV.
;'';''
=impedanc.pic
Měření mohou ovlivnit stejnosměrná nebo střídavá rušivá napětí superponovaná
na měřený signál. Podle ![$[10]$](img547.png) rozlišujeme rušení souhlasné
rozlišujeme rušení souhlasné 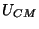 (Common Mode) a sériové
(Common Mode) a sériové 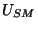 (Series Mode).
Souhlasné rušivé napětí
(Series Mode).
Souhlasné rušivé napětí 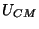 působí ve stejné fázi na vstupních
svorkách H a L číslicového voltmetru a způsobuje rušivý proud
působí ve stejné fázi na vstupních
svorkách H a L číslicového voltmetru a způsobuje rušivý proud  ,
který vytváří na rezistoru nevyvážených přívodů chybové napětí.
Sériové rušivé napětí
,
který vytváří na rezistoru nevyvážených přívodů chybové napětí.
Sériové rušivé napětí 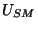 se přičítá přímo k měřenému napětí
se přičítá přímo k měřenému napětí 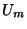 .
Zdrojem stejnosměrného rušivého napětí jsou v provozu nejčastěji
termoelektrická napětí ve vstupním obvodu voltmetru a zbytková napětí přepínače
na vstupu voltmetru.
Zdrojem střídavého rušivého napětí je často napětí indukované do vstupních
obvodů multimetru elektromagnetickým polem síťových vodičů, nebo zvlněním
napětí napájecího zdroje.
Schopnost číslicového voltmetru potlačit souhlasné rušení je
charakterizována činitelem potlačení součtového rušení
.
Zdrojem stejnosměrného rušivého napětí jsou v provozu nejčastěji
termoelektrická napětí ve vstupním obvodu voltmetru a zbytková napětí přepínače
na vstupu voltmetru.
Zdrojem střídavého rušivého napětí je často napětí indukované do vstupních
obvodů multimetru elektromagnetickým polem síťových vodičů, nebo zvlněním
napětí napájecího zdroje.
Schopnost číslicového voltmetru potlačit souhlasné rušení je
charakterizována činitelem potlačení součtového rušení
![\begin{displaymath}\bf
CMRR = 20 \log \frac {U_{CM}}{\Delta U} \; \; \; [dB]
\end{displaymath}](img597.png) |
(104) |
Schopnost číslicového voltmetru potlačit sériové rušení je charakterizována
činitelem potlačení sériového rušení
![\begin{displaymath}\bf
SMRR = 20 \log \frac {U_{NM}}{\Delta U} \; \; \; [dB],
\end{displaymath}](img598.png) |
(105) |
kde 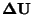 je chyba údaje měřidla způsobená rušením.
Nejčastěji se uvádí CMRR pro
je chyba údaje měřidla způsobená rušením.
Nejčastěji se uvádí CMRR pro
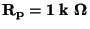 nebo pro
nebo pro
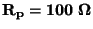 (údaj je větší o 20 dB)
Čím větší bude impedance
(údaj je větší o 20 dB)
Čím větší bude impedance 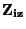 , tím menší bude
, tím menší bude 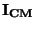 .
Velké izolační impedance
.
Velké izolační impedance 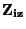 dosáhneme plovoucím vstupem
číslicového voltmetru (obě vstupní svorky L, H jsou izolovaně
odděleny od kostry přístroje).
dosáhneme plovoucím vstupem
číslicového voltmetru (obě vstupní svorky L, H jsou izolovaně
odděleny od kostry přístroje).
Sériové rušení účinně potlačíme u stejnosměrného měřeného napětí, jestliže
rušivý signál má střídavý periodický průběh. K potlačení používáme filtrace
pasivními a aktivními filtry nebo výše popsanou integraci měřeného napětí.
Potlačení sériového rušení pomocí filtrů však zmenšuje rychlost měření.
Voltmetry a multimetry určené k přesnému měření napětí
mívají pro připojení napětí 3 vstupní zdířky označené G, L a H.
Svorky G a L bývají propojeny. Zasuneme-li banánek do svorky G dojde
k rozpojení těchto svorek. Jsou možné dva základní způsoby připojení
měřeného napětí:
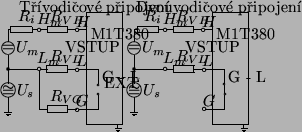
- Třívodičové zapojení má vyšší činitel potlačení
souhlasného ss a st napětí ve srovnání s dvouvodičovým zapojením.
Napětí přivedeme pomocí vodičů L a H, které jsou stíněny vodičem připojeným
do svorky G. Je nutno dbát na to, aby svorky
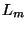 a
a  byly propojeny
vodičem s co nejmenším odporem, aby se potlačilo rušení souhlasným napětím.
byly propojeny
vodičem s co nejmenším odporem, aby se potlačilo rušení souhlasným napětím.
- Dvouvodičové zapojení zapojení využívá jen svorek L a H. Svorka G je
uvnitř přístroje propojena se svorkou G. K přivedení napětí je nejvýhodnější
použít koaxiální kabel, jehož stínění se připojí do svorky L. Činitel
potlačení souhlasných napětí je nižší, než u třívodičového zapojení.
Situaci pro multimetr M1T 380 názorně ukazuje následující obrázek:
=1.00mm
;''
| M1T 330 |
|
|
|
|
M1T 380 |
|
|
|
|
|
|
| Rozsah |
|
Citlivost |
|
Vstupní odpor |
Rozsah |
|
C1 |
|
C2 |
|
Vstupní odpor |
| 300 |
mV |
10 |
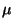 V V |
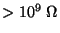 |
150 |
mV |
1 |
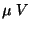 |
100 |
nV |
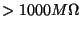 |
| 3 |
V |
100 |
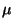 V V |
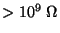 |
1,5 |
V |
10 |
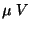 |
1 |
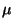 V V |
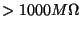 |
| 30 |
V |
1 |
mV |
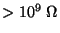 |
15 |
V |
100 |
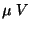 |
10 |
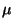 V V |
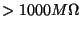 |
| 300 |
V |
10 |
mV |
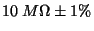 |
150 |
V |
1 |
mV |
100 |
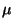 V V |
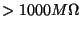 |
C1 je citlivost pro integrační dobu 20 ms a 200 ms.
C2 je citlivost pro integrační dobu 2 s.
MH - měřená hodnota, MHMR - zvolený rozsah
| Základní chyba M1T 330 |
Základní chyba M1T 380 |
| 0,01 % MH + 0,01 % MHMR |
100 ppm MH + 20 ppm MHMR + chyba vnějšího normálu |
| Přídavná teplotní chyba M1T 330 |
Přídavná teplotní chyba M1T 380 |
| (0,002 % MH + 0.002 % MHMR)/K |
(20 ppm MH + 10 ppm MHMR)/K |
Potlačení souhlasného napětí při rozvážení 1 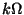 |
M1T 330 |
M1T 380 |
| ss napětí |
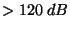 |
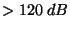 |
| st napětí síťového kmitočtu |
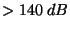 |
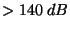 |
| Potlačení sériového rušivého napětí síťového kmitočtu |
M1T 330 |
Doba integrace |
M1T 380 |
| |
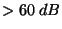 |
200 ms |
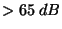 |
| |
|
20 ms |
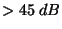 |
| |
|
2 s |
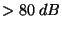 |
U měřící karty PCL -818L uvádí pro analogové vstupy výrobce
následující parametry:
| Anglicky |
|
Česky |
|
| Channels: |
16 singel-endes or 8 differential |
Kanály: |
16 unipolárních nebo 8 bipolárních |
| Resolution: |
12 bits |
Rozlišení: |
12 bitů |
| Conversion type: |
Successive approximation |
Typ převodníku: |
s postupnou aproximaci |
| Conversion rate: |
40 kHz max |
Frekvence vzorkování: |
do 40 kHz |
| Accuracy: |
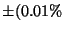 of reading) of reading) 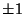 bit bit |
Přesnost: |
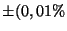 měřené hodnoty) měřené hodnoty) 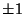 bit bit |
| Linearity: |
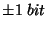 |
Linearita: |
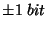 |
| Data transfer: |
Program, |
Přenos dat: |
programově, |
| |
interrupt or DMA |
|
pomocí přerušení nebo DMA |
Poznámka: Karta PCL 818L je výrobkem firmy ADVANTECH, obdobnou kartu
s označením DAS-16 vyrábí i firma KEITHLEY a pod označením AX 5411 ji vyrábí
i firma AXIOM. Tato karta of firmy AXIOM je součástí
školního měřicího systému ISES Profesionál.
Pro měřící kartu AXIOM uvádí výrobce následujíc parametry:
| Anglicky |
|
Česky |
|
| Number of inputs |
16 single-ended |
Počet vstupů |
16 |
| Resolutino |
12 bits |
Rozlišení |
12 bitů |
| Sampling Rate |
60 kHz max. |
Vzorkovací frekvence |
60 KHz max. |
| A/D Conversion Time |
15 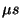 max. max. |
Doba převodu |
15 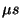 max. max. |
| Channel Acquisition Time |
5 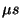 max. max. |
|
5 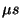 max. max. |
| System Accuracy |
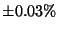 FSR FSR |
|
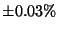 MHMR MHMR |
| Nonlinearity |
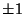 LSB LSB |
Nelinearita |
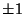 LSB LSB |
| Differential Nonlinerity |
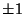 LSB LSB |
Diferenciální nelinearita |
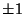 LSB LSB |
| Inherent Quantizing Error |
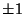 LSB LSB |
Kvantizační chyba |
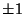 LSB LSB |
| Zero Drift: Bipolar |
17 ppm of FSR/C |
17 ppm MHMR/K |
|
| Gain Drift |
30 ppm of FSR/C |
|
30 ppm MHMR/K |
Anglická zkratka FSR se česky překládá jako MHMR tj. maximální hodnota
měřícího rozsahu
© František Šťastný, 1997
![\begin{picture}(149.02,59.93)\begingroup
\par\dimen0 = 60.00pt
\advance \dime...
...x(0,0)[cc]{$U_v$}}
\put(5.00,59.93){\makebox(0,0)[lt]{METODA A:}}
\end{picture}](img499.png)
![]() .
.
![]() jako
jako ![]() a proud tekoucí odporem jako
a proud tekoucí odporem jako ![]() , pak
, pak
![]() .
.
![]() , proud tekoucí ampérmetrem
označme
, proud tekoucí ampérmetrem
označme ![]() .
.
![]() , pak proud
tekoucí voltmetrem
, pak proud
tekoucí voltmetrem
![]() .
.
![]() je nutno změřit
je nutno změřit ![]() a
a ![]() ,
protože
,
protože
![]() .
.
![]() a
a ![]() .
.
![]() , ale
, ale ![]()
![]()
![]() .
.
![]() jako
jako ![]() a proud tekoucí odporem jako
a proud tekoucí odporem jako ![]() , pak
, pak
![]() .
.
![]() , proud tekoucí ampérmetrem
označme
, proud tekoucí ampérmetrem
označme ![]() .
.
![]() , pak úbytek
napětí na ampérmetru je
, pak úbytek
napětí na ampérmetru je
![]() .
.
![]() , ale
, ale
![]() , protože
, protože
![]()
![\begin{picture}(65.00,56.00)
\put(10.00,51.00){\vector(0,-1){31.00}}
\put(10.0...
...ebox(0,0)[lt]{$U_c$}}
\put(65.00,26.00){\makebox(0,0)[lt]{$U_v$}}
\end{picture}](img517.png)
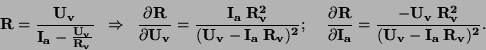
![\includegraphics[height=10cm, width=\textwidth, keepaspectratio=false]{metodaab}](img524.png)
![\begin{picture}(80.00,73.00)\begingroup
\par\dimen0 = 10.00pt
\advance \dimen...
...makebox(0,0)[lb]{$\frac{1}{R_n} = \frac{1}{R_a} + \frac{1}{R_b}$}}
\end{picture}](img527.png)
![\begin{picture}(80.00,69.08)
\put(40.00,10.00){\circle{10.00}}
\put(20.00,60.0...
...v \: I$}}
\put(80.00,10.00){\makebox(0,0)[lb]{$R_n = R_v + R_p$}}
\end{picture}](img529.png)
![\begin{picture}(120.00,30.08)
\put(0.00,0.00){\framebox (120.00,30.00)[cc]{}}
...
...line(5,4){10.47}}
\put(99.86,3.80){\makebox(0,0)[lb]{$60^\circ$}}
\end{picture}](img535.png)
![]() a na svorkách přístroje je úbytek napětí
a na svorkách přístroje je úbytek napětí ![]() .
Vnitřní odpor
.
Vnitřní odpor ![]() přístroje určíme z Ohmova zákona:
přístroje určíme z Ohmova zákona: ![]() .
Na základě Ohmova zákona můžeme také vnitřní odpor měřicího přístroje
změřit. U většiny přístrojů bývá vnitřní odpor uveden v manuálu nebo i přímo
na měřicím přístroji.
.
Na základě Ohmova zákona můžeme také vnitřní odpor měřicího přístroje
změřit. U většiny přístrojů bývá vnitřní odpor uveden v manuálu nebo i přímo
na měřicím přístroji.
![]() nejběžnější jsou následující způsoby převodu:
nejběžnější jsou následující způsoby převodu:
![]() .
Blokové schéma převodníku ukazuje obrázek. Po zadanou dobu
.
Blokové schéma převodníku ukazuje obrázek. Po zadanou dobu ![]() (první takt) se integruje měřené napětí
(první takt) se integruje měřené napětí ![]() . Hodnotě naintegrované
v druhém taktu je pak úměrný číselný údaj převodníku. Přesnost převodu je
dána stabilitou zdroje referenčního napětí
. Hodnotě naintegrované
v druhém taktu je pak úměrný číselný údaj převodníku. Přesnost převodu je
dána stabilitou zdroje referenčního napětí ![]() a v podstatě nezávisí
na časové stálosti rezistoru
a v podstatě nezávisí
na časové stálosti rezistoru ![]() , kapacitoru
, kapacitoru ![]() a zesílení
operačního zesilovače
a zesílení
operačního zesilovače ![]() , protože doba jednoho převodu je rovna zlomku
sekundy a po tuto dobu je možné udržet vlastnosti těchto součástek
stálé.
Před začátkem měření je sepnut spínač
, protože doba jednoho převodu je rovna zlomku
sekundy a po tuto dobu je možné udržet vlastnosti těchto součástek
stálé.
Před začátkem měření je sepnut spínač ![]() a tím vybit kapacitor
a tím vybit kapacitor ![]() .
V okamžiku začátku měření se rozpojí spínač
.
V okamžiku začátku měření se rozpojí spínač ![]() a spínač
a spínač ![]() připojí na integrátor měřené napětí
připojí na integrátor měřené napětí ![]() . Výstupní napětí integrátoru
. Výstupní napětí integrátoru
![]() lineárně roste. Současně se sepnutím spínače
lineárně roste. Současně se sepnutím spínače ![]() se
se otevře hradlo a čítač počítá impulzy o kmitočtu
se
se otevře hradlo a čítač počítá impulzy o kmitočtu ![]() . Jakmile se
čítač naplní, vydá impulz
. Jakmile se
čítač naplní, vydá impulz ![]() (naplnění trvá dobu
(naplnění trvá dobu ![]() ), obvod
řízení přepne spínač
), obvod
řízení přepne spínač ![]() na referenční napětí
na referenční napětí ![]() , jehož
polarita je opačná než
, jehož
polarita je opačná než ![]() . Současně s tím se znovu plní čítač a to
po tzv. přetečení na konci intervalu
. Současně s tím se znovu plní čítač a to
po tzv. přetečení na konci intervalu ![]() , protože hradlo zůstává
otevřeno. Výstupní napětí integrátoru klesá k nule. V okamžiku, kdy dosáhne
nuly, zareaguje napěťový komparátor
, protože hradlo zůstává
otevřeno. Výstupní napětí integrátoru klesá k nule. V okamžiku, kdy dosáhne
nuly, zareaguje napěťový komparátor ![]() a obvod řízení uzavře hradlo.
Tím končí druhý takt
a obvod řízení uzavře hradlo.
Tím končí druhý takt ![]() . Nový obsah čítače je přes dekodér přenesen na
zobrazovač a ukazuje změřené napětí. Poté je čítač vynulován signálem
. Nový obsah čítače je přes dekodér přenesen na
zobrazovač a ukazuje změřené napětí. Poté je čítač vynulován signálem
![]() a je vybit kapacitor
a je vybit kapacitor ![]() sepnutím spínače
sepnutím spínače ![]() a celý
cyklus se může opakovat.
Počet impulzů v čítači při vybíjení referenčním napětím je
a celý
cyklus se může opakovat.
Počet impulzů v čítači při vybíjení referenčním napětím je
![]() .
Pro vlastní integrátor platí:
.
Pro vlastní integrátor platí:
![\begin{picture}(100.10,100.10)
\put(19.79,20.02){\vector(1,0){80.31}}
\put(19....
...
\put(19.67,12.00){\makebox(0,0)[lt]{a) Ideální charakteristika}}
\end{picture}](img567.png)
![\begin{picture}(100.10,100.10)
\put(19.79,20.02){\vector(1,0){80.31}}
\put(19....
...
\put(20.67,11.50){\makebox(0,0)[lt]{c) Chyba zisku převodníku }}
\end{picture}](img568.png)
![\includegraphics[height=11cm, width=\textwidth, keepaspectratio=false]{ipc2}](img592.png)
![]() rozlišujeme rušení souhlasné
rozlišujeme rušení souhlasné ![]() (Common Mode) a sériové
(Common Mode) a sériové ![]() (Series Mode).
Souhlasné rušivé napětí
(Series Mode).
Souhlasné rušivé napětí ![]() působí ve stejné fázi na vstupních
svorkách H a L číslicového voltmetru a způsobuje rušivý proud
působí ve stejné fázi na vstupních
svorkách H a L číslicového voltmetru a způsobuje rušivý proud ![]() ,
který vytváří na rezistoru nevyvážených přívodů chybové napětí.
Sériové rušivé napětí
,
který vytváří na rezistoru nevyvážených přívodů chybové napětí.
Sériové rušivé napětí ![]() se přičítá přímo k měřenému napětí
se přičítá přímo k měřenému napětí ![]() .
Zdrojem stejnosměrného rušivého napětí jsou v provozu nejčastěji
termoelektrická napětí ve vstupním obvodu voltmetru a zbytková napětí přepínače
na vstupu voltmetru.
Zdrojem střídavého rušivého napětí je často napětí indukované do vstupních
obvodů multimetru elektromagnetickým polem síťových vodičů, nebo zvlněním
napětí napájecího zdroje.
Schopnost číslicového voltmetru potlačit souhlasné rušení je
charakterizována činitelem potlačení součtového rušení
.
Zdrojem stejnosměrného rušivého napětí jsou v provozu nejčastěji
termoelektrická napětí ve vstupním obvodu voltmetru a zbytková napětí přepínače
na vstupu voltmetru.
Zdrojem střídavého rušivého napětí je často napětí indukované do vstupních
obvodů multimetru elektromagnetickým polem síťových vodičů, nebo zvlněním
napětí napájecího zdroje.
Schopnost číslicového voltmetru potlačit souhlasné rušení je
charakterizována činitelem potlačení součtového rušení
