Subsections
Senzor [20] je funkční prvek tvořící vstupní blok měřicího řetězce, který je
v přímém styku s měřeným prostředím. Pojem senzor je ekvivalentní pojmu
snímač, převodník nebo detektor. Citlivá část senzoru se občas označuje
jako čidlo. Senzor jako primární zdroj informace snímá sledovanou fyzikální,
chemickou nebo biologickou veličinu a dle určitého definovaného principu ji
transformuje na měřicí veličinu - nejčastěji na veličinu elektrickou.
- Dle měřené veličiny:
senzory teploty, tlaku, průtoku, radiačních veličin, mechanických veličin
(posunutí, polohy, rychlosti atd.), senzory elektrických
a magnetických veličin atd.
- Dle fyzikálního principu:
senzory odporové, indukčnostní, indukční, kapacitní, magnetické, piezoelektrické,
optoelektronické, optické vláknové,chemické, biologické aj.
- Dle styku senzoru s měřeným prostředím:
bezdotykové, dotykové.
- Dle transformace signálu: aktivní, pasivní.
Aktivní senzor je senzor, který se působením snímané veličiny chová jako
zdroj elektrické energie.
Pasivní senzor je senzor, u kterého je nutné elektrickou veličinu
(odpor, indukčnost, kapacitu atd.) dále transformovat na analogový napěťový
nebo proudový signál. U pasivních senzorů je na rozdíl od aktivních senzorů
nezbytné napájení.
- Dle výrobní technologie:
elektromechanické, mechanické, pneumatické, elektrické, elektronické,
elektrochemické, polovodičové, mikroelektronikcé, optoelektroniké aj.
| Statické parametry |
Dynamické parametry |
| citlivost |
parametry časové odezvy |
| práh citlivosti |
časová konstanta |
| dynamický rozsah |
šíře frekvenčního pásma |
| reprodukovatelnost |
frekvenční rozsah |
| rozlišitelnost |
rychlost číslicového převodu |
| aditivní a multiplikativní chyby |
parametry šumu |
| linearita |
|
| parametry výstupu |
|
Statická převodní charakteristika senzoru je dána funkční závislosti
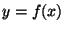 mezi vstupní veličinou
mezi vstupní veličinou 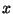 a výstupní veličinou
a výstupní veličinou 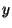 v časově ustáleném stavu.
v časově ustáleném stavu.
Tuto závislost lze velmi často popsat polynomem
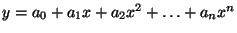 . Ideální statická
charakteristika je dána vztahem
. Ideální statická
charakteristika je dána vztahem 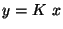 , kde
, kde  je citlivost
senzoru a současně konstanta přenosové funkce. Pro obecnou funkční závislost
je citlivost
je citlivost
senzoru a současně konstanta přenosové funkce. Pro obecnou funkční závislost
je citlivost  definována
definována
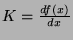 . Vzhledem k působení
parazitních veličin je lepší definovat citlivost takto:
. Vzhledem k působení
parazitních veličin je lepší definovat citlivost takto:
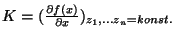 , kde
, kde
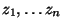 jsou parazitní veličiny.
jsou parazitní veličiny.
Práh citlivosti senzoru je dán hodnotou snímané veličiny, při níž
je na výstupu senzoru signál odpovídající střední kvadratické odchylce
šumu senzoru. Například pro napěťový signál je práh citlivosti
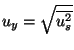
Dynamický rozsah senzoru je dán intervalem přípustných hodnot snímané
fyzikální veličiny, ohraničený práhem citlivosti a maximální hodnotou
měřené veličiny.
Reprodukovatelnost senzoru je dána odchylkou naměřených hodnot při
krátkodobém časovém sledu měření neměnné vstupní veličiny a neměnných
rušivých vlivů okolí.
Rozlišitelnost senzoru je nejmenší změna snímané veličiny odpovídající
absolutní nebo relativní chybě senzoru. Při analogové transforamci signálu je
rozlišitelnost dána vztahem
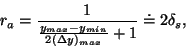 |
(106) |
kde
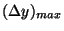 je maximální hodnota absolutní chyby měření v rozsahu
měření,
je maximální hodnota absolutní chyby měření v rozsahu
měření, 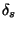 je relativní chyba senzoru.
je relativní chyba senzoru.
Relativní chyba senzoru je dána vztahem
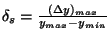 .
.
Poznámka: U senzorů se chyby často udávají vztažené ke vstupní veličině, tj.
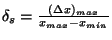 .
.
Aditivní a multiplikativní chyby viz. ....
Spolehlivost senzoru (přístroje)
Spolehlivost je podle ČSN IEC 50 (191) chápána jako souhrnný termín pro
popis pohotovosti a činitelů, kteří ovlivňují: bezporuchovost, udržovatelnost
a zajištěnost údržby. Pro měřicí přístroje je pak pro takto obecně chápanou
spolehlivost nejvýznamnější dílčí vlastností bezporuchovost, která je
definována jako schopnost objektu plnit požadovanou funkci v daných podmínkách
a v daném časovém období.
Ukazatelé bezporuchovosti obecně popisují pravděpodobnost chování náhodné velčiny
"doba do poruchy" (při stanovení kritéria poruchy). U přístrojů chápaných
jako neopravované objekty jsou pak nejčastěji používány tyto:
- pravděpodobnost bezporuchového provozu
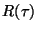
- pravděpodobnost poruchy
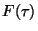
- hustota pravděpodobnosti poruch
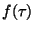
- intenzita poruch
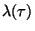
- střední doba mezi poruchami (MIBF)
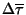
U přístrojů, které lze opravovat je používána následující charakteristika:
- střední doba do první poruchy (MITFF)
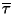
Pravděpodobnost poruchy 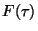 vyjadřuje, že během intervalu
vyjadřuje, že během intervalu
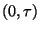 vznikne porucha u
vznikne porucha u 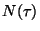 přístrojů z celkového sledovaného
počtu
přístrojů z celkového sledovaného
počtu 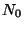 na začátku zkoušky, což lze vzjádřit vztahem
na začátku zkoušky, což lze vzjádřit vztahem
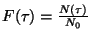 . Je zřejmé, že
. Je zřejmé, že
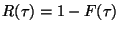 .
.
Hustota pravděpodobnosti poruch
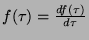 .
.
Intenzita poruch
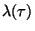 vyjadřuje rychlost vzniku poruch
v souboru sledovaných přístrojů
vyjadřuje rychlost vzniku poruch
v souboru sledovaných přístrojů 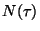 , u kterých ještě nenastala
porucha.
, u kterých ještě nenastala
porucha.
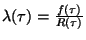
V případě konstantní intenzity poruch
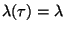 , tj. pro rozdělení náhodné veličiny
"doba do poruchy" platí exponenciální zákon, bude pravděpodobnost bezporuchového
provozu
, tj. pro rozdělení náhodné veličiny
"doba do poruchy" platí exponenciální zákon, bude pravděpodobnost bezporuchového
provozu 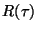 dána výrazem
dána výrazem
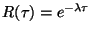
Většinou intenzita poruch klesá až do časového okamžiku 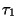 (období častých
poruch). Pak až do doby
(období častých
poruch). Pak až do doby 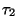 bývá intenzita poruch většinou konstantní.
Od časového okamžiku
bývá intenzita poruch většinou konstantní.
Od časového okamžiku 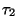 opět začíná závislost stoupat, protože se
začíná projevovat opotřebení atd.
opět začíná závislost stoupat, protože se
začíná projevovat opotřebení atd.
Střední doba do poruchy
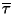 se zavádí u přístrojů, které
se při poruše neopravují; vyjadřuje aritmetický růměr dob bezporuchového
provozu
se zavádí u přístrojů, které
se při poruše neopravují; vyjadřuje aritmetický růměr dob bezporuchového
provozu 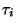 všech
všech 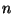 přístrojů zkoumaného souboru do vzniku první poruchy,
tedy
přístrojů zkoumaného souboru do vzniku první poruchy,
tedy
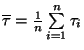 .
.
Střední doba mezi poruchami
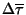 vyjadřuje
aritmetický průměr všech dob bezporuchového provozu
vyjadřuje
aritmetický průměr všech dob bezporuchového provozu 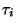 přístroje
mezi dvěma za sebou následujícími poruchami, tedy
přístroje
mezi dvěma za sebou následujícími poruchami, tedy
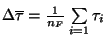 ,
kde
,
kde 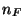 je celkový počet poruch jednoho přístroje. Určuje se u přístroje,
které se po poruše opravují, tj. obnovuje se jejich provozuschopnost.
je celkový počet poruch jednoho přístroje. Určuje se u přístroje,
které se po poruše opravují, tj. obnovuje se jejich provozuschopnost.
Měřená hodnota fyzikální nebo jiné veličiny se neustále mění s časem.
Senzory zařazené v regulačních smyčkách nebo indikující mezní stavy procesu musí být
navrženy tak, aby výstupní signál 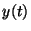 sledoval s minimálním zkreslením
vstupní signál
sledoval s minimálním zkreslením
vstupní signál 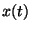 . V dalším budeme vycházet z předpokladu, že dynamické chování
senzoru lze popsat lineární diferenciální rovnicí s konstantními koeficienty.
Pokud rovnice neni lineární, je nutné ji po úsecích linearizovat a dynamické chování
sledovat v daných úsecích. Podrobný matematický popis problematiky je možné
nalézt v [20] a [22]. Graficky se zobrazují dynamické vlastnosti dynamickými
charakteristikami:
. V dalším budeme vycházet z předpokladu, že dynamické chování
senzoru lze popsat lineární diferenciální rovnicí s konstantními koeficienty.
Pokud rovnice neni lineární, je nutné ji po úsecích linearizovat a dynamické chování
sledovat v daných úsecích. Podrobný matematický popis problematiky je možné
nalézt v [20] a [22]. Graficky se zobrazují dynamické vlastnosti dynamickými
charakteristikami:
- Přechodová charakteristika - odezva na skokovou změnu vstupní
veličiny; popisuje ji přechodová funkce
- Rychlostní charakteristika - odezva na vstupní veličinu měnící se
konstantní rychlostí; popisuje ji rychlostní funkce
- Impulsní charakteristika - odezva na změnu vstupní veličiny
ve formě impulsu; popisuji ji impulsní funkce
- Frekvenční charakteristika - vyjádření chování přístroje při
harmonické změně vstupní veličiny; popisuje ji frekvenční přenosová funkce.
Průběh libovolné dynamické charakteristiky lze určit experimentálně, nebo
výpočtem.
Z hlediska chyb je nutné kromě systematických a nahodilých chyb jednotlivých
funkčních bloků senzoru uvažovat zapojení senzoru do systémum tj. musí
se respektovat vazba senozoru s ostatními částmi systému a parazitní
vazby uvnitř senzoru. Mezi rušivé veličiny prostředí patří například
teplota, tlak, vlhkost, radiace, pole (elektrické, magnetické,
elektromagnetické) aj. Zpětný vliv senzoru na měřený proces má za následek,
že hodnota měřené veličiny se změní vlivem senzoru (například dotykový
teploměr sníží teplotu měřeného místa). Jako zpětný vliv rozhraní, přístroje
a jiného zařízení připojeného k senzoru lze uvést zatěžovací impedance, rušivé
signály vedení nebo parazitními zemními smyčkami aj. Vnitřní rušení uvnitř
senzoru a případného elektronického řetězce je působeno oteplením, parazitními
kapacitami nebo jinými vazbami aj.
V praxi se můžeme setkat s celou řadou metod, které zmenšují chybu senzorů.
Podrobný popis metod je možné nalézt například v [22]. Zde uvádíme jen přehled
nejpoužívanejších metod:
- Metoda kompenzačního senozoru
- Metoda diferenčního senzoru
- Metoda zpětnovazebního senzoru
- Metoda sériového zapojení linearizačního členu
- Metoda linearizace při číslicovém zpracování signálu
- Metoda automatické kalibrace
- Metoda filtrace
- Metoda posunu spektra
- Metoda korekce dynamických chyb senzoru
© František Šťastný, 1997
![]() mezi vstupní veličinou
mezi vstupní veličinou ![]() a výstupní veličinou
a výstupní veličinou ![]() v časově ustáleném stavu.
v časově ustáleném stavu.
![]() . Ideální statická
charakteristika je dána vztahem
. Ideální statická
charakteristika je dána vztahem ![]() , kde
, kde ![]() je citlivost
senzoru a současně konstanta přenosové funkce. Pro obecnou funkční závislost
je citlivost
je citlivost
senzoru a současně konstanta přenosové funkce. Pro obecnou funkční závislost
je citlivost ![]() definována
definována
![]() . Vzhledem k působení
parazitních veličin je lepší definovat citlivost takto:
. Vzhledem k působení
parazitních veličin je lepší definovat citlivost takto:
![]() , kde
, kde
![]() jsou parazitní veličiny.
jsou parazitní veličiny.
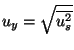
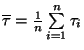 .
.
![]() sledoval s minimálním zkreslením
vstupní signál
sledoval s minimálním zkreslením
vstupní signál ![]() . V dalším budeme vycházet z předpokladu, že dynamické chování
senzoru lze popsat lineární diferenciální rovnicí s konstantními koeficienty.
Pokud rovnice neni lineární, je nutné ji po úsecích linearizovat a dynamické chování
sledovat v daných úsecích. Podrobný matematický popis problematiky je možné
nalézt v [20] a [22]. Graficky se zobrazují dynamické vlastnosti dynamickými
charakteristikami:
. V dalším budeme vycházet z předpokladu, že dynamické chování
senzoru lze popsat lineární diferenciální rovnicí s konstantními koeficienty.
Pokud rovnice neni lineární, je nutné ji po úsecích linearizovat a dynamické chování
sledovat v daných úsecích. Podrobný matematický popis problematiky je možné
nalézt v [20] a [22]. Graficky se zobrazují dynamické vlastnosti dynamickými
charakteristikami: