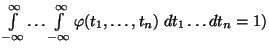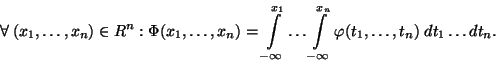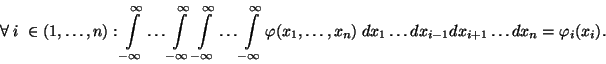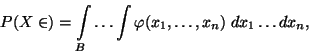Subsections
Další podrobnosti o nahodných vektorech naleznete například v [14].
Zde uvedeme jen základní definice.
Nechť
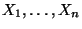 jsou náhodné veličiny,
jsou náhodné veličiny,
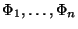 jejich
distribuční funkce (resp.
jejich
distribuční funkce (resp.
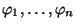 hustoty
pravděpodobnosti ve spojitém případě resp.
hustoty
pravděpodobnosti ve spojitém případě resp.
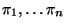 pravděpodobnostní
funkce v diskrétním případě).
pravděpodobnostní
funkce v diskrétním případě).
Náhodný vektor je uspořádaná n-tice
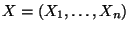 .
Jeho distribuční funkci definujeme vztahem:
.
Jeho distribuční funkci definujeme vztahem:
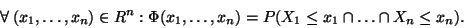 |
(17) |
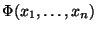 má anlogické vlastnosti jako distribuční funkce
skalární náhodné veličiny: speciálně je neklesající a zprava spojitá
vzhledem ke každé jednotlivé proměnné, dale
má anlogické vlastnosti jako distribuční funkce
skalární náhodné veličiny: speciálně je neklesající a zprava spojitá
vzhledem ke každé jednotlivé proměnné, dale
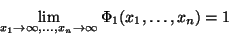 |
(18) |
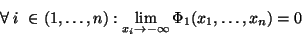 |
(19) |
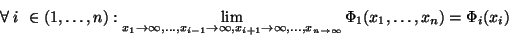 |
(20) |
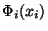 se v této souvislosti nazývá marginální distribuční funkce
náhodné veličiny
se v této souvislosti nazývá marginální distribuční funkce
náhodné veličiny 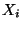 a
a
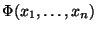 se nazývá simultánní
distribuční funkce náhodné vekoru X.
se nazývá simultánní
distribuční funkce náhodné vekoru X.
Náhodný vektor
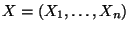 se nazývá diskrétní, právě když
existuje funkce
se nazývá diskrétní, právě když
existuje funkce
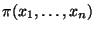 , která je nulová v
, která je nulová v 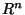 s výjimkou
nejméně jednoho a nejvýše spočetně mnoha bodů, kde je kladná
s výjimkou
nejméně jednoho a nejvýše spočetně mnoha bodů, kde je kladná
(pro všechna
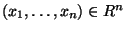 :
:
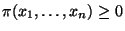 ),
je normovaná
),
je normovaná
(
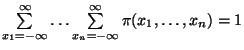 )
a platí pro ni:
)
a platí pro ni:
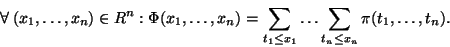 |
(21) |
Funkce
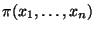 se nazývá pravděpodobnostní funkce
diskrétního náhodného vektoru
se nazývá pravděpodobnostní funkce
diskrétního náhodného vektoru 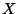 .
.
Pro pravděpodobnostní funkci dále platí:
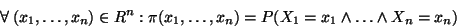 |
(22) |
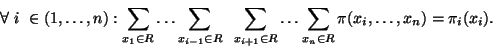 |
(23) |
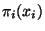 se nazývá marginální pravděpodobnostní funkce
náhodné veličiny
se nazývá marginální pravděpodobnostní funkce
náhodné veličiny 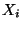 a
a
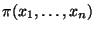 simultánní pravděpodobnostní funkce náhodného vektoru
simultánní pravděpodobnostní funkce náhodného vektoru 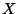 .
Pravděpodobnost, že náhodný vektor
.
Pravděpodobnost, že náhodný vektor
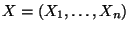 se bude
realizovat v oblasti
se bude
realizovat v oblasti
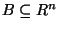 , se vypočte podle vzorce
, se vypočte podle vzorce
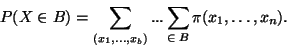 |
(24) |
Náhodný vektor
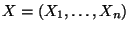 se nazývá spojitý, právě když existuje
po částech spojitá nezáporná funkce
se nazývá spojitý, právě když existuje
po částech spojitá nezáporná funkce
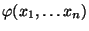 (vlastnost S1: pro všechna
(vlastnost S1: pro všechna
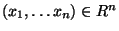 :
:
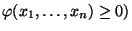 , která je normovaná
, která je normovaná
(vlastnost S2:
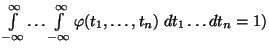
a platí pro ni
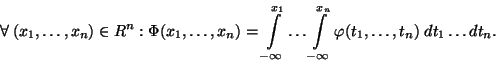 |
(25) |
Funkce
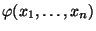 se nazývá hustota pravděpodobnosti
spojitého náhodného vektoru
se nazývá hustota pravděpodobnosti
spojitého náhodného vektoru 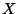 .
Pro hustotu pravděpodobnosti dále platí:
.
Pro hustotu pravděpodobnosti dále platí:
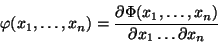 |
(26) |
ve všech bodech spojitosti funkce
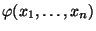 .
.
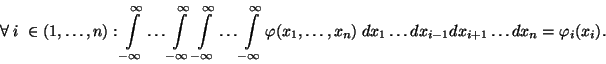 |
(27) |
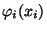 se nazývá marginální hustota náhodné veličiny
se nazývá marginální hustota náhodné veličiny 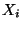 a
a
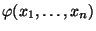 simultánní hustota náhodného vektoru
simultánní hustota náhodného vektoru 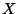 .
Pravděpodobnost, že náhodný vektor
.
Pravděpodobnost, že náhodný vektor
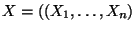 se bude ralizovat
v oblasti
se bude ralizovat
v oblasti
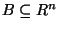 , se vypočte podle vzorce
, se vypočte podle vzorce
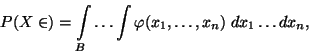 |
(28) |
pokud integrál vpravo existuje.
Příklad: Nezávisle na sobě hodíme dvěma kostkami. Náhodná veličina 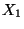 udává počet ok, která padla na první kostce a náhodná veličina
udává počet ok, která padla na první kostce a náhodná veličina 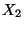 udává maximum z počtu ok, která padla na obou kostkách.
Najděte simultánní pravděpodobnostní funkci
udává maximum z počtu ok, která padla na obou kostkách.
Najděte simultánní pravděpodobnostní funkci 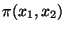 a obě marginální pravděpodobnostní funkce
a obě marginální pravděpodobnostní funkce 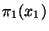 a
a 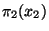 .
.
Příklad Nechť je dán systém složený ze dvou bloků.
Pravděpodobnost, že i-tý blok správně funguje je 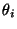 ,
,
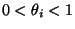 pro
pro 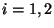 a pravděpodobnost, že správně
fungují oba bloky je
a pravděpodobnost, že správně
fungují oba bloky je 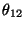 ,
,
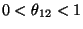 . Nechť
náhodná veličina
. Nechť
náhodná veličina 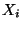 je ukazatel fungování i-tého bloku, i=1,2.
Vyjádřete pravděpodobnostní funkci
je ukazatel fungování i-tého bloku, i=1,2.
Vyjádřete pravděpodobnostní funkci 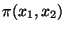 náhodněho vektoru
náhodněho vektoru
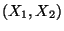 a obě marginální pravděpodobnostní funkce
a obě marginální pravděpodobnostní funkce 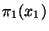 a
a 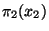 .
.
© František Šťastný, 1997
![]() jsou náhodné veličiny,
jsou náhodné veličiny,
![]() jejich
distribuční funkce (resp.
jejich
distribuční funkce (resp.
![]() hustoty
pravděpodobnosti ve spojitém případě resp.
hustoty
pravděpodobnosti ve spojitém případě resp.
![]() pravděpodobnostní
funkce v diskrétním případě).
pravděpodobnostní
funkce v diskrétním případě).
![]() .
Jeho distribuční funkci definujeme vztahem:
.
Jeho distribuční funkci definujeme vztahem:
![]() se nazývá diskrétní, právě když
existuje funkce
se nazývá diskrétní, právě když
existuje funkce
![]() , která je nulová v
, která je nulová v ![]() s výjimkou
nejméně jednoho a nejvýše spočetně mnoha bodů, kde je kladná
s výjimkou
nejméně jednoho a nejvýše spočetně mnoha bodů, kde je kladná
![]() :
:
![]() ),
je normovaná
),
je normovaná
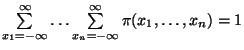 )
a platí pro ni:
)
a platí pro ni:
![]() se nazývá spojitý, právě když existuje
po částech spojitá nezáporná funkce
se nazývá spojitý, právě když existuje
po částech spojitá nezáporná funkce
![]() (vlastnost S1: pro všechna
(vlastnost S1: pro všechna
![]() :
:
![]() , která je normovaná
, která je normovaná