Subsections
Obrázek:
Graf normálního rozdělení pro různé hodnoty 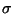
|
|
Normální rozdělení (Gaussovo rozdělení) je nejznámější model rozdělení
spojité náhodné veličiny,
používaný v technické praxi. Při opakovaném měření téže veličiny za stejných
podmínek způsobují náhodné, nekontrolovatelné vlivy odchylky od skutečné
měřené veličiny
DEFINICE: Normovaným normálním rozdělením nazýváme normální rozdělení,
které má
střední hodnotu 0 a rozptyl 1. Jeho hustota 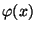 a distribuční
funkce
a distribuční
funkce 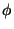 (x) jsou
(x) jsou
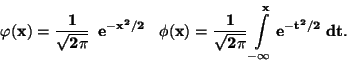 |
(9) |
DEFINICE: Obecným normálním rozdělením, stručně normálním rozdělením
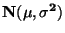 , nazýváme normální rozdělení se střední hodnotou
, nazýváme normální rozdělení se střední hodnotou
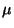 , rozptylem
, rozptylem 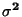 , hustotou
, hustotou
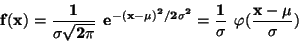 |
(10) |
a distribuční funkci
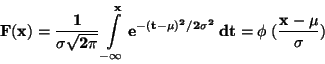 |
(11) |
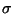 je tzv. směrodatná odchylka.
Má-li náhodná veličina normální rozdělení se známou střední hodnotou
je tzv. směrodatná odchylka.
Má-li náhodná veličina normální rozdělení se známou střední hodnotou
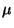 a směrodatnou odchylkou
a směrodatnou odchylkou 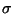 . Pak
. Pak
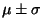 určuje interval,
ve kterém leží 68% měřených hodnot (základ pro zavedení střední kvadratické
chyby měření),
určuje interval,
ve kterém leží 68% měřených hodnot (základ pro zavedení střední kvadratické
chyby měření),
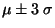 určuje interval,
ve které leží 99% měřených hodnot (základ pro určení krajní chyby měření).
určuje interval,
ve které leží 99% měřených hodnot (základ pro určení krajní chyby měření).
Poznámka: Dostupné modely v systému FAMULUS 3.5
NORM1.FM: graf hustoty a distribuční funkce normálního rozdělení
NORM2.FM: kreslí grafy normálního rozdělení pro různé hodnoty směrodatné
odchylky
MORM3.FM:kreslí grafy normálního rozdělení pro různé hodnoty střední hodnoty
NORM4.FM:zobrazuje interval spolehlivosti pro normální rozdělení
Obrázek:
Graf Studentova rozdělení
|
|
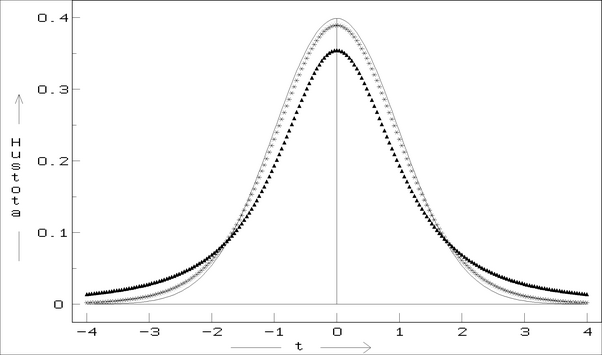
Obrázek:
Srovnání normálního rozdělení (plná čára) se Studentovým rozdělením:
trojúhelníky v=2; hvězdičky v=10; body v=20
|
|
Obrázek:
Poissonovo rozdělení
|
|
DEFINICE: GAMA funkce
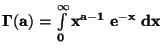 ,
kde
,
kde 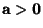 .
.
DEFINICE: STUDENTOVO rozdělení 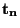 má hustotu
má hustotu
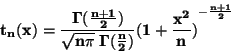 |
(12) |
Věta: Nechť
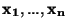 je výběr z normálního rozdělení
je výběr z normálního rozdělení
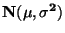 . Pak náhodná veličina
. Pak náhodná veličina
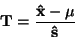 |
(13) |
má Studentovo rozdělení 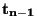 .
.
Poznámka: Dostupné modely v systému FAMULUS 3.5
GAMA.FM: Graf gama funkce pro 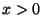
GAMA1.FM: Graf gama funkce pro kladné i záporné hodnoty x
STUDENT.FM: Srovnání Studentova rozdělení s normálním rozdělením
STUDB.FM: Interval spolehlivosti pro Studentovo rozdělení
Poissonovo rozdělení pravděpodobnosti má náhodná veličina, která vyjadřuje
počet výskytů málo pravděpodobných, řídkých jevů v určitém časovém, resp.
objemovém intervalu.
Například počet pulsů registrovaných GM-trubicí za zvolený časový interval.
Pravděpodobnostní funkce 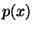 je definována vztahem:
je definována vztahem:
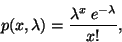 |
(14) |
kde 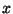 diskrétní náhodná veličina, nabývající pouze celočíselných hodnot
diskrétní náhodná veličina, nabývající pouze celočíselných hodnot
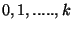 a
a 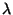 je parametr. Snadno lze dokázat, že střední
hodnota
je parametr. Snadno lze dokázat, že střední
hodnota
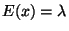 a také rozptyl
a také rozptyl
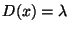 . Parametr
. Parametr 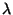 charakterizuje jak polohu, tak i rozptýlení
charakterizuje jak polohu, tak i rozptýlení
Náhodná veličina 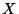 má rovnoměrné rozdělení, jestliže má hustotu pravděpodobnosti
má rovnoměrné rozdělení, jestliže má hustotu pravděpodobnosti
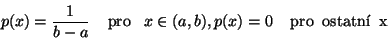 |
(15) |
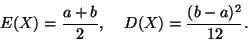 |
(16) |
=rov.pic
;''
© František Šťastný, 1997
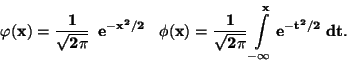
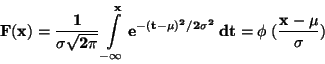
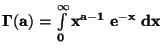 ,
kde
,
kde 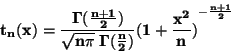
![]() je definována vztahem:
je definována vztahem:
![]() má rovnoměrné rozdělení, jestliže má hustotu pravděpodobnosti
má rovnoměrné rozdělení, jestliže má hustotu pravděpodobnosti