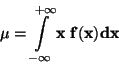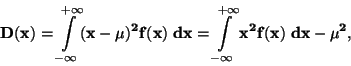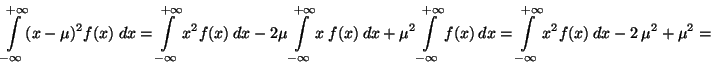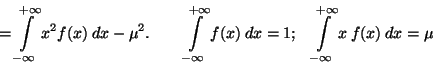DEFINICE: Zákon rozdělení náhodné veličiny 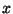 je zákon, který udává
pravděpodobnosti
jevů, které lze touto veličinou popsat, např. jevů
je zákon, který udává
pravděpodobnosti
jevů, které lze touto veličinou popsat, např. jevů 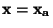 nebo
nebo
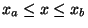 atd.
atd.
DEFINICE: Diskrétní náhodné veličiny jsou veličiny, které nabývají jen
konečně nebo
spočetně mnoha hodnot např. 0,1,2,... Jejich zákon rozdělení,
který také
nazýváme diskrétním, je zcela popsán pravděpodobnostmi jednotlivých hodnot
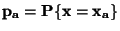 .
.
DEFINICE: Spojité náhodné veličiny jsou veličiny, které mají tzv. spojitý
zákon
rozdělení, který je zcela popsán hustotou pravděpodobnosti nebo stručně jen
hustotou
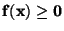 , jejíž integrací dostaneme pravděpodobnost, že
náhodná veličina padne do intervalu
, jejíž integrací dostaneme pravděpodobnost, že
náhodná veličina padne do intervalu
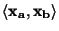 :
:
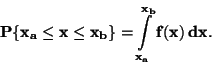 |
(1) |
Je-li 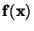 spojitá vyjadřuje
spojitá vyjadřuje 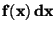 pravděpodobnost,
že náhodná veličina padne do intervalu
pravděpodobnost,
že náhodná veličina padne do intervalu
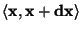 .
.
Obrázek:
Graf rozdělení pravděpodobnosti pro diskrétní náhodnou veličinu
|
|
Obrázek:
Graf distribuční funkce pro diskrétní náhodnou veličinu z předcházejícího obrázku
|
|
DEFINICE:
Distribuční funkce 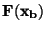 náhodné veličiny
náhodné veličiny 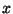 je
funkcí, která udává
pro každé
je
funkcí, která udává
pro každé 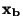 pravděpodobnost nerovnosti
pravděpodobnost nerovnosti 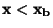 .
Pro diskrétní
náhodné veličiny je
.
Pro diskrétní
náhodné veličiny je
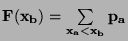 , kde
, kde
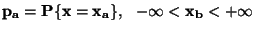 .
.
Pro spojité náhodné veličiny je
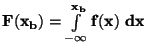 .
Pro spojité náhodné veličiny tedy platí
.
Pro spojité náhodné veličiny tedy platí
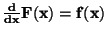 .
.
DEFINICE: Střední hodnota
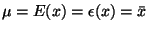 diskrétní náhodné veličiny x je definována takto:
diskrétní náhodné veličiny x je definována takto:
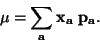 |
(2) |
Pro spojité náhodné veličiny :
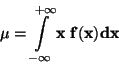 |
(3) |
DEFINICE: Rozptyl diskrétní náhodné veličiny je definován :
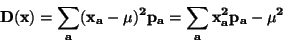 |
(4) |
Pro spojité náhodné veličiny
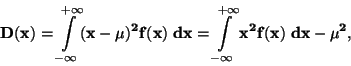 |
(5) |
kde 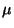 je střední hodnota.
je střední hodnota.
Příklad: Dokažte předcházející vztah:
Věta: Lineární funkce
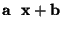 náhodné veličiny
náhodné veličiny 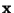 má tuto střední
hodnotu a rozptyl:
má tuto střední
hodnotu a rozptyl:
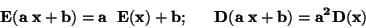 |
(6) |
Poznámka: Při analýze funkce náhodných veličin je třeba mít na paměti, že
každá nelineární transformace náhodné veličiny zkreslí její rozdělení a změní
i závislost rozptylu na střední hodnotě. I v případě, že má měřená veličina
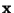 konstantní rozptyl
konstantní rozptyl 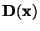 výsledky analýzy
výsledky analýzy 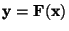 má již
rozptyl nekonstantní, pro který přibližně platí
má již
rozptyl nekonstantní, pro který přibližně platí
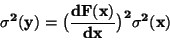 |
(7) |
Navíc platí, že střední hodnotu 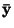 nelze určit přímo dosazením
nelze určit přímo dosazením
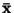 do funkce
do funkce 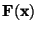 ,
,
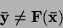 |
(8) |
Obrázek:
Hustota pravděpodobnosti pro spojitou náhodnou veličinu
|
|
Obrázek:
Distribuční funkce pro spojitou náhodnou veličinu z předcházejícího obrázku
|
|
© František Šťastný, 1997
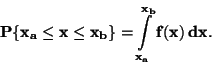
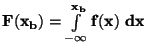 .
Pro spojité náhodné veličiny tedy platí
.
Pro spojité náhodné veličiny tedy platí