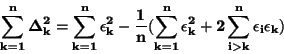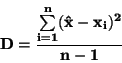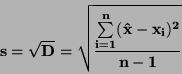V praxi většinou neznáme rozdělení náhodné veličiny, kterou zkoumáme.
V jednodušších případech známe alespoň typ rozdělení a zbývá určit jen
parametry, které je charakterizují. Například při zkoumání nahodilých
chyb ve fyzice většinou předpokládáme, že zkoumaná veličina má normální
rozdělení a provádíme statistický odhad střední hodnoty a rozptylu.
Při tom postupujeme tak, že opakovaným měřením za týchž podmínek získáme
náhodný výběr hodnot
 z možných výsledků měření.
Aritmetický průměr:
z možných výsledků měření.
Aritmetický průměr:
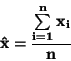 |
(29) |
Výběrový rozptyl okolo střední hodnoty:
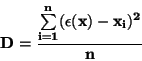 |
(30) |
Určení rozptylu D (vyloučení střední hodnoty, kterou neznáme):
Protože neznáme 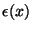 postupujeme takto: označíme
postupujeme takto: označíme
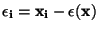 a
a
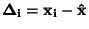 .
.
Vzájemným odečtením obou posledních rovnic dostaneme
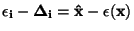 .
.
Sečtením přes všechna i dostaneme
Protože platí
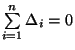 je možné poslední
rovnici upravit takto
je možné poslední
rovnici upravit takto
Umocněním poslední rovnice a sečtením přes všechna k dostaneme
Zanedbáme-li v závorce výraz s
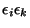 ,
v němž sčítáme jak kladná,
tak záporná čísla, dostaneme vztah pro výběrový rozptyl
,
v němž sčítáme jak kladná,
tak záporná čísla, dostaneme vztah pro výběrový rozptyl
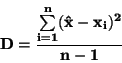 |
(31) |
Častěji než rozptyl se používá standardní (směrodatná) odchylka
s jednoho měření
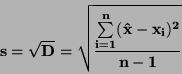 |
(32) |
© František Šťastný, 1997
![]() z možných výsledků měření.
Aritmetický průměr:
z možných výsledků měření.
Aritmetický průměr:
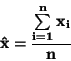
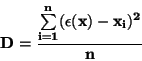
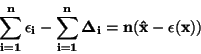
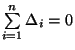 je možné poslední
rovnici upravit takto
je možné poslední
rovnici upravit takto