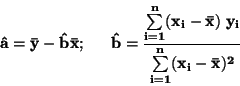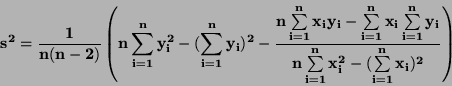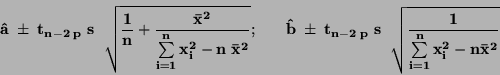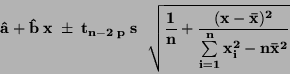Subsections
Interpolace a aproximace funkcí nebo experimentálních dat zahrnuje řadu
technik.
Obecně se provádí náhradou funkce 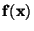 , zadané hodnotami
, zadané hodnotami
![$\bf [x_i, y_i], i= 1, 2,....., n$](img335.png) vhodnou aproximující funkcí
vhodnou aproximující funkcí 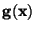 .
Za aproximující funkci
.
Za aproximující funkci 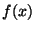 se často volí lineární kombinace
elementárních funkcí
se často volí lineární kombinace
elementárních funkcí 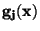 .
.
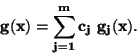 |
(61) |
Příkladem elementárních funkcí 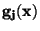 jsou polynomy
jsou polynomy 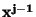 racionální funkce, podíly polynomů, trigonometrické funkce,
exponenciální funkce atd. Aproximující funkce souvisí se zadáním dané úlohy
a ovlivňují stupeň aproximace. Ten se obyčejně vyjadřuje jako vzdálenost
mezi aproximující funkcí
racionální funkce, podíly polynomů, trigonometrické funkce,
exponenciální funkce atd. Aproximující funkce souvisí se zadáním dané úlohy
a ovlivňují stupeň aproximace. Ten se obyčejně vyjadřuje jako vzdálenost
mezi aproximující funkcí 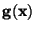 a aproximovanou funkci
a aproximovanou funkci 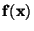 , resp.
diskrétními hodnotami
, resp.
diskrétními hodnotami 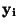 .
Zvláštním případem aproximace je interpolace: při interpolaci závislostí
se sestrojuje funkce
.
Zvláštním případem aproximace je interpolace: při interpolaci závislostí
se sestrojuje funkce 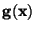 tak, aby procházela zadanými body
tak, aby procházela zadanými body
![$\bf [x_i, y_i], i= 1, 2,....., n$](img335.png) , a splňovala přitom podmínky týkající se jejího
tvaru.
Při interpolaci funkcí musí být v definovaných bodech
, a splňovala přitom podmínky týkající se jejího
tvaru.
Při interpolaci funkcí musí být v definovaných bodech 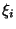
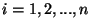 nazvaných uzlové body interpolace, funkce
nazvaných uzlové body interpolace, funkce 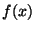 a
a 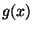 spojité ve funkčních hodnotách a hodnotách zvolených derivací
spojité ve funkčních hodnotách a hodnotách zvolených derivací
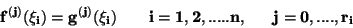 |
(62) |
Zde 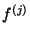 označuje j-tou derivaci a
označuje j-tou derivaci a 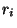 je maximální derivací v i-tém
uzlu, ve které jsou totožné obě, aproximovaná a aproximující funkce.
Interpolace se v technické praxi využívá pro
je maximální derivací v i-tém
uzlu, ve které jsou totožné obě, aproximovaná a aproximující funkce.
Interpolace se v technické praxi využívá pro
- Zespojitění tabelárních údajů
- Náhradu složitých funkcí
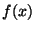 nebo funkcí, které nelze přímo
vyčíslit
nebo funkcí, které nelze přímo
vyčíslit
- Numerickou derivaci a integraci
- Kreslení grafů závislostí zadaných tabulkou
Při aproximaci závislostí se předpokládá aditivní působení chyb typu
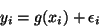 |
(63) |
Pokud je druh funkce 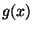 předem znám, přechází úloha aproximace na úlohu
lineární nebo nelineární regrese. Pokud se volí
předem znám, přechází úloha aproximace na úlohu
lineární nebo nelineární regrese. Pokud se volí 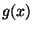 ve tvaru lineární
kombinace elementárních funkcí, jde o úlohu lineární regrese.
Aproximace se v technické praxi používá k:
ve tvaru lineární
kombinace elementárních funkcí, jde o úlohu lineární regrese.
Aproximace se v technické praxi používá k:
- Vyhlazování závislostí, tj. k eliminaci náhodných chyb
- Náhrada rozsáhlých souborů dat hladkými křivkami.
- Numerické derivování a integraci
- Tvorbě speciálních empirických modelů regresního typu jako je
splineregrese.
Mezi nejznámější postupy patří polynomická interpolace, která hledá polynom
g(x) nejmenšího možného stupně, splňující podmínku (62)
Tato úloha má právě jedno řešení a hledaný polynom je stupně nejvýše:
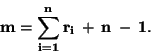 |
(64) |
Pokud je požadavkem shoda pouze ve funkčních hodnotách, jsou
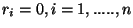 , a n-tice bodů je interpolována jednoznačně polynomem
(n - 1)ního stupně. Z podmínek (62) se
sestaví
, a n-tice bodů je interpolována jednoznačně polynomem
(n - 1)ního stupně. Z podmínek (62) se
sestaví 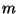 lineárních rovnic, ze
kterých se vypočtou odpovídající koeficienty
lineárních rovnic, ze
kterých se vypočtou odpovídající koeficienty 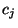 .
Pro větší počty uzlových bodů je výpočet koeficientů interpolačního polynomu
výše uvedenou metodou nepohodlný. Užívá se proto rozličných interpolačních
vzorců.
.
Pro větší počty uzlových bodů je výpočet koeficientů interpolačního polynomu
výše uvedenou metodou nepohodlný. Užívá se proto rozličných interpolačních
vzorců.
Formule se užívají pro případ 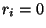 , kdy se konstruuje polynom stupně
nejvýše
, kdy se konstruuje polynom stupně
nejvýše 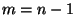 , interpolující
, interpolující 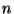 uzlových bodů, a kdy platí
uzlových bodů, a kdy platí
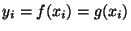 . Interpolační polynom splňující tyto podmínky lze
vyjádřit jako lineární kombinaci všech y-ových hodnot
. Interpolační polynom splňující tyto podmínky lze
vyjádřit jako lineární kombinaci všech y-ových hodnot
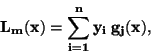 |
(65) |
kde 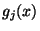 jsou polynomy stupně (n - 1) takové, že pro všechna j různá od
i platí
jsou polynomy stupně (n - 1) takové, že pro všechna j různá od
i platí
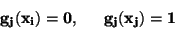 |
(66) |
Lagrangeův interpolační polynom má tvar:
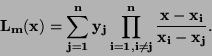 |
(67) |
Další podrobnosti je možné nalézt například v ![$[6]$](img178.png) .
Nevýhodou tradičního vyjádření interpolačního polynomu v Lagrangerově
tvaru je nutnost opětovného přepočítání všech členů při přidání dalšího bodu
.
Nevýhodou tradičního vyjádření interpolačního polynomu v Lagrangerově
tvaru je nutnost opětovného přepočítání všech členů při přidání dalšího bodu
 . Z tohoto hlediska je při postupném přidávání uzlů výhodnější
Newtonova interpolační formule
. Z tohoto hlediska je při postupném přidávání uzlů výhodnější
Newtonova interpolační formule
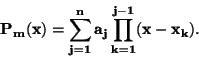 |
(68) |
Přidání bodu
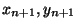 pak vede k interpolačnímu polynomu
pak vede k interpolačnímu polynomu
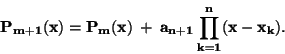 |
(69) |
Podrobný návod k výpočtu koeficientů 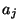 naleznete například v
naleznete například v ![$[6]$](img178.png) .
.
Při této interpolaci se požaduje, aby interpolační polynom 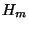 se svou první
derivací souhlasil ve všech uzlových bodech s danou funkcí a její první
derivací. To znamená, že
se svou první
derivací souhlasil ve všech uzlových bodech s danou funkcí a její první
derivací. To znamená, že
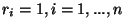 a interpolační polynom
je stupně
a interpolační polynom
je stupně 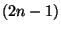 . Podrobnosti naleznete opět v
. Podrobnosti naleznete opět v ![$[6]$](img178.png) .
.
Při této aproximaci je interpolující funkce
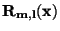 definována jako podíl
polynomu stupně
definována jako podíl
polynomu stupně 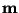 (v čitateli) a polynomu stupně
(v čitateli) a polynomu stupně 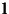 (ve jmenovateli).
(ve jmenovateli).
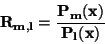 |
(70) |
Tato aproximace nahrazuje klasickou polynomickou interpolaci stupně (m + 1).
Podrobnosti jsou například v ![$[6]$](img178.png) .
.
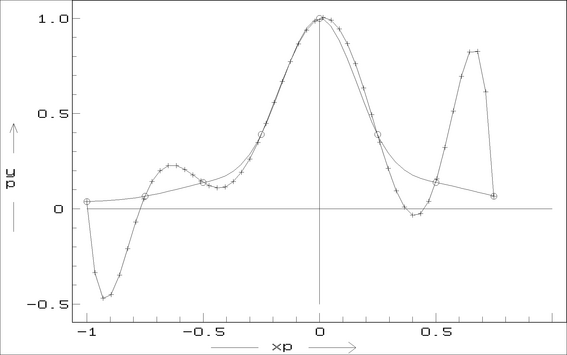
Obrázek:
Ukázka nevhodného použití interpolace polynomem (křížky), zadané body zobrazeny kroužky,
spojitě nakreslen skutečný průběh funkce
|
|
Obrázek:
Ukázka použití spline interpolace (spojitá křivka), zadané body
zobrazeny kroužky, průběh označený křížky ukazuje pro srovnaní interpolaci polynomem
|
|
Užívání polynomiálních interpolačních formulí má řadu nevýhod. Jsou totiž
složeny z elementárních funkcí definovaných na celé reálné ose, což vede
u interpolačních formulí vyšších řádů ke vzniku řady lokálních minim, maxim
a inflexních bodů, které neodpovídají průběhu funkce 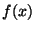 či tabelované
závislosti
či tabelované
závislosti
![$[x_i, y_i], i=1,....n$](img370.png) . Při interpolaci fyzikálních závislostí
se stává, že chování v jistém intervalu se výrazně liší od jejich chování
v intervalech sousedních. Jde o závislost tzv. neasociativní povahy. Z těchto
úvah plyne, že pro účely interpolace, ale i aproximace bude výhodnější
volit lokálně definované funkce, které budou v místech vzájemného styku, tj.
v uzlech, spojité ve funkčních hodnotách a v hodnotách zadaných derivací.
Vhodné interpolační funkce tohoto typu jsou složeny z polynomických úseků
a platí pro ně, že jsou ze třídy
. Při interpolaci fyzikálních závislostí
se stává, že chování v jistém intervalu se výrazně liší od jejich chování
v intervalech sousedních. Jde o závislost tzv. neasociativní povahy. Z těchto
úvah plyne, že pro účely interpolace, ale i aproximace bude výhodnější
volit lokálně definované funkce, které budou v místech vzájemného styku, tj.
v uzlech, spojité ve funkčních hodnotách a v hodnotách zadaných derivací.
Vhodné interpolační funkce tohoto typu jsou složeny z polynomických úseků
a platí pro ně, že jsou ze třídy ![$C^m[a, b]$](img371.png) . Obecně jsou funkce třídy
. Obecně jsou funkce třídy
![$C^m[a, b]$](img371.png) na intervalu
na intervalu ![$[a, b]$](img372.png) spojité v prvních m derivacích a funkčních
hodnotách.
S využitím uvedených vlastností funkcí ze třídy
spojité v prvních m derivacích a funkčních
hodnotách.
S využitím uvedených vlastností funkcí ze třídy ![$C^m[a, b]$](img371.png) můžeme definovat
obecně polynomický spline
můžeme definovat
obecně polynomický spline 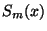 s uzly
s uzly
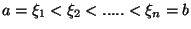 .
Tento spline je na každém úseku
.
Tento spline je na každém úseku
![$[\xi_j, \xi_{j+1}], j = 1, ....,n-1$](img375.png) ,
reprezentován polynomem maximálně m-tého stupně. Pokud je v nějakém bodě
,
reprezentován polynomem maximálně m-tého stupně. Pokud je v nějakém bodě 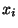 některá derivace
některá derivace
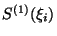 nespojitá, jde o defektní spline.
nespojitá, jde o defektní spline.
Vlastnosti spline 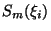 závisí na:
závisí na:
- řádu polynomu m, přičemž se obvykle volí kubický spline (m = 3)
- počtu a polohách uzlů
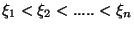
- defektech v uzlových bodech
Formulace problému: K hodnotám
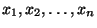 nezávisle proměnné
získáme měřením odpovídající hodnoty závisle proměnné
nezávisle proměnné
získáme měřením odpovídající hodnoty závisle proměnné
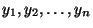 .
Tyto hodnoty nesplňují regresní model přesně, ale jsou zatíženy chybami.
Například pro lineární regresy je možno psát:
.
Tyto hodnoty nesplňují regresní model přesně, ale jsou zatíženy chybami.
Například pro lineární regresy je možno psát:
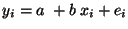 ,
kde
,
kde 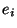 jsou chyby.
jsou chyby.
Musí být splněny následující předpoklady:
- Chyby mají nulovou střední hodnotu.
- Chyby jsou vzájemně nezávislé.
- Chyby mají normální rozdělení.
- Chyby mají stejný (neznámý) rozptyl.
- Nezávislé proměnné jsou lineárně nezávislé, žádnou tedy není možné
nahradit lineární kombinací zbývajících.
- Na regresní koeficienty již nejsou kladena žádná další omezení
(například nezápornost regresních koeficientů atd.)
- Nezávisle proměnné (často se užívá i název vysvětlující proměnné) jsou
nenáhodné, tzn. nejsou výsledkem žádného experimentu.
Lineární model splňující tyto předpoklady patří do třídy klasických
lineárních modelů. Nejdůležitější jsou první tři předpoklady. Nesplnění
posledních tří předpokladů se řeší zavedením zobecněného modelu lineární
regrese
Dále použijeme následující označení:
 - hladina spolehlivosti (je-li například
- hladina spolehlivosti (je-li například 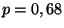 , pak existuje
68 % pravděpodobnost, že hodnota veličiny leží ve vymezeném intervalu).
, pak existuje
68 % pravděpodobnost, že hodnota veličiny leží ve vymezeném intervalu).
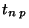 - Studentův koeficient odpovídající
- Studentův koeficient odpovídající 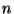 stupňů volnosti
a pravděpodobnosti
stupňů volnosti
a pravděpodobnosti 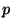 .
.
MODEL:
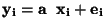
Odhad regresního koeficientu 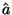 a odhad rozptylu
a odhad rozptylu 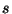 :
:
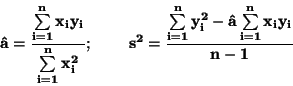 |
(71) |
Interval spolehlivosti pro regresní koeficient:
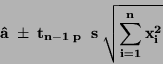 |
(72) |
Interval spolehlivosti pro vyrovnávanou hodnotu:
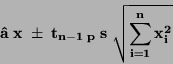 |
(73) |
MODEL:
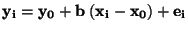
Odhad regresního koeficientu 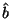 a odhad rozptylu
a odhad rozptylu 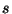 :
:
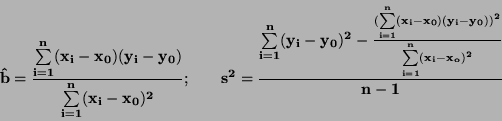 |
(74) |
Interval spolehlivosti pro regresní koeficient:
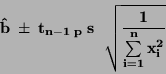 |
(75) |
Interval spolehlivosti pro vyrovnávanou hodnotu:
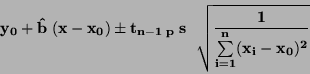 |
(76) |
MODEL:
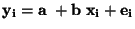
Odhad regresních koeficientů:
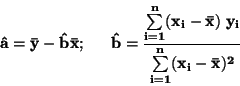 |
(77) |
Odhad rozptylu:
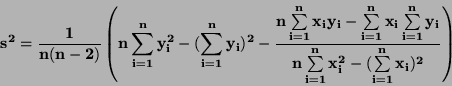 |
(78) |
Interval spolehlivosti pro regresní koeficienty:
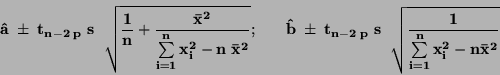 |
(79) |
Interval spolehlivosti pro vyrovnávanou hodnotu:
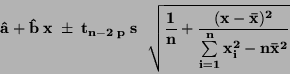 |
(80) |
© František Šťastný, 1997
![]() , zadané hodnotami
, zadané hodnotami
![]() vhodnou aproximující funkcí
vhodnou aproximující funkcí ![]() .
Za aproximující funkci
.
Za aproximující funkci ![]() se často volí lineární kombinace
elementárních funkcí
se často volí lineární kombinace
elementárních funkcí ![]() .
.
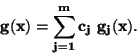
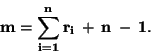
![]() , kdy se konstruuje polynom stupně
nejvýše
, kdy se konstruuje polynom stupně
nejvýše ![]() , interpolující
, interpolující ![]() uzlových bodů, a kdy platí
uzlových bodů, a kdy platí
![]() . Interpolační polynom splňující tyto podmínky lze
vyjádřit jako lineární kombinaci všech y-ových hodnot
. Interpolační polynom splňující tyto podmínky lze
vyjádřit jako lineární kombinaci všech y-ových hodnot
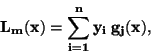
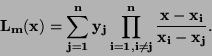
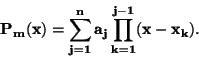
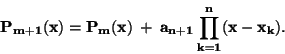
![]() se svou první
derivací souhlasil ve všech uzlových bodech s danou funkcí a její první
derivací. To znamená, že
se svou první
derivací souhlasil ve všech uzlových bodech s danou funkcí a její první
derivací. To znamená, že
![]() a interpolační polynom
je stupně
a interpolační polynom
je stupně ![]() . Podrobnosti naleznete opět v
. Podrobnosti naleznete opět v ![]() .
.
![]() definována jako podíl
polynomu stupně
definována jako podíl
polynomu stupně ![]() (v čitateli) a polynomu stupně
(v čitateli) a polynomu stupně ![]() (ve jmenovateli).
(ve jmenovateli).
![\includegraphics[height=10cm, width=\textwidth, keepaspectratio=false]{inter}](img369.png)
![]() nezávisle proměnné
získáme měřením odpovídající hodnoty závisle proměnné
nezávisle proměnné
získáme měřením odpovídající hodnoty závisle proměnné
![]() .
Tyto hodnoty nesplňují regresní model přesně, ale jsou zatíženy chybami.
Například pro lineární regresy je možno psát:
.
Tyto hodnoty nesplňují regresní model přesně, ale jsou zatíženy chybami.
Například pro lineární regresy je možno psát:
![]() ,
kde
,
kde ![]() jsou chyby.
jsou chyby.
![]()
![]() a odhad rozptylu
a odhad rozptylu ![]() :
:
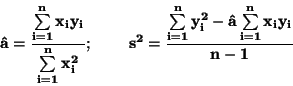
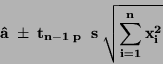
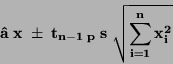
![]()
![]() a odhad rozptylu
a odhad rozptylu ![]() :
:
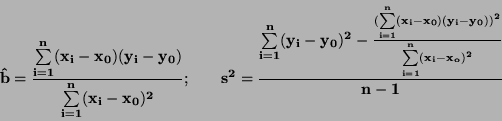

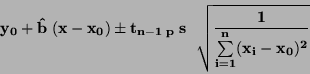
![]()