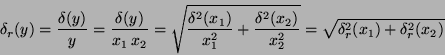Subsections
Při vlastním měření přestavuje měřená veličina 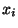 zřídka požadovaný
výsledek měření. Většinou je nutno naměřit
veličiny
zřídka požadovaný
výsledek měření. Většinou je nutno naměřit
veličiny
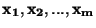 a výslednou veličinu
a výslednou veličinu 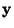 vypočítat ze vztahu
vypočítat ze vztahu
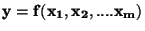 .
K odhadu střední hodnoty hledané veličiny a rozptylu lze použít:
.
K odhadu střední hodnoty hledané veličiny a rozptylu lze použít:
- metody Taylorova rozvoje funkce
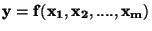
- metody dvoubodové aproximace
- metody simulačního výpočtu Monte Carlo
Při běžných měřeních ve fyzice se nejvíce používá metoda Taylorova rozvoje.
Metoda dvoubodové aproximace je založena na náhradě rozdělení pravděpodobnosti
funkce
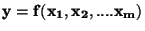 dvoubodovým rozdělením se stejnou střední
hodnotou a rozptylem
dvoubodovým rozdělením se stejnou střední
hodnotou a rozptylem ![$[6]$](img178.png) .
.
![\begin{displaymath}\bf
\hat{y} = \sum \limits_{i=1}^{m}\frac{f(\hat{x}_i + \ha...
... + \hat{s}_{x_i})
- f(\hat{x}_i - \hat{s}_{x_i})]^2}{4 \: m}
\end{displaymath}](img211.png) |
(33) |
Metoda Monte Carlo je počítačově orientovaná metoda vycházející z techniky
simulace experimentů metodou Monte Carlo ![$[6]$](img178.png) .
.
Podle Taylorovy věty ![$[1]$](img212.png) platí
platí
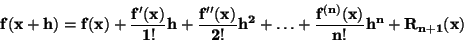 |
(34) |
Například:
Obdobně lze rozvést v řadu v okolí nějaké hodnoty i funkce více proměnných
Například v ![$[3]$](img216.png) najdeme následující jednoduché odvození zákona přenosu
chyb.
Mějme aritmetické průměry
najdeme následující jednoduché odvození zákona přenosu
chyb.
Mějme aritmetické průměry
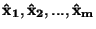
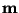 přímo měřených veličin
přímo měřených veličin
Odhad střední hodnoty hledané veličiny y vypočteme ze vztahu
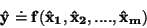 |
(35) |
Změnu y vyjádříme diferenciálem
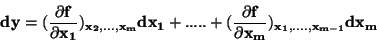 |
(36) |
Předpokládáme i platnost pro konečné odchylky
Předpokládejme, že každá z veličin 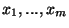 byla změřena n-krát.
Umocněním poslední rovnice a sečtením přes všechna
byla změřena n-krát.
Umocněním poslední rovnice a sečtením přes všechna 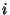 dostaneme
dostaneme
Po odmocnění dostaneme zákon přenosu (hromadění) chyb
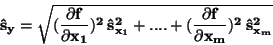 |
(37) |
Výše popsaný způsob odvození vyhovuje pro většinu případů určování
chyb měření ve fyzice, kdy se dá předpokládat, že měřené veličiny jsou na
sobě nezávislé, směrodatná odchylka je malá ve srovnání se střední hodnotou.
Přesnější odvození nalezneme například v ![$[6]$](img178.png) .
Postupuje se zde tak, že funkce
.
Postupuje se zde tak, že funkce
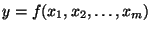 se v okolí
střední hodnoty
se v okolí
střední hodnoty
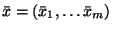 se rozvine v Taylorovu
řadu a vypočteme střední hodnotu a rozptyl. Složitost výpočtu záleží na počtu
členů řady, které musíme vzít v úvahu pro dosažení požadované přesnosti
výpočtu. Pro většinu běžných případ vystačíme pro rozptyl se vztahem
se rozvine v Taylorovu
řadu a vypočteme střední hodnotu a rozptyl. Složitost výpočtu záleží na počtu
členů řady, které musíme vzít v úvahu pro dosažení požadované přesnosti
výpočtu. Pro většinu běžných případ vystačíme pro rozptyl se vztahem
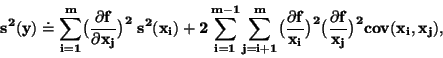 |
(38) |
kde
 kovariance mezi veličinami
kovariance mezi veličinami 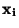 a
a 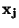 ,
která udává závislost mezi náhodnými veličinami
,
která udává závislost mezi náhodnými veličinami 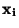 a
a 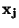 .
Platí
.
Platí
![$cov(x_i,x_j) = E[(x_i-\bar{x}_i)\; (x_j - \bar{x}_j)]$](img232.png) .
Pro případ vzájemně nezávislých veličin jsou kovariance rovny nule a dostaneme
výše odvozený zákon šíření chyb. S případů, kdy není možno kovarianci
veličin je možné připomenou například prokládaní přímky, popřípadě polynomu
experimentálními body metodou nejmenších čtverců. Počítáme-li chybu
bodů
.
Pro případ vzájemně nezávislých veličin jsou kovariance rovny nule a dostaneme
výše odvozený zákon šíření chyb. S případů, kdy není možno kovarianci
veličin je možné připomenou například prokládaní přímky, popřípadě polynomu
experimentálními body metodou nejmenších čtverců. Počítáme-li chybu
bodů
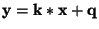 , je nutné uvažovat korelaci veličin
, je nutné uvažovat korelaci veličin 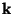 a
a 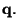
Použijeme následující značení:
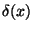 - chyba vyjádřená absolutně
- chyba vyjádřená absolutně
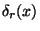 - chyba vyjádřená relativně (
- chyba vyjádřená relativně (
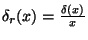 ).
Ze zákona přenosu chyb snadno odvodíme následující vztahy:
).
Ze zákona přenosu chyb snadno odvodíme následující vztahy:
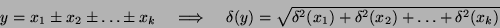 |
(39) |
 |
(40) |
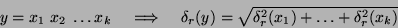 |
(41) |
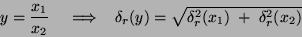 |
(42) |
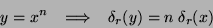 |
(43) |
Příklad: 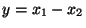 . Na základě zákona přenosu chyb odvoďte vztah pro
určení chyby
. Na základě zákona přenosu chyb odvoďte vztah pro
určení chyby 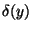 , znáte-li chyby
, znáte-li chyby 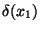 a
a 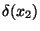 .
.
Příklad:
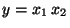 . Na základě zákona přenosu chyb odvoďte vztah
pro určení relativní chyby
. Na základě zákona přenosu chyb odvoďte vztah
pro určení relativní chyby 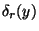 , znáte-li relativní chyby
, znáte-li relativní chyby
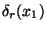 a
a
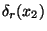 .
.
Příklad: Pro měření teploty v elektrickém kalorimetru používáme teploměr,
který měří teplotu 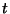 s chybou
s chybou
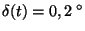 C. O kolik musí vzrůst
teplot v kalorimetru, abychom změnu teploty dokázali změřit
s relativní chybou 1%?
C. O kolik musí vzrůst
teplot v kalorimetru, abychom změnu teploty dokázali změřit
s relativní chybou 1%?
Označme
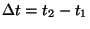 . Chyba
. Chyba
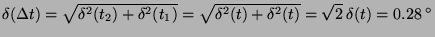 C.
C.
Relativní chyba
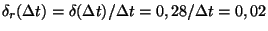 . Z této rovnice vyplývá, že
. Z této rovnice vyplývá, že
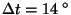 C.
C.
Příklad: Měření vlhkosti vzduchu ![$[2]$](img260.png) : Vzduch se nasává přes U trubici
s hygroskopickou látkou. Vážením trubice na analytických vahách dostaneme
hmotnost trubice před měřením
: Vzduch se nasává přes U trubici
s hygroskopickou látkou. Vážením trubice na analytických vahách dostaneme
hmotnost trubice před měřením 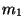 a hmotnost trubice po měření
a hmotnost trubice po měření 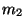 .
Objem nasátého vzduchu
.
Objem nasátého vzduchu 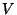 určíme z množství prokapané vody (hmotnosti
určíme z množství prokapané vody (hmotnosti 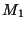 a
a 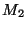 ).
).
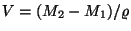 .
.
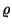 je měrná hmotnost vody.
je měrná hmotnost vody.
Pro vážení na analytických vahách obvykle platí:
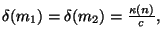 kde
kde 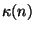 je krajní chyba čtení na stupnici vah, c je citlivost vah.
je krajní chyba čtení na stupnici vah, c je citlivost vah.
© František Šťastný, 1997
![]() zřídka požadovaný
výsledek měření. Většinou je nutno naměřit
veličiny
zřídka požadovaný
výsledek měření. Většinou je nutno naměřit
veličiny
![]() a výslednou veličinu
a výslednou veličinu ![]() vypočítat ze vztahu
vypočítat ze vztahu
![]() .
K odhadu střední hodnoty hledané veličiny a rozptylu lze použít:
.
K odhadu střední hodnoty hledané veličiny a rozptylu lze použít:
![\begin{displaymath}\bf
\hat{y} = \sum \limits_{i=1}^{m}\frac{f(\hat{x}_i + \ha...
... + \hat{s}_{x_i})
- f(\hat{x}_i - \hat{s}_{x_i})]^2}{4 \: m}
\end{displaymath}](img211.png)
![]() platí
platí
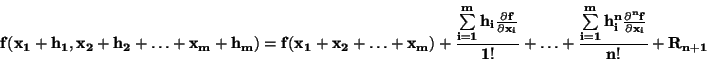
![]() najdeme následující jednoduché odvození zákona přenosu
chyb.
Mějme aritmetické průměry
najdeme následující jednoduché odvození zákona přenosu
chyb.
Mějme aritmetické průměry
![]()
![]() přímo měřených veličin
přímo měřených veličin
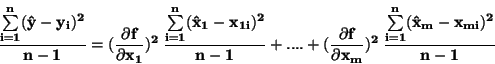
![]() .
Postupuje se zde tak, že funkce
.
Postupuje se zde tak, že funkce
![]() se v okolí
střední hodnoty
se v okolí
střední hodnoty
![]() se rozvine v Taylorovu
řadu a vypočteme střední hodnotu a rozptyl. Složitost výpočtu záleží na počtu
členů řady, které musíme vzít v úvahu pro dosažení požadované přesnosti
výpočtu. Pro většinu běžných případ vystačíme pro rozptyl se vztahem
se rozvine v Taylorovu
řadu a vypočteme střední hodnotu a rozptyl. Složitost výpočtu záleží na počtu
členů řady, které musíme vzít v úvahu pro dosažení požadované přesnosti
výpočtu. Pro většinu běžných případ vystačíme pro rozptyl se vztahem
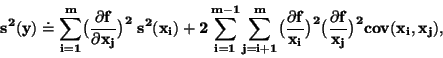
![]() - chyba vyjádřená absolutně
- chyba vyjádřená absolutně
![]() - chyba vyjádřená relativně (
- chyba vyjádřená relativně (
![]() ).
Ze zákona přenosu chyb snadno odvodíme následující vztahy:
).
Ze zákona přenosu chyb snadno odvodíme následující vztahy: