7. Slitiny.
Fyzikální vlastnosti pevných látek (ale i kapalin a plynů) často značně závisí na přítomnosti cizích atomů, příměsí a nečistot. V případě pevných látek pak mluvíme o slitinách. Protože slitiny mívají v mnoha případech lepší vlastnosti než čisté látky, má jejich studium velký praktický význam.
7.1. Fáze a fázové přeměny.
Podle J.W.Gibbse zní definice fáze následovně: Jestliže soustava je v celém svém objemu jednolitá a to nejen po stránce chemického složení, ale i po stránce fyzikálního stavu, říkáme o ní, že je homogenní, nebo že se skládá z jediné fáze.
Pojem fáze může být názorně objasněn pomocí Obr.7.1.

Obr. 7.1. K objasnění pojmu fáze.
Matematicky lze situaci na tomto obrázku charakterizovat tzv. Gibbsovým pravidlem fází:
F = C – P + 2 (7.1)
kde C je počet složek v soustavě, P je počet fází a F je počet stupňů volnosti (teplota, tlak, složení), které lze nezávisle měnit, aniž dojde ke změně rovnováhy fází. Jako příklad, na němž toto pravidlo objasníme, uvádíme fázový diagram čistého Mg (jednosložkový fázový diagram) – Obr.7.2.

Obr.7.2. Fázový diagram hořčíku.
Předpokládejme nejdříve, že se soustava nachází při tlaku a teplotě, které odpovídají bodu A. Potom C = 1 (čistý Mg), P = 1 (kapalina), takže F = 1 – 1 + 2 = 2. Vychází nám tedy dva stupně volnosti a můžeme měnit buď teplotu, nebo tlak, nebo obojí a stále se budeme nacházet v „kapalné“ oblasti diagramu. Podobně máme pro bod B: C = 1, P = 2 (pevná a kapalná fáze) a tedy F = 1 (měníme-li např. tlak, bude se měnit zároveň i teplota – nacházíme se na křivce CB). Nakonec pro bod C máme C = 1, P = 3 a tedy F = 0 (trojný bod, daný pevnými hodnotami tlaku a teploty.
Podobně jako je tomu u kapalin (Obr.7.1), existují i u pevných látek tři případy rozpustnosti jedné látky ve druhé: úplná rozpustnost, částečná rozpustnost a nerozpustnost. Na Obr.7.3a,b. je znázorněn případ úplné a částečné rozpustnosti (Ni v Cu a Zn v Cu). Z tohoto obrázku vidíme, že v případě částečné rozpustnosti Zn v Cu vzniká jak tuhý roztok, tak i sloučenina CuZn (Obr.7.3c). Fázový diagram pro tuto slitinu je na Obr.7.4. Podmínky pro rozpustnost atomů A v atomech B jsme si uvedli v odstavci 4.1.2.
Rozpustnost v pevném stavu není omezena jenom na kovy. Na Obr. 7.5. je ukázán příklad úplné rozpustnosti v případě keramických materiálů MgO a NiO. Jedná se o úplnou rozpustnost proto, že obě sloučeniny mají stejnou krystalovou strukturu a blízké poloměry iontů i stejné mocenství.

Obr.7.3. Úplná rozpustnost atomů Ni v Cu a částečná rozpustnost atomů Zn v Cu.

Obr.7.4. Fázový diagram slitiny CuZn

Obr.7.5. Příklad úplné rozpustnosti v případě keramických materiálů.
7.2. Binární slitiny v případě úplné rozpustnosti.
V případě úplné rozpustnosti jedné látky v druhé má fázový diagram v proměnných teplota – složení tvar, uvedený pro slitiny CuNi (Obr.7.6.). Jako liquidus je zde označena čára, rozdělující oblast kapalné fáze a oblast, v níž dochází ke krystalizaci pevné fáze (stále ve fázi kapalné). Solidus je název pro křivku, oddělující tuto posledně jmenovanou oblast od pevné fáze slitiny. Z Obr.7.6 plyne, že slitina Cu+40wt%Ni tuhne v oblasti teplot 1280 0C – 1240 0C. Písmenem a je označen tuhý roztok CuNi. Podobný fázový diagram má i slitina (Ni,Mg)O (Obr.7.7.).

Obr.7.6. Binární slitina CuNi.
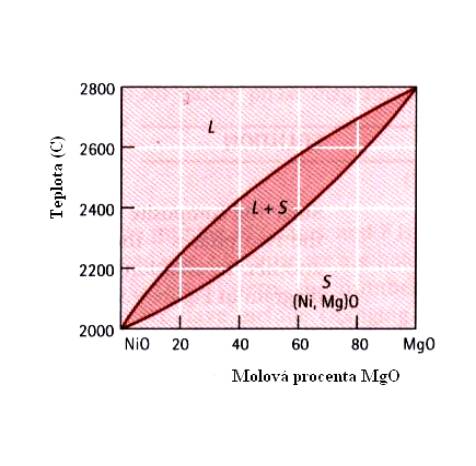
Obr.7.7. Fázový diagram slitiny (Ni,Mg)O – viz Obr.7.5.
Jako příklad pro lepší pochopení použití fázového diagramu popíšeme složení slitiny Cu+40wt%Ni (známou z Obr.7.6) při teplotách 1300 0C, 1270 0C, 1250 0C a 1200 0C. Z Obr. 7.8 a 7.9. plyne, že při teplotě 1300 0C je slitina v tekutém stavu (tvoří jednu fázi – taveninu). Při teplotě 1270 0C, nacházející se v oblasti mezi liquidem a solidem dostáváme dvě fáze, tuhý roztok a-CuNi a kapalnou fázi této slitiny. Abychom popsali poměry v této oblasti, vedeme rovnoběžku s osou x (složení slitiny). Ta protne liquidus v bodě, odpovídajícím 37%Ni a solidus v bodě pro 50%Ni. Lze tedy říci, že pro teplotu 1270 0C se v roztoku slitiny CuNi začínají tvořit zmíněné krystalky a CuNi, přičemž kapalná fáze se ochudí o Ni (bude ho obsahovat jenom 37%) a naopak pevná fáze ho bude obsahovat více (50%). Při teplotě 1250 0C budou existovat opět dvě fáze, kapalná bude ještě chudší na Ni (pouze 32%) a pevná ho bude obsahovat 45%. Při teplotě 1200 0C dojde k úplnému ztuhnutí slitiny, která bude nyní obsahovat 40%Ni a 60%Cu.

Obr.7.8. K objasnění možností fázového diagramu.

Obr.7.9. Detail z Obr.7.8.
Názorně je struktura, vznikají při tuhnutí slitiny CuNi, zobrazena na Obr.7.10. pro případ rovnovážného (pomalého) tuhnutí, kdy je umožněna dostatečná difúze atomů Cu a Ni, takže vznikne homogenní rovnovážná struktura slitiny. Pokud je tuhnutí nerovnovážné, je situace složitější a její výklad vychází za rámec této kapitoly.

Obr.7.10. Struktury, vznikající při tuhnutí slitiny CuNi.
7.3. Binární slitiny v případě částečné rozpustnosti.
V případě částečné rozpustnosti má fázový diagram mnohem složitější tvar, který si názorně ukážeme na Obr.7.11. pro případ slitiny PbSn. Na Obr. 7.12. je podrobněji ukázán vznik struktury slitiny pro případ malých koncentrací Sn v Pb. Na dalším obrázku (Obr.7.13) je situace poněkud složitější (slitina Pb+10wt%Sn) – vznikají precipitáty (tzv. b - fáze), rozptýlené ve fázi a (tuhý roztok).
Zvláštním případem je tzv. eutektická slitina takového složení, že z kapalné fáze tuhne přímo pevná fáze, aniž tuhnutí prochází oblastmi, v nichž je tuhnoucí fáze obklopena fází kapalnou. (Obr.7.14). Složení eutektické slitiny ( v tomto případě Pb+61,9wt%Sn) má výraznou lamelární strukturu.

Obr.7.11. Fázový diagram slitiny PbSn (částečná rozpustnost).

Obr.7.12. Struktura slitiny PbSn pro malé koncentrace Sn v Pb.

Obr.7.13. Struktura slitiny PbSn pro vyšší koncentrace Sn v Pb (kolem 10 wt% Sn)

Obr.7.14. Struktura eutektické slitiny PbSn.

Obr.7.15. Fázový diagram technicky významných ocelí.
Ještě složitější situace nastává v případě, kdy je rozpustnost jednoho prvku velmi malá, jako je tomu v případě oceli (Fe + C). Fázový diagram pro technicky významné oceli je uveden na Obr.7.15. (pro vyšší koncentrace uhlíku dostáváme technicky nevyužívané slitiny, připomínající keramika či strusku). Z tohoto obrázku vidíme, že v případě ocelí je situace ještě mnohem složitější, než pro dosud probírané binární slitiny a ocelím budeme věnovat zvláštní kapitolu.
8. Tření.
Ze zkušenosti víme, že vyrobit ideálně hladký povrch
pevné látky bude asi dosti obtížné, ne-li nemožné. I tzv. zrcadlově hladký
povrch kovu se nám při dostatečném zvětšení jeví jako hrbolatý (Obr. 8.1).
Proto posouváme-li po sobě dvě tělesa, budou mezi nimi působit tzv. síly tření. Tyto síly dělíme na síly tření smykového, valivého, řemenového a
vrtného. Z jiného hlediska dělíme tření na tření suché a mokré.

Obr.8.1. 1500 x
zvětšený povrch vyleštěné ložiskové oceli.
8.1. Tření smykové (suché).
Tření smykové vzniká při pohybu jednoho tělesa po
druhém (předpokládáme, že obě plochy jsou rovinné). Pro sílu tření mezi oběma
tělesy platí experimentálně určený Coulombův – Amontův zákon:
Ft
= m.N (8.1)
kde
m je koeficient
tření a N je kolmý tlak, tj. složka
výsledné síly, kolmá k třecí ploše.
Koeficient tření je funkcí (zřejmě kromě jiných
parametrů) rychlosti vzájemného pohybu obou těles (Obr.8.2 ). Jeho závislost na
době, po kterou obě tělesa na sobě spočívají, je uvedena na Obr.8.3. Na
Obr.8.4.je vynesena závislost síly tření na
čase. Z obrázku plyne z praxe známá zkušenost: táhneme – li např. sáně po umrzlém sněhu,
musíme nejdříve působit dosti velkou silou, než se dají do pohybu. Po překonání
jisté maximální síly při níž se sáně daly do pohybu je síla, potřebná
k jejich dalšímu pohybu již menší.
Obě tyto závislosti lze kvalitativně vysvětlit pomocí
tzv. teorie mikrosvárů. Základní
myšlenka této teorie plyne z Obr.8.5., kde jsou schematicky znázorněny dva
po sobě klouzající povrchy (právě v místech, kde se vzájemně dotýkají
„výstupky“ obou ploch, dochází k tak těsnému kontaktu, že atomy obou
povrchů jsou ve vzájemném kontaktu, a budou na sebe působit meziatomovými
silami – vzniknou mikrosváry)..
V případě kovů je situace komplikována v důsledku heterogenní vrstvy,
která vzniká na jejich povrchu v důsledku oxidace a technologického
zpracování (Obr.8.6. ).


Obr.8.2.
Závislost koeficientu tření
Obr.8.3. Závislost koeficientu tření
na rychlosti pohybu. na čase (do začátku pohybu)

Obr.8.4. Závislost síly tření (koeficientu tření) na tažné síle (čase).

Obr.8.5.
Vzájemný vztah mezi skutečnou a zdánlivou třecí plochou.

Obr.8.6.
Schematické znázornění složité situace na povrchu kovů.
V Tabulce 8.1. jsou uvedeny koeficienty tření pro
některé v praxi používané dvojice materiálů
Tab.8.1.
|
Materiál |
m |
Materiál |
m |
|
Dřevo – dřevo (suché) |
0,40 |
Kov – kov (olej) |
0,05 |
|
Dřevo – dřevo (namydlené) |
0,20 |
Velmi dobře vyleštěné plochy |
0,03 |
|
Kov – dubové dřevo (suché) |
0,55 |
Ocel – achát (suché) |
0,20 |
|
Kov – dubové dřevo (mokré) |
0,25 |
Ocel – achát (olej) |
0,11 |
|
Kůže - dub |
0,32 |
Ocel – křemen (suché) |
0,50 |
|
Kůže – kov (suché) |
0,56 |
Pneumatika –beton (suché) |
0,70 |
|
Kůže – kov (mokré) |
0,36 |
Pneumatika – beton (mokré) |
0,25 |
|
Kůže – kov (olej) |
0,15 |
Dřevo - kámen |
0,40 |
|
Kov – kov (suché) |
0,17 |
Teflon - teflon |
0,07 |
|
Kov – kov (mokré) |
0,30 |
Nylon - nylon |
0,25 |
8.2. Měření koeficientu tření.
Koeficient tření m lze měřit různými metodami. Některé z nich jsou
uvedeny na Obr. 7,8 a 9 a jejich princip je patrný z obrázků.
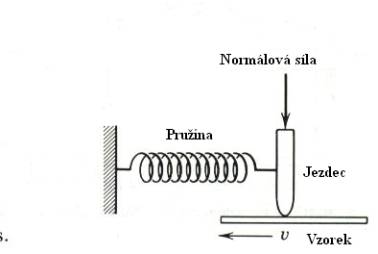
Obr.7. Měření koeficientu tření

Obr.8. Měření koeficientu tření

Obr.9. Měření koeficientu tření
Základní zákony suchého tření lze shrnout do několika bodů:
a)
Úměra mezi velikostí
třecí síly a kolmým tlakem je důsledkem skutečnosti, že každá z obou
veličin závisí na materiálových konstantách, charakterizujících obě kontaktní
plochy, násobené toutéž hodnotou skutečné kontaktní plochy AS.
b)
Nezávislost třecí síly
na zdánlivé kontaktní ploše AZ lze objasnit pomocí představy, že to je skutečná a
nikoliv zdánlivá plocha, která řídí interakci mezi oběma tělesy. A tato
skutečná plocha nezávisí na ploše zdánlivé.
c)
Poměrně slabá závislost
třecí síly na rychlosti pohybu obou těles po sobě (Obr.8.2.) souvisí
s malou závislostí mezi napětím a deformací v plastické oblasti
většiny materiálů. Tam, kde je tato závislost výraznější, je výraznější i
závislost třecí síly na rychlosti pohybu.
d)
Slabá závislost třecí
síly na drsnosti třecích ploch (Obr.8.10.) souvisí s tím, že nejvíce
deformační práce se spotřebuje na vyvolání smykového posunutí výstupků na
plochách (na rozdíl od mnohem menší práce, spotřebované na jejich vzájemné
„obcházení“, tj. klouzání po sobě)

Obr.8.10. Závislost koeficientu tření na drsnosti povrchu.
8.3. Snížení
tření mazáním.
Praxe nám ukazuje, že suché tření lze
značně snížit, použijeme – li maziv. Způsoby mazání můžeme rozdělit do tří skupin:
a)
Mazání pomocí tenkého
kapalného filmu. V ideálním
případě takového mazání jsou obě třecí plochy vzájemně odděleny tenkou vrstvičkou
vhodné kapaliny. Mezera mezi oběma plochami bývá velká ve srovnání
s jejich drsností. Koeficient tření je v tomto případě dán
vlastnostmi mazací kapaliny, zejména její viskozitou. Proto hovoříme o tzv. hydrodynamickém mazání. (Obr.8.11. )
b)
Mazání pomocí
vytvoření povrchové vrstvičky. Tento
způsob mazání spočívá ve vytvoření dvou povrchových vrstviček na obou třecích
plochách tak, aby nedošlo ke vzájemnému kontaktu kovů. Zmíněné vrstvičky jsou
vytvořeny pomocí adsorpce různých maziv (minerální či rostlinné oleje, tuky,
mastné kyseliny, mýdla apod.). Tento způsob mazání se používá většinou při
nižších teplotách a tlacích. Pro vysoké teploty a tlaky se tyto vrstvičky
vytvářejí pomocí různých aditiv,
přidávaných do minerálních olejů (fosfor, chlór a síra). Tak vzniknou poměrně
pevné vrstvičky (soli), které mají vysokou teplotu tání a brání přímému
kontaktu obou kovů mezi sebou.
c)
Mazání pomocí tuhých
maziv. Mezi tuhá maziva řadíme
grafit, sirník molybdenu a teflon. Tyto látky aplikujeme ve formě prášku, který
přilne k oběma třecím plochám a chemicky s nimi reaguje. Posláním
těchto maziv je oddělit od sebe obě třecí plochy prostředím s malým
koeficientem tření. Tohoto způsobu mazání se používá při vysokých teplotách a
tlacích a v agresivním prostředí, kde jsou jiné druhy maziv neefektivní.

Obr.8.11. Základní principy mazání: a) hydrodynamické, b)
pomocí adsorbovaných
tenkých vrstviček,
c) pomocí tuhých maziv, d) suché tření.
Konkrétní druhy maziv a jejich
vlastnosti :
-
Minerální oleje: Vyrábějí se z ropy a vytvářejí na povrchu
třecích ploch tenké povrchové vrstvičky. Jsou velmi rozšířené.
-
Rostlinné oleje, tuky
a jejich deriváty: Vyrábějí se z rostlin a zvířecích tuků.
Patří k prvním používaným mazivům. Řadíme k nim i mýdla, tuky, vosky
a mastné kyseliny.
-
Syntetická kapalná
maziva: Většinou jsou svojí
strukturou podobné olejům. Patří sem syntetické estery a silikonové oleje.
Používají se za vysokých teplot.
-
Kompozitní maziva: Sem řadíme
minerální oleje, doplněné tzv. aditivy, kterými jsou: (1) sloučeniny fosforu,
síry a chlóru. (2) Pevné látky, jako grafit a sirník molybdenu. (3) Oxidační
inhibitory. (4) Přídavky, zamezující pěnění. (5) Přídavky proti množení
bakterií a jiných organismů.
-
Vodní maziva: Voda je sama o sobě špatné mazivo, avšak přidáme – li
do ní vhodné látky, můžeme ji k mazání použít, neboť má dobré chladící
schopnosti. Jako přísady můžeme použít olej (emulze s vodou), nebo i jiné
speciální chemikálie, rozpustné ve vodě.
-
Povrchové vrstvy: Povrchy třecích ploch lze pokrýt například (1) kovy
(Zn, Sn apod.), které na nich vytvářejí plastické povlaky. (2) polymery
(teflon). (3) skla (pro vysoké teploty.
Obecně lze říci, že nejlepší maziva mají takovou
strukturu, že jejich molekuly jsou tvořeny dlouhými řetězci, ukončenými
nenasycenou vazbou (která se naváže na jednu z ploch). Mazací účinek potom
připomíná „klouzán퓨po mokré trávě. (Obr.8.12)


a) b)
Obr.8.12. Princip mazání: a) nepříliš efektivní maziva, b)
velmi dobrá maziva.
8.4. Mokré (vazké) tření.
Z předcházejícího odstavce plyne, že použití
kapalin jako maziv značně snižuje tření obou
třecích ploch. Názorně si to lze představit tak, že se po sobě již
nepohybují obě plochy, ale tenké vrstvičky kapaliny (maziva) – tzv. mokré tření. Podobně je tomu
v případě, že se v nějaké kapalině pohybuje těleso (např. kulička o
poloměru r). V obou případech
pozorujeme, že statické tření je nulové (obě třecí plochy se po sobě začnou
pohybovat už při působení nepatrné síly). Je to rozdíl proti suchému tření, u
kterého bylo třeba působit jistou (někdy dosti značnou silou), aby se tažené
těleso dalo do pohybu (viz Obr. 8.4.).
Závislost síly mokrého tření na rychlosti je
schematicky znázorněna na Obr. 8.13 .

Obr. 8.13. Schematická závislost síly mokrého tření na
rychlosti.
Matematicky
lze tuto závislost popsat Stokesovým vztahem
Ft = 6.p.h.r.v = b.v (8.2)
Kde
h je vazkost
kapaliny a r je charakteristický rozměr
těles (poloměr kuličky, vzdálenost třecích ploch, apod.). Z Obr.8.13.
plyne, že pro větší rychlosti se přímá úměrnost změní na kvadratickou závislost
(Newtonův vztah):
Ft = C.v2 (8.3)
8.4. Valivé tření.
V předcházejících odstavcích jsme si ukázali, že
suché tření lze snížit např. výběrem vhodných materiálů pro třecí plochy, nebo
mazáním. Další cestou je použití valivých ložisek, tj. přeměnou suchého nebo
mokrého tření na tření valivé.
Při valivém pohybu pevného oblého tělesa (kuličky,
válečku) po jiném pevném tělese, k němuž je oblé těleso přitlačováno
nějakou silou (a navíc tlačeno ve směru, rovnoběžném s rovinou druhého
tělesa), odporuje tomuto pohybu tzv.
tření valivé. Fyzikální podstatu valivého tření lze objasnit pomocí
Obr.8.14. a 8.15. Protože na kuličku (váleček) působí síla, která ji vtlačuje
do podložky (a zároveň ji pohání jedním směrem, což je typické pro praktické
využití jako kuličková nebo válečková ložiska), dojde k deformaci jak
kuličky, tak i podložky. Pokud by tato deformace byla ideálně pružná,
nevznikala by síla valivého tření. Celková síla, působící na kuličku, je podle
tohoto obrázku rovna F = F1 + F2 a momenty těchto sil vzhledem k ose kuličky se
navzájem vyruší. Výslednice F je v rovnováze s vnější silou, působící na
kuličku (zvětšenou o její tíhu). Nevzniká tedy žádná síla valivého tření.


Obr.8.14. K objasnění valivého tření. Obr.8.15. Síly
při valivém tření.
Protože je tato deformace plastická (i když velmi
malá), vzniká síla valivého tření a síly F1 a F2 budou různé, takže jejich výslednice bude mít složku
vertikální i horizontální. Momenty obou sil mají opačný směr a nerovnají se
jeden druhému. Moment síly F2, brzdící otáčení kuličky je větší, než moment síly F1, který ji urychluje, takže výsledkem je zpomalování rotace kuličky a
tedy vznik valivého tření.
Síla valivého tření je tedy důsledkem nepružného
charakteru deformace kuličky (válečku) a povrchu ložiska v okolí jejich
vzájemného kontaktu. Vztah pro sílu valivého tření má tvar
 (8.4)
(8.4)
( mv je
koeficient valivého tření, r je poloměr
kuličky a N je kolmý tlak, který na ni
působí)..Hodnota koeficientu valivého tření mv (v cm) je
vždy menší, než je koeficient suchého tření, například (viz Tab.8.2):
|
Dvojice materiálů |
mv (cm) |
|
Tvrdé dřevo – tvrdé dřevo |
0,05 |
|
Ocel - ocel |
0,005 |
|
Ocelové kuličky v ložiskách |
0,0005 – 0,001 |
Odtud
vidíme, jak je vhodné převádět suché i mokré tření na tření valivé; (je –li to
možné).
Zákony
valivého tření lze opět shrnout do několika bodů:
a)
Síla valivého tření je
rovna mocnině zatěžovací síly. Pro malá zatížení, kdy jke deformace kuličky i
podložky prakticky pouze pružná, je exponent mocniny ~ 1,3.
Pro velká zatížení, kdy již plastická deformace na styku kuličky a plochy není
zanedbatelná je exponent větší, dosahuje až hodnot 2,0.
b)
Síla valivého tření je
nepřímo úměrná poloměru křivosti kuličky (válečku).
c)
Síla valivého tření je
tím menší, čím hladší jsou oba povrchy (kuličky i povrchu ložiska).
9. Povrchové napětí kapalin. Povrchová energie
pevných
látek. Tekuté
krystaly.
9.1. Povrchové napětí kapalin.
Kapalné skupenství látek je s jedné strany ohraničeno skupenstvím pevným a s druhé strany skupenstvím plynným. Proto je přirozené očekávat, že kapaliny budou mít vlastnosti a strukturu, nacházející se někde mezi uspořádanými pevnými látkami a chaotickými plyny. Hustota kapalin se příliš neliší od hustoty pevných látek (kde se atomy nacházejí v těsné blízkosti) a proto i v kapalinách budou tyto částice (atomy nebo molekuly) dosti blízko u sebe, ale přitom nebudou na sebe vázány tak velkými silami jako v pevných látkách (proto kapaliny nemají stálý tvar), ale přesto ještě dosti velkými (takže kapaliny udržují svůj objem)..
Podle Frenkela připomíná pohyb částic v kapalinách pohyb kočovníků: částice poskočí o malý úsek, chvíli kmitá na místě a opět poskočí náhodným směrem a zase kmitá, atd.
Vyjdeme-li tedy z tohoto kvalitativního modelu kapaliny a vybereme-li si jednu částici uvnitř kapaliny, můžeme říci, že výslednice meziatomových (nebo mezimolekulárních) sil, které na ni působí, je nulová. Zcela jinak je tomu blízko povrchu a na povrchu kapaliny. Tam je výslednice sil, působících na částici nenulová a směřuje dovnitř kapaliny (Obr.9.1). Situace je tedy taková, jakoby byla kapalina stlačena silou, působící směrem dovnitř kapaliny. Ta síla je, ač se to na první pohled nezdá, značná – kapalina je stlačena tak, že se jeví navenek jako téměř nestlačitelná. Jinými slovy to znamená, že na povrchu kapaliny je něco, co připomíná tenkou elastickou blanku, snažící se co nejvíce zmenšit svůj povrch (Obr.9.2).


Obr.9.1. Ke vzniku síly povrchového Obr.9.2. Směr síly povrchového napětí .
Například v beztížném stavu zaujme pod vlivem této síly kapalina tvar koule (při daném objemu má minimální povrch). Stejně je tomu i v případě, že výslednice sil, působících na kapalinu, je nulová (Obr.9.3.)

Obr.9.3. Tvar povrchu kapaliny v beztížném stavu (po dopadu kapičky na
povrch kapaliny vznikne v jistém kratičkém časovém intervalu tento
tvar povrchu kapaliny. Síla tíhová je zde rovna síle setrvačné směrem
nahoru a dochází pro tuto chvíli k beztížnému stavu. Jedinou silou,
působící na kapičku, je síla povrchového napětí).
Povrchové napětí je definováno jako síla dF, působící na jednotku délky povrchu dl (tečně k povrchu kapaliny)
![]() (7.1)
(7.1)
Nebo jako energie dE jednotky povrchu kapaliny dS
![]() (7.2)
(7.2)
(v tomto případě se jedná o tzv. volnou energii, definovanou v termodynamice pomocí vztahu dE = -S.dT – p.dV, kde S je entropie soustavy, charakterizující její uspořádání a p, T a V jsou její tlak, teplota a objem. Dochází-li ke změně povrchu kapaliny izotermicky, je teplota konstantní a tedy dT = 0 a změnu objemu lze snadno převést na změnu povrchu)
Povrchové napětí kapalin závisí na více parametrech (to plyne z Obr.9.1.) Bude záviset na kvalitě přechodu kapalina – plyn i na prostředí nad kapalinou, tedy zřejmě na hustotě obou prostředí, teplotě, tlaku čistotě kapaliny, apod.:
s = f (T, p, r, čistota, tenze par, ….) (7.3)
Obdobu povrchového napětí kapalin mají i pevné látky (ztuhnutím by se nemělo nic příliš měnit na kvalitativním Obr.9.1). V případě pevných látek se povrchové napětí nazývá povrchovou energií pevných látek. Proto můžeme kvalitativně i kvantitativně objasnit tvar povrchu kapaliny na rozhraní tří prostředí, pevného, kapalného a plynného, stejně jako tvar kapiček jedné kapaliny na povrchu druhé (nejsou-li navzájem rozpustné), nebo na povrchu pevné látky. Některé z těchto případů jsou uvedeny na Obr.9.4 a 9.5.

Obr.9.4. Tvar kapiček jedné kapaliny na kapalině druhé.

Obr.9.5. Tvar kapiček kapaliny na pevném povrchu (např. skle).
9.2. Výskyt a využití povrchového napětí.
Jevy povrchového napětí pozorujeme téměř všude v přírodě kolem nás a nacházejí využití v mnoha odvětvích lidské činnosti, v chemii, biologii, v domácnosti, průmyslu, zemědělství, atd. Uvedeme přehled alespoň některých z nich:
a) Využití v chemii: jevy povrchového napětí jsou podstatou celých odvětví chemie, jako je např. koloidní chemie, chromatografie, vysvětluje vlastnosti povrchově aktivních látek a katalyzátorů, atd.
b) Využití v biologii: povrchové napětí vysvětluje mnoho jevů, souvisejících s činností buněk, stejně jako kapilární jevy v rostlinách, atd.
c) Využití v domácnosti: mytí, praní, holení, jsou činnosti, které mají společnou podstatu. Jde o umožnění smáčení nečistot a tím jejich odstranění. Studená voda má vysoké povrchové napětí a tak abychom ji mohli použít k výše uvedeným činnostem, musíme toto napětí snížit (ohřátím, přidáním látek, snižujících povrchové napětí – mýdla, saponátů apod.).
d) Využití v zemědělství: aby bylo možno správně aplikovat herbicidy a insekticidy, je třeba upravit vhodně povrchové napětí postřiků (aby buď ulpěly, nebo neulpěly na daném druhu rostliny – kulturní či plevelné)
e) Využití v průmyslu: technologický postup, zvaný flotace spočívá v oddělování hlušiny od těžené látky (železa, zlata apod.). Kapalina s vhodně upraveným povrchovým napětím (voda + saponát) způsobí, že hlušina bude smáčena a klesne ke dnu a nemáčená látka, na níž se vytvoří vzduchové bublinky vyplave na hladinu. Fyzikální podstata broušení je založena na skutečnosti, že vhodná kapalina sníží povrchové napětí broušených či obráběných látek. Chceme-li například vrtat otvor ve skle, lze to provést s úspěchem pod vodou (sklo se však musí pečlivě odmastit).
f) Přírodní jevy: existence povrchového napětí vysvětluje takové jevy, jako je pohyb drobného hmyzu po vodní hladině, „plavání“ drobných předmětů (žiletka, jehla, hliníková mince) na hladině vody (Obr.9.6.), jaká síla způsobí změnu tvaru špičky štetce po namočení, apod.(Obr.9.7.). Rovněž objasní důvod, proč voda nepronikne peřím vodních ptáků a ti mohou snadno plavat po vodní hladině (Obr. 9.8). a naopak důvod, proč se tito ptáci utopí, když je zasáhne ropná skvrna na hladině. I tvar kapek rosy na listech a květech rostlin souvisí s povrchovým napětím vody (Obr.9.9.). Velkou většinu meteorologických jevů lze také objasnit povrchovým napětím vody (elektrický náboj v bouřkových mracích, tvar vodních kapek, vznik krup, apod.).


Obr.9.6. Drobné kovové předměty Obr.9.7. Síla povrchového napětí
„plavou“ na povrchu kapaliny stáhne po namočení štetec
díky povrchovému napětí. do špičky.


Obr.9.8. Kapičky vody na ptačím peří. Obr.9.9. Kapičky vody na nesmáčivém
povrchu okvětních lístků růže.
9.3. Měření povrchového napětí.
Povrchové napětí lze měřit buď metodami přímými, nebo nepřímými:
a) Přímá metoda, vycházející z definice: tato metoda vychází ze vztahu (9.1) a Obr.9.10. . Do měřené kapaliny ponoříme tělísko definovaného tvaru o známé délce a měříme
sílu, potřebnou k vytažení tělíska z kapaliny.

Obr.9.10. Princip přímé metody měření povrchového napětí.

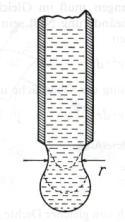
Obr.9.11. Metoda ze vzestupu v kapiláře. Obr.9.12. Kapková metoda.
b) Metoda, využívající vzestupu v kapiláře: z Obr.9.11. plyne, že síla povrchového napětí je v rovnováze tíhou sloupce kapaliny. Toho lze využít k měření povrchového napětí kapalin (je třeba změřit hustotu kapaliny a poloměr kapiláry.
c) Metoda kapková: necháme-li odkapávat kapalinu z tenké trubičky (Obr.9.12.), můžeme tvrdit, že kapička odkápne tehdy, když je síla tíhová rovna síle povrchového napětí, působící na obvodu kapiláry. Skutečnostně však taková, že kapička neodpadne celá a část jí zůstane na konci kapiláry. Proto tuto metodu užíváme jako metodu relativní, tj. srovnáváme tíhu určitého počtu kapek neznámé kapaliny se stejným počtem kapiček kapaliny se známým povrchovým napětím (a předpokládáme, že zbytek kapaliny, který neukápl, je stejný pro obě kapaliny).
9.4. Tekuté krystaly.
Na přelomu 19. a 20. století zjistil Rakouský biolog Reinitzer při zahřívání různých pevných látek až nad bod tání, že vzniklá kapalina je zprvu neprůhledná (opalizuje) a teprve při dalším zahřívání se od jisté teploty změní na průhlednou kapalinu. Stručně řečeno, některé látky mají dva body tání. Se svým pozorováním se svěřil svému příteli fyzikovi Lehmannovi, který se tomuto problému intenzivně věnoval a nazval tyto látky „mezofáze“ (později parakrystaly, kapalné krystaly, tekuté krystaly) . Zjistil, že tyto krystaly lze získat rozpoštěním v rozpouštědle (lyotropní tekuté krystaly), nebo roztavením (termotropní tekuté krystaly).
Příklad tekutých krystalů:
P – azoxyanisol

Oblast výskytu fáze tekutých krystalů: < 357 K – 423 K >.
Ethylester p – anisalaminoskořicové kyseliny

Oblast výskytu fáze tekutých krystalů: < 356 K – 412 K >.
9.4.1. Struktura tekutých krystalů.
Obecně se dá říci, že tekuté krystaly se vyskytují u látek, které mají nesymetrické, protáhlé molekuly, tedy u látek organických. Takové dlouhé molekuly lze uspořádat tak, že jsou uloženy v trojrozměrné krystalové mřížce, uspořádané ve všech třech směrech (pak se jedná o pevnou fázi). Dále je lze uspořádat ve dvou směrech, nebo v jednom směru (to se jedná o tekuté krystaly). Jsou-li neuspořádané, mají strukturu typických kapalin. Proto se přímo nabízí rozdělení tekutých krystalů podle stupně uspořádání na:
a) Nematické tekuté krystaly (název pochází od řeckého slova nema = nit). Tyto tekuté krystaly jsou uspořádány v jednom směru (samozřejmě díky tepelnému pohybu jsou ze svého směru stále vychylovány – Obr.9.13.).

Obr. 9.13. Struktura nematických tekutých krystalů.
b) Smektické tekuté krystaly (smegma = mýdlo). V případě těchto tekutých krystalů existuje uspořádání ve dvou směrech, tj. molekuly jsou uspořádány ve vrstvách (Obr. 9.14a,b,c..). Mezi vrstvami se u lyotropních tekutých krystalů nachází kapalina, v níž jsou rozpuštěny. obrázků je vidět, že podélné osy molekul v jednotlivých vrstvách mohou být orientovány různým směrem. Odtud plyne, že takové krystaly jsou určitě opticky aktivní (stáčejí polarizační rovinu).

Obr.9.14a. Struktura smektických tekutých krystalů.


Obr.9.14.b. Příklad orientace smektických Obr.9.14c. Příklad orientace smektických
tekutých krystalů. tekutých krystalů.
c) Cholesterické tekuté krystaly: Z Obr.9.15. plyne, že cholesterické krystaly jsou uspořádány v jednotlivých rovinách tak, že v každé z nich jsou podélné osy molekul rovnoběžné a v sousedních rovinách jsou vždy trochu pootočené. Cholesterické krystaly jsou opticky aktivní i tenká vrstvička těchto krystalů značně stáčí polarizační rovinu.

Obr.9.15. Cholesterické tekuté krystaly.
d) Diskotické tekuté krystaly: Struktura těchto krystalů připomíná hromádku mincí (molekuly jsou ploché, mají tvar disků).
9.4.2. Vlastnosti a využití tekutých
krystalů.
Významnou vlastností tekutých krystalů je skutečnost, že jsou velmi citlivé na změnu fyzikálních polí (kromě gravitačního), na změnu teploty, chemické látky apod. Tato citlivost se projevuje ve změně struktury a lze ji indikovat opticky (již zmíněným stáčením polarizační roviny, průhledností, barvou apod.). Například citlivosti na teplotu se využívá v lékařství (měření malých změn teploty kůže). Citlivosti na změnu elektrického pole se využívá při konstrukci displejů a obrazovek s tekutými krystaly. Citlivosti na chemické látky se využívá při konstrukci přístrojů, umožňujících měřit přítomnost malého množství různých látek (např kokainu).
Živé organismy jsou ve své postatě tekutými krystaly (rostlinné tkáně, kosti, svaly) a důvodem toho, že život na Zemi vznikl na bázi tekutých krystalů je právě jejich citlivost na změny vnějších podmínek (která je hybnou silou vývoje).
10. Získávání a měření
nízkých tlaků.
Jednotky tlaku:
1 Pa = N / m2
1 at = kp / cm2 =
0,9807.105 Pa (technická atmosféra)
1b = 105 Pa
1 atm = 760 torr = 1,01325.105
Pa (fyzikální atmosféra)
1 torr = 1,3332.102
Pa = tlak 1 mm sloupce Hg.
V dalším budeme
užívat jednotek torr (v této oblasti názornějších a tradičních).
Důvody vytváření
vakua:
-
volný pohyb
částic,
-
odstranění
zejména chemického vlivu plynu při technologických postupech.
10.1. Vývěvy.
10.1.1. Vodní vývěva,
vývěva pístová.
Princip: Bernoulliho rovnice, rovnice kontinuity.


Obr.10.1. Vodní vývěva Obr.10.2. Pístová vývěva.
(R – recipient)
Pístová vývěva.
Princip činnosti:
p1(VR
+ V) = b.VR (1)
odtud
 (2)
(2)
kde VR, resp. V jsou objemy recipientu, resp.
válce vývěvy
Při druhém nasátí
máme pro tlak p2 hodnotu
 (3)
(3)
Po n nasátích
máme tedy
pn=kn.b (4)
Zřeďování je limitováno velikostí škodlivého
prostoru S. Zřeďování plynu v
recipientu ustane v tom okamžiku, jakmile bude tlak recipientu pR právě roven tlaku ve válci, vzniklém rozepnutím části
vzduchu ve škodlivém prostoru (který má při spojení s vnější atmosférou
tlak, rovný b):
 (5)
(5)
Kde VS je objem škodlivého
prostoru a pR je nejnižší
dosažitelný tlak v recipientu (ukazuje se, že to je max. 1 torr). Pro
dosažení vyššího vakua používáme vícestupňových pístových vývěv, nebo rtuťové
vývěvy Geisslerovy, kde je pevný píst nahrazen pístem rtuťovým, který zaplní i škodlivý
prostor.
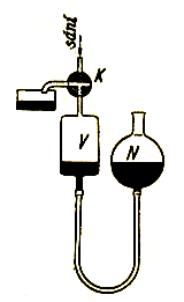
Obr.10.3.
Geisslerova rtuťová vývěva.
10.1.2.
Vývěvy, založené na principu přenosu.
Rotační vývěvy

Obr.10.4. Lopatková
rotační vývěva ( L – lopatka, K – kanálek pro cirkulaci oleje,
O – náplň
oleje, O´- kontrolní okénko, R – rotor, VO – vstupní otvor,
VV – výstupní
ventil, G – vpouštěcí ventil)..
Princip činnosti
těchto vývěv: periodické zvětšování a zmenšování činného prostoru vývěvy. Patří
sem Lopatková vývěva. Rotační olejová vývěva – olej je zde kvůli těsnosti aparatury a
mazání.
Čerpací rychlost rotační vývěvy:
S = f(v + x) (6)
kde f je frekvence otáčení rotoru, v je činný objem a x je škodlivý prostor (prostor pod výstupním
ventilem).
Mezní tlak:
![]() (7)
(7)
b je barometrický tlak.
Jiný typ rotační
vývěvy: Gaedeova rtuťová vývěva

Obr.10.
5. Gaedeova rtuťová rotační
vývěva (1 – plášť, 2 – buben se třemi
komorami, 3
– sací trubice, s – sací otvory v komorách,
4 – sací
buben, 5 – k předčerpacím vývěvám.
Rotační vývěvy s kolujícím rotorem
„kolování“ – rotor se dotýká při svém pohybu
vnitřních stěn v různých místech.
Rotační vývěvy se
konstruují obvykle jako dvoustupňové
Olej do rotačních vývěv: mazání, těsnění – nutná vhodná viskozita a
nízká tenze par. Protože se v něm rozpouštějí čerpané plyny, dochází často
k degradaci oleje a korozi součástek vývěv.

Obr.10. 6. Vývěva s kolujícím rotorem a přepážkou (R – rotor, K –
kanálek pro cirkulaci oleje, VO –
vstupní otvor, V – výstupní ventil, O – osa rotoru, P – posuvná přepážka, S – statorová komora).
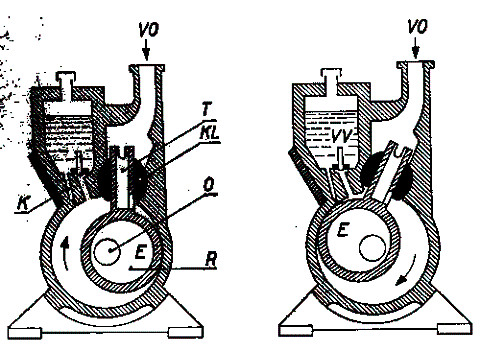
Obr.10.7. Vývěva s kolujícím rotorem a čtyřhrannou trubicí (R – rotor, E – excentr,
O – osa excentru, T – čtyřhranná trubice s otvorem, KL – kloub,
K – kanálek pro cirkulaci oleje, VV – výstupní ventil, VO – vstupní otvor.
Rootsova vývěva
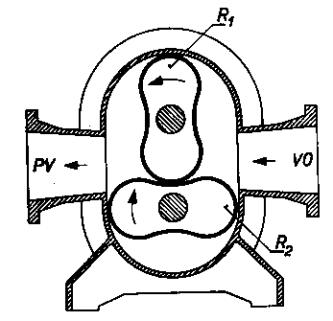
Obr.10.8. Rootsova vývěva (R1, R2 – rotory, PV – výstupní
otvor,
VO – vstupní otvor.
Plyn se v této vývěvě nestlačuje, pouze posouvá. Rotory se o sebe
netřou, není je tedy třeba mazat. Frekvence rotace – až tisíce otáček za
minutu.
Velká čerpací rychlost. Jako předstupeň vyžadují rotační vývěvy. Jsou
citlivé na vniknutí nečistot => jsou nutné filtry (ale tím se sníží čerpací
rychlost).
Mezní tlak: až 10-5 torr (dvoustupňová vývěva)
Turbomolekulární vývěvy

Obr.10.9. Molekulární
vývěva (R – rotor, S – plášť vývěvy).

Obr.10.10. Turbomolekulární
lopatková vývěva s dvěma typy lopatek (R – rotor,
S – stator,
VO – vstupní otvor).
Velká rychlost otáčení rotoru – až 104 ot./min.
Molekuly získají impuls ve směru rotace
Jsou náročné na přesnost opracování součástek a choulostivé
v provozu.
Mezní tlak max. 10-7 torr (nelze je odplynit zahřátím na
vysokou teplotu).
Úpravou rotoru do tvaru kotoučů s lopatkami (statory mají lopatky
orientované naopak) se uvedené nedostatky odstraní, tj. lze je zahřát a
odplynit. Tak lze dosáhnout mezního tlaku až 10-11 torr.
Mají velkou čerpací rychlost, neobsahují olej => žádná tenze par
oleje.

Obr.10.11. Difúzní vývěva (VO – vstupní otvor, T – tryska, KS – kondenzační stěna,
PV –
k pomocné vývěvě, V – varník, K – pracovní kapalina, O – topné
tělísko,. V levé části obrázku je
znázorněna koncentrace čerpaného plynu
na
souřadnici, proložené osou vývěvy).
Difúzní vývěvy
Princip opět stejný – sdílení impulzu mezi molekulami čerpaného plynu a
rychle
se pohybujícím proudem par oleje (nadzvukovou rychlostí).
Páry na vodou ochlazovaných stěnách kondenzují a stékají do varníku.
Kromě oleje se užívá též rtuť (je ale třeba vyšších teplot a aby páry
nevnikaly do čerpaného prostoru, musí být vymrazovány pomocí tekutého dusíku – Langmuirova
rtuťová vývěva).
Mezní tlak pro olejové vývěvy: 10-8 torr.
Pro Hg vývěvy a vývěvy s velmi kvalitními oleji: 10-13
torr.
Obvykle jsou vícestupňové.


Obr.10.12. Langmuirova
rtuťová difúzní Obr.10.13. Dvoustupňová difúzní
vývěva (s – sání, v – připojení vývěva (s – sání,
1, resp.2 -
předčerpací vývěvy). první, resp. druhý
stupeň.
8.1.2.
Vývěvy, založené
na principu vazby molekul v systému.
Molekuly nejsou transportovány mimo vývěvu,
ale jsou v ní vázány.
Proto se užívají jenom při velmi nízkých
tlacích (mají omezenou vazbu molekul).
Kondenzační vývěvy.
Využívají kondenzace plynu na stěnách vývěvy, chlazené kapalným vodíkem, nebo heliem. Molekuly plynu dopadají na stěny, adsorbují se zde a nakonec vytvoří krystalický kondenzát

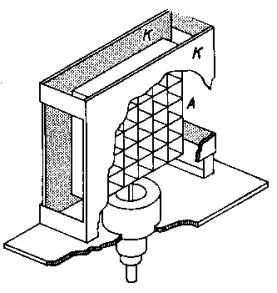
Obr.10.14. Molekulové síto ( Ch – tekutý N2, Obr.10.15. Titanová rozprašovací vývěva.
M – mřížka, TT – topné tělísko, S –
granule ( K – titanové katody, A – mřížková
molekulového síta, VS – k vakuovému
systému. anoda).
Iontově sorpční vývěvy
Využívají chemisorpce molekul na vrstvě
aktivního kovu. Kov se buď vypařuje, nebo katodově rozprašuje.
Vypařovací vývěvy vyžadují značný elektrický
příkon a musí být chlazeny vodou.
Vývěvy rozprašovací (např. titanová): skládá
se ze dvou paralelních titanových deskových elektrod a mezi nimi je roštová
anoda.
Magnetické pole je orientováno tak, aby bylo
kolmé k rovině elektrod. Na anodu se vloží napětí několik kV, takže
vznikne výboj, který rozprašuje materiál elektrod na okolní stěny. Na
rozprášený materiál se váže zbytkový plyn (který je ionizovaný). Lze dosáhnout
tlaku 10-11 – 10-12 torr.
Nevýhoda – je potřebný silný magnet.
Getrování – využití při výrobě elektronek
10.2.
Měření nízkých tlaků.
10.2.1. Rtuťové manometry (Mc Leodův)


Obr.10.16. Mac Leodův Obr.10.17. K objasnění principu činnosti Mac
Leodova
rtuťový manometr. manometru.
Princip činnosti Mc Leodova manometru:
8px.V
= p.v
(8)
p - px
= h.r.g (9)
![]() (10)
(10)
Lze jimi měřit až 10-10 torr.
Membránové manometry
Tyto manometry využívají pružných vlastností membrán (které se prohnou v závislosti na rozdílu tlaku vně a uvnitř prostoru, který rozdělují).

Obr.10.18. Různé tvary nádob membránových manometrů
(měch, krabice, pevná nádobka
s membránou, nádobka spirálního tvaru.
Lze jimi měřit tlak asi do 10-4
torr.
Molekulární manometr (Knudsenův)
Tlak závisí na střední aritmetické rychlosti
molekul a ta je funkcí teploty.
Princip: destička na křemenném vlákně se
zrcátkem. Volná destička A je umístěna mezi dvěma elektrickým proudem
vyhřívanými pevnými destičkami B tak, že se tepelný tlak na destičku A sčítá.
Rozsah měřeného tlaku: 10-2 – 10-7
torr.
Ionizační manometr
Skládá se ze žhavené katody – zdroje elektronů,
které ionizují zbytkový plyn. Množství vzniklých iontů je úměrné hustotě plynu
a tedy i jeho tlaku. Napětí anoda – katoda je 150 V – 200 V. Napětí kolektoru
vůči katodě – 25V až – 50V.
Tlak plynu se určuje z proudu
kolektorem.
Rozsah: 10-3 – 10-8
torr. Po speciálních úpravách: 100 – 10-11 torr.
Langmuirův – Dushmanův manometr
Využívá přenos impulzu zředěným plynem. Dolní
kotouček rotuje a molekuly mezi oběma
kotoučky přenášejí impulz na horní kotouček. Tlak se určuje z úhlu
natočení zrcátka.
Měřící rozsah: 10-2 – 10-8
torr.
Inverzní ionizační manometr.
Princip: žhavená katoda, měří se proud iontů,
dopadajících na kolektor. Proud iontů je však zkreslován proudem fotoelektronů,
které se uvolňují z kolektoru vlivem měkkého rtg. záření, které se uvolňuje
z mřížky, na kterou dopadají elektrony z katody. Při 10-10
torr je kolektorový proud roven asi 10-11A.


Obr.10.19. Molekulární manometr (A – destička Obr.10.20.
Ionizační vakuometr.
se zrcátkem Z, B – vyhřívané
destičky).


Obr.10.21. Langmuirův – Dushmanův Obr.10.22.
Inverzní ionizační
manometr (KZ – zavěšený kotouč se manometr se žhavou katodou.
zrcátkem Z, Kr – rotující kotouč, spojený (M – mřížka, K – katoda,
s osou kotvy K, V – vinutí motoru. kol – kolektor iontů).
Výbojový manometr s magnetickým polem (Penningův)

Obr.10.23. Penningův manometr.
Existuje několik různých typů takových
manometrů.
Ionizační dráha se prodlužuje díky
magnetickému poli.
Jeho elektrody jsou studené, není problém
s odplyněním. Mezi katodami je prstencová, nebo válcová anoda. Kolmo na
osu anody působí magnetické pole, takže elektrony se pohybují po spirále od
jedné katody k druhé a zpět, dokud srážky s atomy plynu nezpůsobí, že
elektrony spadnou na anodu. Množství srážek a tím i doba průletu elektronu mezi
katodou a anodou je dána tlakem plynu. Doba průletu elektronu určuje velikost
proudu mezi katodou a anodou. Měření tohoto proudu určuje tedy tlak.
Napětí mezi K a A je několik kV,
intenzita mag. pole až 104 A / m.
Měřící obor 10-2 – 10-6 torr.
Inverzní výbojový manometr (Redheadův)
Osou válcové katody prochází tyčová anoda
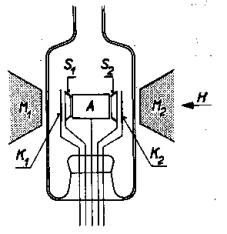

Obr.10.24. Výbojový manometr se stíněním
Obr.10.25. Inverzní výbojový manometr.
(M1 , M2 – pólové
nástavce magnetů, S1, S2 – ( A – tyčová anoda, K – katoda, E -
- stínící elektrody, A – anoda. - stínící elektroda).
Je třeba doplnit stínícími elektrodami (aby
nevznikala autoemise elektronů z katod).
Lze měřit tlak až 10-14 torr.