Subsections
Obrázek:
Histogramy pro různé typy rozdělení
|
Předmětem statistického zkoumání jsou hromadné jevy, to znamená, že
zkoumáme vlastnosti u velkého počtu prvků.
Základní soubor sdružuje tyto prvky.
Počet prvků základního souboru se nazývá rozsah souboru.
Údaje (vlastnosti) uvedené pro prvky základního nazýváme (statistické)
proměnné nebo též znaky.
Většinou je nákladné, nesnadné a nebo dokonce nemožné zjišťovat hodnoty
statistických proměnných pro každý prvek základního souboru. V takovém
případě pracujeme s vhodně zvoleným výběrem (vzorkem) ze základního
souboru. Pokud je výběr vytvořen statisticky správně, například náhodným
výběrem, dá se na jeho základě získat určitá představa o základním souboru.
Při statistických zkoumáních se zaměřujeme na charakterizování a popis
rozdělení četnosti proměnné (znaku), a to jak v základním souboru, tak
i ve výběru. Pod těmito slovy si můžeme představit tabulku, která v jednom
řádku obsahuje hodnoty proměnných a ve druhém odpovídající četnosti (tj.
kolikrát byla tato hodnota obsažena v souboru). U spojitých veličin se
výpisu do tabulky samozřejmě četnost v určitých zvolených mezích (intervalu).
Četnost v tomto případě nepřísluší hodnotám, ale intervalům. Intervalové
rozdělení četnosti se často znázorňuje graficky pomocí histogramu nebo
polygonu četnosti.
Při kreslení histogramu vynášíme na osou x intervaly a na osu y četnosti
v těchto intervalech. Obdélníčky se stranami odpovídajícími intervalu hodnot
a dosažené četnosti vytvoří histogram. Pospojováním středů horních stran
obdélníčků získáme polygon.
Optimální počet intervalů 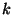 obvykle volíme podle Stugersova pravidla.
obvykle volíme podle Stugersova pravidla.
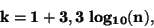 |
(81) |
kde 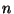 je počet prvků, které máme k dispozici.
Často četnosti nevyjadřujeme absolutně, ale relativně, tj. jako poměrnou část
z celkového rozsahu souboru
je počet prvků, které máme k dispozici.
Často četnosti nevyjadřujeme absolutně, ale relativně, tj. jako poměrnou část
z celkového rozsahu souboru 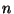 (absolutní četnost dělíme
(absolutní četnost dělíme 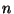 ). Mluvíme pak
o relativním rozdělení četnosti.
). Mluvíme pak
o relativním rozdělení četnosti.
Udávají střed celé skupiny údajů, kolem kterého všechny hodnoty kolísají
(analogie těžiště).
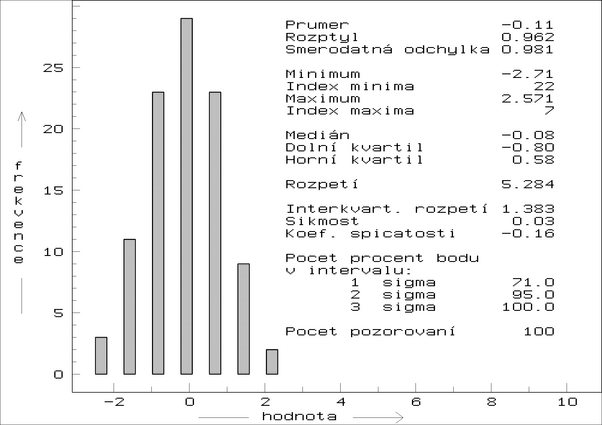
Výběrový (aritmetický průměr) je definován známým vzorcem
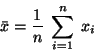 |
(82) |
Medián je definován jako prostřední hodnota výběru, a to prostřední
v pořadí hodnot uspořádaných podle velikosti. Jinak řečeno polovina hodnot
výběru je menší nebo rovna mediánu a polovina hodnot je větší nebo rovna
mediánu. Pokud prostřední hodnota není určena jednoznačně (například pro
sudý rozsah výběru) je za medián brán průměr dvou prostředních hodnot.
Obrázek:
Popisné statistiky dat z histogramu: ukázka možností procedury
Statistiky knihovny STAT.FML
|
|
Modus je nejčetnější hodnota znaku.
Kvantil 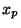 (označovaný někdy jako p-procentní kvantil) je hodnota
znaku, pro který platí, že nejméně p-procent prvků má hodnotu menší nebo
rovnu
(označovaný někdy jako p-procentní kvantil) je hodnota
znaku, pro který platí, že nejméně p-procent prvků má hodnotu menší nebo
rovnu 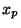 a
a 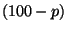 procent prvků je větších nebo rovno
procent prvků je větších nebo rovno 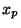 .
.
Používají se tyto kvantily:
| medián |
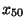 |
| dolní kvartil |
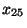 |
| horní kvartil |
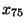 |
| decily |
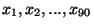 |
| percentily |
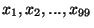 |
Příklad: Jak počítat kvantily si ukážeme na jednoduchém příkladu.
Mějme dána následující čísla: 1, 3, 2, 2, 4, 4, 2, 2, 5, 1, 2, 3.
Čísla uspořádáme vzestupně:
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 1 |
1 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
Protože hodnot proměnných je 12, je medián roven aritmetickému průměru
šesté a sedmé hodnoty:
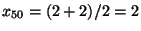
Dolní kvartil je roven třetí hodnotě
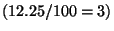 .
.
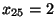
Horní kvartil je roven deváté hodnotě
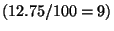 .
.
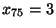 .
.
Modus je roven 2.
Charakteristiky variability udávají koncentraci nebo rozptýlení (variabilitu)
hodnot kolem zvoleného středu skupiny.
Rozpětí R je definováno jako rozdíl největší (maximální) a nejmenší
(minimální) hodnoty.
Mezikvartilové rozpětí je definováno jako rozdíl horního a dolního
kvartilu (je tedy rovno
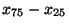 ).
).
Rozptyl 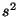 je definován jako součet kvadratických odchylek
od průměru, děleným rozsahem výběru zmenšeným o 1.
je definován jako součet kvadratických odchylek
od průměru, děleným rozsahem výběru zmenšeným o 1.
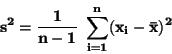 |
(83) |
Směrodatná odchylka s je definována jako odmocnina z rozptylu.
(Průměrná) absolutní odchylka d je definována jako průměr
absolutních odchylek od průměru.
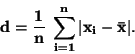 |
(84) |
V porovnání se směrodatnou odchylkou se tolik nezvětšuje při výskytu
extrémních hodnot.
Variační koeficient c slouží k měření relativní variability. Je
definován jako podíl směrodatné odchylky a průměru.
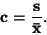 |
(85) |
Využívá se jej také pro porovnání variabilních znaků měřených v odlišných
jednotkách.
Charakteristiky šikmosti udávají, jsou-li hodnoty kolem zvoleného středu
rozloženy souměrně nebo je-li rozdělení hodnot zešikmeno na na jednu stranu.
Všechny charakteristiky šikmosti nějakým způsobem využívají vztahů mezi
průměrem 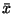 , mediánem
, mediánem 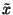 a modem
a modem 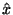 .
.
- Pro záporně sešikmené rozdělení je
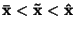
- Pro symetrické rozdělení je
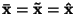
- Pro kladně sešikmené rozdělení je
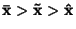
(Momentový) koeficient šikmosti 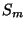 je definován vztahem:
je definován vztahem:
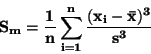 |
(86) |
Kvantilový koeficient šikmosti 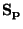 je definován jako
je definován jako
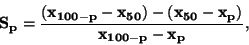 |
(87) |
kde 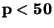
Charakteristiky špičatosti udávají, jaký průběh má rozdělení hodnot kolem
zvoleného středu (rozdělení). Čím je rozdělení špičatější, tím víc jsou
hodnoty soustředěny kolem daného středu rozdělení. Na druhé straně,
rozdělení s nízkou špičatost často obsahuje hodnoty velmi vzdálené od středu
rozdělení.
(Momentový) koeficient špičatosti 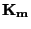 je definován vztahem
je definován vztahem
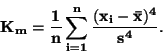 |
(88) |
Někdy se jako charakteristika špičatosti používá veličina 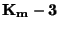 .
Je to proto, že normované normální rozdělení má
.
Je to proto, že normované normální rozdělení má 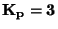 . Při porovnávání
zda
. Při porovnávání
zda 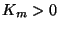 ( nebo původně
( nebo původně 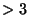 ) zjišťujeme, zda je rozdělení špičatější
(strmější) než normované normální rozdělení.
Kvantilový koeficient špičatosti
) zjišťujeme, zda je rozdělení špičatější
(strmější) než normované normální rozdělení.
Kvantilový koeficient špičatosti 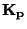 je definován
je definován
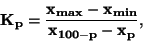 |
(89) |
kde 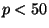 .
. 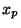 je odpovídající kvantil (např. dolní kvartil
je odpovídající kvantil (např. dolní kvartil 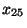 ,
nebo první decil
,
nebo první decil 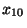 atd.)
Vztah mezi kvantilovým a momentovým koeficientem šikmosti (špičatosti)
je podobný vztahu průměru a mediánu, či rozptylu a kvantilových rozpětí.
Obecně je možno říct, že kvantilové charakteristiky jsou většinou méně citlivé
na velké změny (chyby) v datech (nejsou jimi tolik ovlivňovány). Tato
vlastnost v sobě však může nést i jistou nevýhodu.
atd.)
Vztah mezi kvantilovým a momentovým koeficientem šikmosti (špičatosti)
je podobný vztahu průměru a mediánu, či rozptylu a kvantilových rozpětí.
Obecně je možno říct, že kvantilové charakteristiky jsou většinou méně citlivé
na velké změny (chyby) v datech (nejsou jimi tolik ovlivňovány). Tato
vlastnost v sobě však může nést i jistou nevýhodu.
Popisné statistiky umožňuje provádět i program EXCEL. Možnosti ukazuje
následující tabulka:
| Data |
Název |
Hodnota |
| 4,7 |
střední hodnota |
4,49 |
| 4,4 |
chyba střední hodnoty |
0,0379 |
| 4,5 |
medián |
4,5 |
| 4,6 |
modus |
4,5 |
| 4,4 |
směrodatná odchylka |
0,1197 |
| 4,4 |
rozptyl výběru |
0,0143 |
| 4,3 |
špičatost |
-0,369 |
| 4,5 |
šikmost |
0,233 |
| 4,6 |
rozdíl max-min |
0,4 |
| 4,5 |
minimum |
4,3 |
| |
maximum |
4,7 |
| |
součet |
44,9 |
| |
počet |
10 |
| |
věrohodnost (95 %) |
0,0742 |
© František Šťastný, 1997
![]() ).
).
![]() je definován jako součet kvadratických odchylek
od průměru, děleným rozsahem výběru zmenšeným o 1.
je definován jako součet kvadratických odchylek
od průměru, děleným rozsahem výběru zmenšeným o 1.
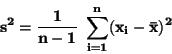
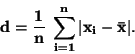
![]() , mediánem
, mediánem ![]() a modem
a modem ![]() .
.
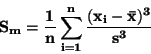
![]() je definován vztahem
je definován vztahem