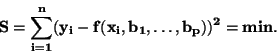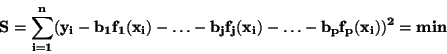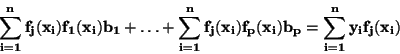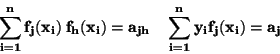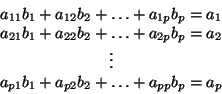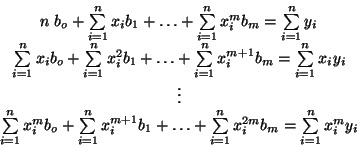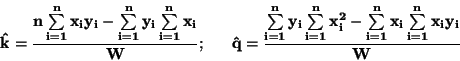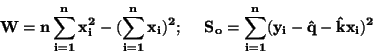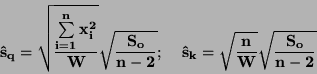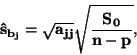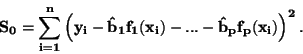Obrázek:
Proložení přímky metodou nejmenších čtverců
|
|
Mějme naměřenou závislost, tj. soubor dvojic
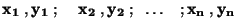
Těmito body proložíme funkci
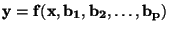 , přičemž
, přičemž
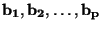 jsou
její parametry, jejichž statistické odhady
jsou
její parametry, jejichž statistické odhady
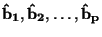 hledáme.
hledáme.
Kritérium: Součet S čtverců odchylek empirických hodnot 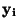 od
vyrovnaných
hodnot
od
vyrovnaných
hodnot
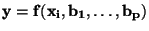 je minimální, tj.
je minimální, tj.
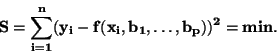 |
(49) |
Nutnou podmínkou existence minima funkce 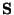 je
je
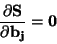 |
(50) |
pro j = 1, 2, ..., p.
Dále omezíme tvar funkce f na lineární regresní funkci
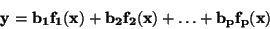 |
(51) |
Podmínka pro minimum má tvar
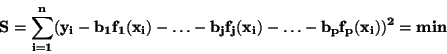 |
(52) |
Konkrétně pro parametr 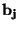 obdržíme
obdržíme
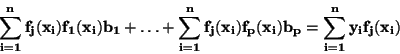 |
(53) |
Označme
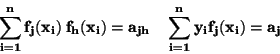 |
(54) |
Získáme tak soustavu rovnic:
Řešením této soustavy tzv. normálních rovnic obdržíme hledané odhady
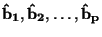
Pro polynom 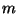 tého stupně
tého stupně
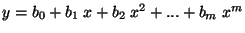 mají rovnice tvar
mají rovnice tvar
Pro příklad prokládání přímky
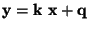 dostaneme toto řešení
dostaneme toto řešení
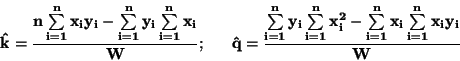 |
(55) |
kde
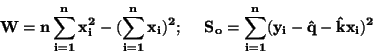 |
(56) |
Pro směrodatné odchylky platí
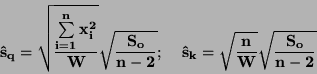 |
(57) |
Z obecných statistických úvah pro standardní odchylku parametru 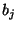 plyne
plyne
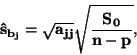 |
(58) |
kde 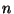 je počet měření,
je počet měření, 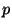 je počet určovaných parametrů,
je počet určovaných parametrů, 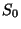 je
zbytkový (reziduální) součet čtverců odchylek
je
zbytkový (reziduální) součet čtverců odchylek
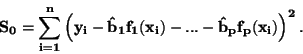 |
(59) |
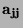 je
je 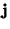 - tý diagonální prvek matice inverzní k matici soustavy
normálních rovnic.
Funkce
- tý diagonální prvek matice inverzní k matici soustavy
normálních rovnic.
Funkce
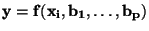 se nazývá teoretická regresní
funkce a její znázornění se nazývá teoretická regresní křivka.
Regresní funkce
se nazývá teoretická regresní
funkce a její znázornění se nazývá teoretická regresní křivka.
Regresní funkce
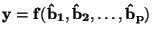 v níž jsou neznámé parametry
v níž jsou neznámé parametry 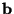 nahrazeny odhady
nahrazeny odhady 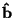 se nazývá
empirická regresní funkce a její grafické znázornění se nazývá
empirická regresní křivka.
se nazývá
empirická regresní funkce a její grafické znázornění se nazývá
empirická regresní křivka.
Poznámka: Dostupné modely v systému FAMULUS 3.5
PRIMKA.FM : Proložení přímky metodou nejmenších čtverců
PRIMKAP.FM: Předcházející program doplněný o analýzu dat
Obrázek:
Proložení přímky metodou nejmenších čtverců s vyznačením
intervalu spolehlivosti
|
|
Obrázek:
Proložení polynomu metodou nejmenších čtverců s vyznačením
intervalu spolehlivosti
|
|
© František Šťastný, 1997