Next: 9 Metoda nejmenších čtverců Up: frst_zed Previous: 7 Chyba nepřímo měřené veličiny Obsah
Pro aritmetický průměr
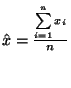 platí
platí
![]() .
.
Protože měření je prováděno za stejných podmínek je
![]() .
.
| (44) |
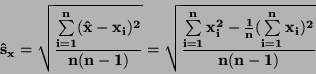 |
(45) |
Má-li měřená veličina normální rozdělení můžeme k výpočtu intervalu
spolehlivosti využít následující věty.
Věta: Nechť
![]() je výběr z normálního rozdělení
je výběr z normálního rozdělení
![]() . Pak náhodná veličina
. Pak náhodná veličina
| (46) |
| (47) |
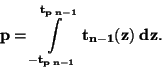 |
(48) |
Tabulka Studentových koeficientů:
| P | 0.050 | 0.100 | 0.200 | 0.500 | 0.683 | 0.900 | 0.954 | 0.980 | 0.990 |
| v | |||||||||
| 1 | 0.079 | 0.158 | 0.325 | 1.000 | 1.839 | 6.314 | 13.815 | 31.821 | 63.657 |
| 2 | 0.071 | 0.142 | 0.289 | 0.816 | 1.322 | 2.920 | 4.500 | 6.965 | 9.925 |
| 3 | 0.068 | 0.137 | 0.277 | 0.765 | 1.198 | 2.353 | 3.292 | 4.541 | 5.841 |
| 4 | 0.067 | 0.134 | 0.271 | 0.741 | 1.142 | 2.132 | 2.858 | 3.747 | 4.604 |
| 5 | 0.066 | 0.132 | 0.267 | 0.727 | 1.111 | 2.015 | 2.640 | 3.365 | 4.032 |
| 6 | 0.065 | 0.131 | 0.265 | 0.718 | 1.091 | 1.943 | 2.508 | 3.143 | 3.707 |
| 7 | 0.065 | 0.130 | 0.263 | 0.711 | 1.077 | 1.895 | 2.421 | 2.998 | 3.499 |
| 8 | 0.065 | 0.130 | 0.262 | 0.706 | 1.067 | 1.860 | 2.359 | 2.896 | 3.355 |
| 9 | 0.064 | 0.129 | 0.261 | 0.703 | 1.059 | 1.833 | 2.313 | 2.821 | 3.250 |
| 10 | 0.064 | 0.129 | 0.260 | 0.700 | 1.053 | 1.812 | 2.277 | 2.764 | 3.169 |
| 11 | 0.064 | 0.129 | 0.260 | 0.697 | 1.048 | 1.796 | 2.249 | 2.718 | 3.106 |
| 12 | 0.064 | 0.128 | 0.259 | 0.695 | 1.044 | 1.782 | 2.225 | 2.681 | 3.055 |
| 13 | 0.064 | 0.128 | 0.259 | 0.694 | 1.041 | 1.771 | 2.206 | 2.650 | 3.012 |
| 14 | 0.064 | 0.128 | 0.258 | 0.692 | 1.038 | 1.761 | 2.189 | 2.624 | 2.977 |
| 15 | 0.064 | 0.128 | 0.258 | 0.691 | 1.035 | 1.753 | 2.175 | 2.602 | 2.947 |
| 16 | 0.064 | 0.128 | 0.258 | 0.690 | 1.033 | 1.746 | 2.163 | 2.583 | 2.921 |
| 17 | 0.064 | 0.128 | 0.257 | 0.689 | 1.031 | 1.740 | 2.153 | 2.567 | 2.898 |
| 18 | 0.064 | 0.127 | 0.257 | 0.688 | 1.029 | 1.734 | 2.143 | 2.552 | 2.878 |
| 19 | 0.064 | 0.127 | 0.257 | 0.688 | 1.028 | 1.729 | 2.135 | 2.539 | 2.861 |
| 20 | 0.063 | 0.127 | 0.257 | 0.687 | 1.026 | 1.725 | 2.128 | 2.528 | 2.845 |
| 21 | 0.063 | 0.127 | 0.257 | 0.686 | 1.025 | 1.721 | 2.121 | 2.518 | 2.831 |
| 22 | 0.063 | 0.127 | 0.256 | 0.686 | 1.024 | 1.717 | 2.115 | 2.508 | 2.819 |
| 23 | 0.063 | 0.127 | 0.256 | 0.685 | 1.023 | 1.714 | 2.109 | 2.500 | 2.807 |
| 24 | 0.063 | 0.127 | 0.256 | 0.685 | 1.022 | 1.711 | 2.104 | 2.492 | 2.797 |
| 25 | 0.063 | 0.127 | 0.256 | 0.684 | 1.021 | 1.708 | 2.100 | 2.485 | 2.787 |
| 26 | 0.063 | 0.127 | 0.256 | 0.684 | 1.020 | 1.706 | 2.096 | 2.479 | 2.779 |
| 27 | 0.063 | 0.127 | 0.256 | 0.684 | 1.020 | 1.703 | 2.092 | 2.473 | 2.771 |
| 28 | 0.063 | 0.127 | 0.256 | 0.683 | 1.019 | 1.701 | 2.088 | 2.467 | 2.763 |
| 29 | 0.063 | 0.127 | 0.256 | 0.683 | 1.018 | 1.699 | 2.085 | 2.462 | 2.756 |
| 30 | 0.063 | 0.127 | 0.256 | 0.683 | 1.018 | 1.697 | 2.082 | 2.457 | 2.750 |
| 31 | 0.063 | 0.127 | 0.256 | 0.682 | 1.017 | 1.696 | 2.079 | 2.453 | 2.744 |
| 32 | 0.063 | 0.127 | 0.255 | 0.682 | 1.017 | 1.694 | 2.076 | 2.449 | 2.738 |
| 33 | 0.063 | 0.127 | 0.255 | 0.682 | 1.016 | 1.692 | 2.074 | 2.445 | 2.733 |
| 34 | 0.063 | 0.127 | 0.255 | 0.682 | 1.016 | 1.691 | 2.071 | 2.441 | 2.728 |
| 35 | 0.063 | 0.127 | 0.255 | 0.682 | 1.015 | 1.690 | 2.069 | 2.438 | 2.724 |
| 36 | 0.063 | 0.127 | 0.255 | 0.681 | 1.015 | 1.688 | 2.067 | 2.434 | 2.719 |
| 37 | 0.063 | 0.127 | 0.255 | 0.681 | 1.014 | 1.687 | 2.065 | 2.431 | 2.715 |
| 38 | 0.063 | 0.127 | 0.255 | 0.681 | 1.014 | 1.686 | 2.063 | 2.429 | 2.712 |
| 39 | 0.063 | 0.126 | 0.255 | 0.681 | 1.014 | 1.685 | 2.061 | 2.426 | 2.708 |
| 40 | 0.063 | 0.126 | 0.255 | 0.681 | 1.013 | 1.684 | 2.059 | 2.423 | 2.704 |
| 41 | 0.063 | 0.126 | 0.255 | 0.681 | 1.013 | 1.683 | 2.058 | 2.421 | 2.701 |
| 42 | 0.063 | 0.126 | 0.255 | 0.680 | 1.013 | 1.682 | 2.056 | 2.418 | 2.698 |
| 43 | 0.063 | 0.126 | 0.255 | 0.680 | 1.012 | 1.681 | 2.055 | 2.416 | 2.695 |
| 44 | 0.063 | 0.126 | 0.255 | 0.680 | 1.012 | 1.680 | 2.053 | 2.414 | 2.692 |
| 45 | 0.063 | 0.126 | 0.255 | 0.680 | 1.012 | 1.679 | 2.052 | 2.412 | 2.690 |
| 46 | 0.063 | 0.126 | 0.255 | 0.680 | 1.012 | 1.679 | 2.051 | 2.410 | 2.687 |
| 47 | 0.063 | 0.126 | 0.255 | 0.680 | 1.011 | 1.678 | 2.050 | 2.408 | 2.685 |
| 48 | 0.063 | 0.126 | 0.255 | 0.680 | 1.011 | 1.677 | 2.049 | 2.407 | 2.682 |
| 49 | 0.063 | 0.126 | 0.255 | 0.680 | 1.011 | 1.677 | 2.047 | 2.405 | 2.680 |
| 50 | 0.063 | 0.126 | 0.255 | 0.679 | 1.011 | 1.676 | 2.046 | 2.403 | 2.678 |
Příklad: Ukázka výpočtu chyby aritmetického průměru pro 10 měření
výšky válečku:
| Výška |
odchylka |
|
| 4,6 | -0,11 | 0,0121 |
| 4,5 | -0,01 | 0,0001 |
| 4,7 | -0,21 | 0,0441 |
| 4,4 | 0,09 | 0,0081 |
| 4,5 | -0,01 | 0,0001 |
| 4,6 | -0,11 | 0,0121 |
| 4,4 | 0,09 | 0,0081 |
| 4,4 | 0,09 | 0,0081 |
| 4,3 | 0,19 | 0,0361 |
| 4,5 | -0,01 | 0,0001 |
| 44,9 | 0,129 |
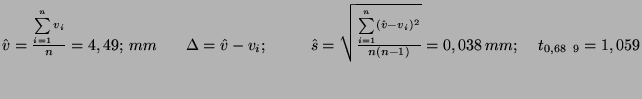
Příklad: Délka byla měřena 6 krát a výsledek měření je uveden takto:
![]() mm. S úrovní spolehlivosti 0,980. Zapište výsledek měření
pro úroveň spolehlivosti 0,683.
mm. S úrovní spolehlivosti 0,980. Zapište výsledek měření
pro úroveň spolehlivosti 0,683.
![]() ,
, ![]() ,
,
![]() .
Protože
.
Protože
![]() je
je
![]() mm.
mm.
Pro ![]() je Studentův koeficient
je Studentův koeficient
![]() .
.
Výsledek je možno napsat ve tvaru
![]() mm.
mm.
© František Šťastný, 1997