Next: 6 Výběrový rozptyl Up: frst_zed Previous: 4 Náhodné vektory Obsah
Chyby měření podle místa vzniku dělíme do čtyř základních skupin:
V literatuře se setkáme s různým způsobem zavedením pojmu chyba
měření, což začátečníkům komplikuje orientaci v problematice.
Často se chyba měření ![]() definuje jako odchylka výsledku měření
definuje jako odchylka výsledku měření
![]() od skutečné hodnoty měřené veličiny
od skutečné hodnoty měřené veličiny ![]() tj.
tj.
![]() .
Definice je sice názorná, ale přesně vzato, je takováto chyba v praxi
použitelná jen v případě, že provádíme měření na standardu a známe,
skutečnou hodnotu měřené veličiny.
V
.
Definice je sice názorná, ale přesně vzato, je takováto chyba v praxi
použitelná jen v případě, že provádíme měření na standardu a známe,
skutečnou hodnotu měřené veličiny.
V ![]() je chyba zavedena takto: Výsledkem každého měření je náhodná
veličina, která obsahuje kromě informace také šum, tj. chyby měření.
Velikost chyby měření je kritériem kvality procesu měření nebo měřícího
přístroje.
Častěji se setkáváme se "statistickou definicí" chyby měření
Je-li x' výsledek měření a
je chyba zavedena takto: Výsledkem každého měření je náhodná
veličina, která obsahuje kromě informace také šum, tj. chyby měření.
Velikost chyby měření je kritériem kvality procesu měření nebo měřícího
přístroje.
Častěji se setkáváme se "statistickou definicí" chyby měření
Je-li x' výsledek měření a ![]() je chyba tohoto měření odpovídající
míře jistoty
je chyba tohoto měření odpovídající
míře jistoty ![]() , pak skutečná hodnota měřené veličiny leží s pravděpodobností
, pak skutečná hodnota měřené veličiny leží s pravděpodobností
![]() v intervalu x'
v intervalu x'
![]() .
Ve fyzice bývá zvykem volit buď
.
Ve fyzice bývá zvykem volit buď ![]() a pak mluvíme o střední kvadratické
chybě nebo
a pak mluvíme o střední kvadratické
chybě nebo ![]() a pak mluvíme o krajní chybě měření.
V technické praxi se často setkáme s tím, že z manuálu přístroje není
zřejmé jaké
hodnotě
a pak mluvíme o krajní chybě měření.
V technické praxi se často setkáme s tím, že z manuálu přístroje není
zřejmé jaké
hodnotě ![]() , uvedená chyba odpovídá. Většinou však má výrobce na mysli
chybu krajní. V praxi je také velice obtížné rozlišit systematickou
a nahodilou složku chyb přístrojů.
, uvedená chyba odpovídá. Většinou však má výrobce na mysli
chybu krajní. V praxi je také velice obtížné rozlišit systematickou
a nahodilou složku chyb přístrojů.
Například v ČSN 35 6505 ze dne 9.4. 1975 je uvedeno:
Chyba - číselně vyjádřený rozdíl mezi údajem přístroje a skutečnou
hodnotou měřené veličiny. U přístrojů, které jsou zdrojem elektrické
veličiny, je chyba rozdíl mezi skutečnou a jmenovitou, indikovanou
a nastavenou hodnotou.
Poznámka:
1. Skutečná hodnota je hodnota, která se zjistí při měření bez chyb.
2. Protože se v praxi skutečná hodnota nedá určit měřením, používá se
místo skutečné hodnoty smluvená skutečná hodnota, která se skutečné
hodnotě blíží (s ohledem na chybu, která se má určovat). Tuto hodnotu
lze získat navázáním na národní etalon.
Absolutní chyba - chyba vyjádřená číselně v jednotkách měřené nebo
vytvářené veličiny.
Poměrná chyba (relativní) - poměr absolutní chyby ke skutečné hodnotě
měřené veličiny.
Chyba vyjádřená v procentech - poměr absolutní chyby ke skutečné hodnotě,
vyjádřené v procentech.
Vztažná hodnota - hodnota, ke které se vztahuje chyba vyjádřená
v procentech.
Základní chyba - chyba stanovená v referenčních podmínkách.
Přídavná chyba - chyba stanovená v podmínkách, kdy jedna z ovlivňujících
veličin zaujímá libovolnou hodnotu v mezích jmenovitého rozsahu používání,
přičemž všechny ostatní ovlivňující veličiny se nacházejí v referenčních
podmínkách.
Poznámky:
1. Při udávání přídavné chyby se základní chyba neuvažuje
2. Použije-li se pro vyjádření přídavné chyby tohoto výrazu ve jmenovitých
poracovních podmínkách, zahrnuje se do této chyby i základní chyba.
Chyba stálosti (stabilita) - chyba v indikované hodnotě nebo hodnotě
vytvářené přístrojem během stanovené doby, přičemž ostatní podmínky se
nemění.
Meze chyb - maximální hodnoty chyb uvedené výrobcem pro jakýkoliv parametr
přístroje ve stanovených podmínkách (referenčních, jmenovitých,
pracovních apod.)
Naměřená hodnota - údaj odečtený na přístroji; je uváděn jako součin
číselné hodnoty a jednotky měřené veličiny.
Referenční podmínky - souhrn podmínek nebo rozsahů pro parametry a ovlivňující
veličiny, při kterých údaj přístroje splňuje ustanovení o dovolených chybách,
při kterých se u přístroje ověřuje základní chyba nebo se přístroje
nastavují.
Jmenovitý rozsah použití - rozsah hodnot ovlivňujících veličin, ve
kterém přístroj splňuje požadavky na chyby ve jmenovitých pracovních
podmínkách.
Jmenovité pracovní podmínky - souhrn pracovních hodnot, rozsahů, parametrů
a ovlivňujících veličin, v jejíchž rozmezí jsou udány technické vlastnosti
přístroje.
Doba náběhu přístroje - doba po zapnutí přístroje potřebná k tomu, aby
přístroj dosáhl vlastností udávaných výrobcem.
Chyby měření se uvádějí číselnými hodnotami:
Pokud provádíme měření na standardu se známou hodnotou ![]() , je možné při
každém opakovaném měření
, je možné při
každém opakovaném měření
![]() stanovit celkovou chybu měření
podle vztahu
stanovit celkovou chybu měření
podle vztahu
![]() . Pokud nejsou v datech hrubé chyby,
je průměrná hodnota chyby měření
. Pokud nejsou v datech hrubé chyby,
je průměrná hodnota chyby měření
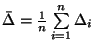 odhadem její
systematické složky a rozdíl
odhadem její
systematické složky a rozdíl
![]() je odhadem náhodné
složky chyby měření. Kromě průměrné chyby
je odhadem náhodné
složky chyby měření. Kromě průměrné chyby ![]() se používá
střední kvadratická chyba definovaná vztahem
se používá
střední kvadratická chyba definovaná vztahem
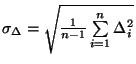 .
Pokud je
.
Pokud je
![]() , považuje se
, považuje se ![]() za průměrnou náhodnou
chybu měření.
Systematické a náhodné chyby souvisejí s pojmy přesnost a správnost měřících
přístrojů:
Přesnost přístroje je definována jako rozmezí statistické nejistoty
výsledků. Souvisí s náhodnými chybami a odpovídá reprodukovatelnosti měření.
Vyjadřuje se jako rozptyl kolem střední hodnoty n-tice naměřených výsledků.
Správnost přístrojů udává průměrnou vzdálenost výsledků měření od
skutečné hodnoty a souvisí se systematickými chybami. Odpovídá odchýlení
průměrné hodnoty výsledku měření od teoretické hodnoty.
Zatímco přesnost lze odhadnout na základě statistické analýzy opakovaných měření,
správnost je nutno stavovat s využitím standardů nebo více přístrojů.
Názorně je to vidět na následujícím obrázku:
za průměrnou náhodnou
chybu měření.
Systematické a náhodné chyby souvisejí s pojmy přesnost a správnost měřících
přístrojů:
Přesnost přístroje je definována jako rozmezí statistické nejistoty
výsledků. Souvisí s náhodnými chybami a odpovídá reprodukovatelnosti měření.
Vyjadřuje se jako rozptyl kolem střední hodnoty n-tice naměřených výsledků.
Správnost přístrojů udává průměrnou vzdálenost výsledků měření od
skutečné hodnoty a souvisí se systematickými chybami. Odpovídá odchýlení
průměrné hodnoty výsledku měření od teoretické hodnoty.
Zatímco přesnost lze odhadnout na základě statistické analýzy opakovaných měření,
správnost je nutno stavovat s využitím standardů nebo více přístrojů.
Názorně je to vidět na následujícím obrázku:
=1.00mm
![\begin{picture}(140.34,60.34)
\put(9.90,49.81){\line(1,0){129.63}}
\put(9.90,3...
...
\put(9.67,5.33){\makebox(0,0)[lc]{Posouzení opakovaných měření}}
\end{picture}](img191.png)
© František Šťastný, 1997