Strojopisnou, ofsetem tištěnou předlohu oskenovala a text softwarově rozeznala Michaela Hanousková, počítačové rozpoznání textu částečně a minimální značkování přidal Jan Hollan.

Pracovní pomůcka – první příklad – pro úvahy o plnohodnotném elektronickém zpřístupnění série seminárních materiálů z celé série seminářů

OS Pedagogická fyzika FVS JČSMF a kateder fyziky někdejší UJEP, nyní MU

Faximile předlohy s podloženým softwarově rozeznaným textem bez korektur viz jiný pdf soubor.

…........................................................................................................

PEDAGOGICKO-FYZIKÁLNÍ DIALOGY

Skalský dvůr u Bystřice nad Pernštejnem, 15.-18. září 1986

DIALOGY 5

OS Pedagogická fyzika FVS JČSMF Katedry fyziky UJEP

Brno, říjen 1986

PEDAGOGICKO-FYZIKÁLNÍ DIALOGY

Skalský dvůr u Bystřice nad Pernštejnem, 15. - 18. září 1986

DIALOGY

5

Redakce:

M. Černohorský

M. ­Fojtíková

J. Janás

OS Pedagogická fyzika FVS JČSMF

Katedry fyziky UJEP

Brno, říjen 1986

PŘEDMLUVA

Skalskodvorská seminární jednání byla tak obsažná, že uskutečnění původně ohlášená představy o shrnutí jejich průběhu a výsledků do jedné brožury obvyklého rozsahu by nemohlo splnit požadavek řádné dokumentace. Rozdělujeme proto závěrečné materiály do dvou částí. Do těchto Dialogů 5 zařazujeme především plné znění stěžejního vystoupení akademika Delonga. Pochopení jeho významu, daleko překračujícího navyklou míru vidění skutečnosti, by nemělo být nad naše možnosti.

Několikerý pohled na seminář v úvodních slovech k němu (M. Černohorský, J. Kučírek, I. Šantavý) zkratkovitě připomíná jeho koncepci, ilustrovanou výběrovými texty J. Bičáka a B. Velického (fyzika a její didaktika), Z. Horského (fyzika a její historie), J. Langera (sepětí fyziky a kultury) a J. Komrsky (portrét fyzikální osobnosti). Experimentální složky fyzikálního vzdělávání v Dialozích 5 zastoupeny nejsou, jsou zařazeny spolu se zprávami z pracovních skupin a ostatní dokumentací do Dialogů 6.

Ukázkami propagovaného stylu seminární práce jsou reakce J. Novotného a V. Freie na předseminární a seminární diskuse. Přiřazená informace E. Adlerové o Evropské fyzikální společnosti je pobídkou naší didaktice fyziky k účinnější mezinárodní aktivitě.

Redakční zpracování materiálů pro závěrečné Dialogy 6 bude dokončeno v nejbližších týdnech. Pokusíme se o jejich vytištění a rozeslání ještě v tomto roce.

Za redakci Dialogů

M. Černohorský

V Brně dne 30. září 1986

ÚVODNÍ SLOVA K SEMINÁŘI

Martin Černohorský

Odborná skupina Pedagogická fyzika fyzikální vědecké sekce JČSMF

Kolegyně a kolegové, vážení hosté,

vítám Vás všechny na semináři Pedagogicko-fyzikální dialogy, který pořádá odborná skupina Pedagogická fyzika Fyzikální vědecké sekce Jednoty československých matematiků a fyziků, katedra obecné fyziky přírodovědecké fakulty a katedra didaktiky fyziky a technické výchovy pedagogické fakulty Univerzity Jana Evangelisty Purkyně v Brně. Za katedry fyziky zahájí náš seminář doc. Kučírek, za Jednotu československých matematiků a fyziků doc. Šantavý.

Jan Kučírek

Katedra obecné fyziky přírodovědecké fakulty UJEP
Katedra didaktiky fyziky a technické výchovy pedagogické fakulty UJEP

Vážené a milé kolegyně, vážení kolegové, vážení přátelé,

zahajuji jednání semináře „Pedagogicko-fyzikální dialogy“, který pořádá odborná skupina Pedagogická fyzika Fyzikální vědecké sekce JČSMF spolu s katedrou obecné fyziky přírodovědecké fakulty a katedrou didaktiky fyziky a technické výchovy pedagogické fakulty brněnské Univerzity Jana Evangelisty Purkyně.

Všichni víme, že semináře, organizované OS Pedagogická fyzika naší Jednoty, anebo, když rozšifrujeme tuto zkratku, semináře, jejichž duší a hnací silou je doc. Martin Černohorský, jsou akce, na které se dlouho těšíme, jsou to akce, o kterých jsme v dostatečném předstihu perfektně informováni, akce, na které se v rámci publikovaných předseminárních materiálů můžeme dobře předem připravit tak, abychom krátký čas jednání té které skupiny nebo podskupiny mohli nejlépe a nejracionálněji využít. Víme, že tyto semináře doc. Černohorského jsou akce, kde se schází spousta zajímavých lidí, nejenom fyziků, se kterými je užitečné diskutovat anebo vyměnit třeba jenom pár slov. Víme, že tyto semináře doc. Černohorského jsou doprovázeny zajímavými kulturně-fyzikálními akcemi a že se konají obvykle ve velmi krásném prostředí Jihomoravského kraje. Máme tedy dostatek důvodů pro to, abychom se nedočkavě těšili, co nám organizátoři přichystali letos ve Skalském dvoře.

Nahlédnutím do programu vidíme, že námětová šíře našeho semináře je obrovská. Program vyžaduje od nás, účastníků, maximální koncentraci podloženou předběžnou přípravou podle publikovaných materiálů, maximální disciplinovanost při dodržování termínů jednání i při formulaci myšlenek, které by měly být prezentovány ve sděleních o práci jednotlivých skupin. Naše rokování, přes tuto námětovou šíři, si uchovává potřebnou tematickou jednotu. Tu vidím v tom, že chápe fyziku a vyučování fyzice jako nedílnou součást kultury národa.

Nahlédnutí do programu nás přesvědčuje také o tom, že úspěch a zdar celého jednání máme každý z nás ve svých rukou. Program přímo vybízí každého účastníka k tomu, aby vyjádřil svůj názor, svoje mínění, aby se vyslovil k základním tezím jednotlivých programových okruhů a aby při schvalování závěrů měl dobrý pocit, že v nich je vložena i jeho idea, jeho názor, jeho myšlenka.

Přeji, aby se zdařil úmysl organizátorů, aby čas, který společně strávíme v tomto příjemném prostředí, byl účelně a smysluplně využit a aby každý z nás rád na Skalský dvůr a pedagogicko-fyzikální dialogy v něm dlouho a rád vzpomínal.

Ivan Šantavý

Předsednictvo Jednoty československých matematiků a fyziků

Vážení přítomní,

dovolte, abych Vám tlumočil pozdrav a přání úspěšného jednání předsednictva hlavního výboru Jednoty československých matematiků a fyziků. Odborná skupina Pedagogická fyzika má jakési singulární postavení v Jednotě, a sice tím, že je organizována jako pedagogická fyzika v rámci Fyzikální vědecké sekce. Vyplňuje svojí činností a svojím programem mezeru, která vznikla a která se dlouho udržovala vzhledem k tomu, že fyzici v Jednotě jsou organizováni jednak ve Fyzikální vědecké sekci, jednak ve Fyzikální pedagogické sekci, přičemž Fyzikální pedagogická sekce se tradičně orientuje na pedagogické otázky nižších stupňů škol až do škol středních včetně.

Odborná skupina Pedagogická fyzika se zabývá zejména pedagogickými problémy spojenými s výukou fyziky na vysokých školách a s fyzikálním vzděláváním obecně. Docent Kučírek tady hovořil velice podrobně a zasvěceně o tradici – dnes už můžeme říct o tradici – seminářů, které pořádá tato skupina ve spolupráci s oběma jmenovanými katedrami brněnské univerzity, a já bych k tomu jen dodal, že při minulých seminářích jsme získali nejen odborné poznatky a nakonec si odvezli materiály předseminární a získali i materiály poseminární, kterých můžeme užít; a že se sem rádi všichni vracíme přesto, že organizátoři sice vlídně a velice společensky, ale zato tím neúprosně ji tlačí všechny k tomu, aby byli aktivní a aby nezůstalo jenom na debatách a slovech, nýbrž aby došlo k určitým zcela konkrétním závěrům, které se zachytí a které budou k dispozici nejen účastníkům, ale všem, kdo o to mají zájem. Přitom ze své zkušenosti, a myslím i ze zkušenosti většiny z vás, si myslím, že jsme se ani v odborné ani ve společenské části nikdy nenudili. Tomuto semináři přeji, aby tomu bylo tak i dnes.

M. Černohorský: Děkuji oběma představitelům pořádajících institucí. Kolegyně a kolegové, přicházíme na seminář každý s dvojím záměrem: něco mu dát a něco z něho získat. To první se už dílem stalo tím, co známe z Dialogů 1 až 4 a co poznáme v seminární knihovně, dílem se ještě stane tím, co předložíme v pracovních skupinách, co předvedeme v demonstracích a co ze sebe vydáme ve shrnujících diskusích. To druhé, co z něho získáme, to bude dáno tím, co si z programu vybereme. Výběr musí být dvojí. Celodennímu intenzivnímu psychickému zatížení od časného rána do pozdního večera ve více než jednom dni je třeba čelit tím, že si každý podle svého zájmu sám upraví a vybere svůj individuální program se zařazením dostatečného odpočinku. Rovněž podle svého zájmu je třeba si vybrat, pracuje-li se na několika místech současně.

Svědčí o organizačních zkušenostech a pochopení vás všech, že ve svých reakcích na program jste nepožadovali úpravy, které by někomu osobně přišly jistě velice vhod, zároveň by však znevýhodnily řadu jiných. Spontánně vzniklé rozdělení do pracovních skupin nerespektuje samozřejmě ekvipartiční princip, ale výsledky skupiny budou záviset ani ne tak na počtu účastníků, jako na závažnosti a promyšlenosti tezí, s nimiž jejich členové do práce vstupují. Tezí na našem semináři rozumíme v souladu s významem tohoto termínu stručně vyjádřené tvrzení. Moderátoři budou v zájmu konkrétnosti a úrovně výsledku práce skupiny nepochybně klást důraz na dodržování seminárních propozic. Projednávání příspěvku zařazeného do skupiny zahájí ne jeho opakováním, ale přímo diskusí k němu po velice stručném jedno- až dvouminutovém uvedení samotným autorem.

Snad bych to ani nemusel číst z té strany D4/274, ale pro jistotu přece:

Jednání každé ze skupin A1 až A9 má přinést konkrétní písemně formulovaný výsledek především k bodu 2, který v plném znění zní: názory k vymezení diskutovaných pojmů a příklady dobře použitelné při jejich zavádění. Problematiku je možno vymezit velmi úzce, ale v každém případě tak, aby se formulovaný výsledek týkal konkrétního příkladu, jak pojem na zvoleném stupni fyzikálního vzdělávání budovat, resp. zavádět. Podle okolností se skupina zaměří i na jiná témata podle vlastní volby v rámci bodů 3 a 4. Avšak i zde je třeba, aby každé téma bylo uzavřeno písemně formulovaným výsledkem, pedagogicko-fyzikálně závažným, a podle možnosti i obecně zajímavým. Zpráva každé skupiny bude otištěna v Dialozích 5.

Rovněž jednání středečních skupin B1 až B10 má přinést konkrétní, písemně formulované výsledky. Výběrová tematika je velmi široká a dává možnost zabývat se jak demonstracemi při výuce a praktiky, tak metodikou fyzikální práce v praxi. Záleží na skupině, jaká konkrétní témata si po ukončení úvodní diskuse k příspěvkům v dalším jednání zvolí. V každém případě je třeba dbát na jasné vymezení tématu a písemnou formulaci výsledku k němu. Zprávy každé skupiny budou otištěny v Dialozích 5.

Náš seminář není zmocněn k nějakému ukládání úkolů institucím a jednotlivcům. Myslím ale, že je kompetentní formulovat požadavky na kompetentní instituce a kompetentní jednotlivce. My samozřejmě nemůžeme zajistit kvalifikovanost činnosti těchto institucí a těchto jednotlivců, ale rozhodně můžeme my sami postupovat tak, aby vlastní práce našeho semináře požadavkům kvalifikovanosti plně dostála a aby to bylo vidět z průběhu všech jeho dílčích částí i plenárních jednání, a nakonec i z Dialogů 5, které budou dokumentací jeho průběhu a výsledků. Záleží samozřejmě na nás všech, abychom s těmito výsledky mohli být alespoň my sami právem spokojeni.

CO CHYBÍ SOUČASNÉ VYSOKÉ ŠKOLE VE VÝCHOVĚ TVŮRČÍCH PRACOVNÍKŮ

Armin Delong

Ústav přístrojové techniky ČSAV 612 64 Brno, Královopolská 147

Vážené kolegyně, vážení kolegové,

s velkou pravděpodobností Vám neřeknu nic nového. Chtěl bych však, aby to, co všichni víte, zaznělo v podobě ničím nepřikrášlené, chtěl bych, na základě svých celoživotních zkušeností, na několika příkladech ukázat, že odpověď na nejožehavější otázku, která je s tématem mého příspěvku spojena, tj. otázku, máme-li vůbec v našich národech talenty, je možné jednoznačně formulovat: máme. Pečujeme však o ně, vzděláváme je s péčí, jakou nezbytně potřebují, dáváme jim možnosti plného uplatnění? Zdá se mi, že i teď můžeme odpovědět jednoznačně: nikoliv. A nic na tom nezmění výjimky. Všeobecná skutečnost je skličující, vyvolávající obavy z dalšího zaostávání za světovým vývojem. Už předem bych chtěl zdůraznit, že si nemíním postěžovat a dovolávat se Vašeho souhlasu, a pak se rozejít. Myslím, že je nejvyšší čas, abychom upozornili na vážnost situace, a já se k tomuto úkolu hlásím a dávám k dispozici především své zkušenosti, které zformulovány mohou a musí být respektovány, není v nich nic ze zbožných přání, která často zaznívají v příspěvcích na různých úrovních, která však s objektivní skutečností nemají nic společného. Co znamenají kupř. formulace „účinněji aktivizovat studenty, rozvíjet zdravou soutěživost a kolektivní práci, vytvářet mezi studenty atmosféru nesmiřitelnosti s nezájmem, nedisciplinovaností a průměrností, vytvořit tak hráz pronikání formalismu a sebeuspokojení do studia naší mládeže“? K čemu je tento návod?

Myslím, že se na problém přípravy vysokoškoláků a mezi nimi talentů musíme dívat na základě řady faktů, které lze stěží popřít, neboť se s nimi setkáváme dnes a denně, znepokojují nás, berou nám chul, abychom se postupně s nimi smířili, abychom nakonec uvěřili, že to vlastně ani jinak nejde. Pokusím se teď zformulovat situaci, jak se mně v současné době jeví, aby na základě této analýzy bylo možně formulovat požadavky, jejichž splnění by vedlo k žádoucí změně.

Jedním ze základních předpokladů úspěšné výchovy tvůrčích pracovníků je jejich bezprostřední účast na tvůrčí práci jejich učitelů, Není jiná metoda. Z tohoto poznatku vyplývá jednoduchý závěr: bezpodmínečným požadavkem musí být nadále vědecká práce vysokoškolských učitelů na úrovni, řeknu to jednoduše, umožňující dosahování výsledků, které by snesly kritéria světovosti (kupř. publikací v renomovaných časopisech apod.). Jaká je skutečnost. Tento požadavek není dělil dobu vůbec uplatňován (zrušili jsme přece habilitační řízení). Místo toho zůstávají požadavky na kvalitní pedagogickou práci. Ale kdo je kvalitní pedagog na vysoké škole? Aniž bych chtěl podceňovat význam pedagogiky, musím zdůraznit, že pro výchovu talentů je nesporně významnější vědecká erudice špatného pedagoga než pouhé, byt vynikající pedagogické schopnosti. Ty jsou bezesporu zapotřebí pro přípravu celé řady pracovníků, u nichž není prvořadým požadavkem schopnost pracovat tvůrčím a koncepčním způsobem, ale na vysoké profesionální úrovni řešit sice náročné a složité, ale přece jen rutinní úkoly.

Z tohoto základního požadavku vyplývá samozřejmě druhý požadavek: Vytvoření materiálních podmínek k vědecké práci (mám na mysli samozřejmě fyzikální výzkum, jsou možná obory u nás, kde materiální podmínky nejsou prvořadým problémem). Tento požadavek se mi zdá jako prvořadý, a to hned z několika důvodů: Materiální a přístrojové vybavení, počítačová technika různého určení, možnosti realizovat speciální experimentální techniku přímo a rozhodujícím způsobem ovlivňují možnosti, a tím výsledky. Skoro bych řekl, že teprve experimentální vybavení na úrovni může vytvořit síto, které by umožnilo oddělit talentované od netalentovaných. Jaká je skutečnost? Jistě budete se mnou souhlasit, že velmi zlá, bez zřejmých možností situaci výrazně změnit. Zdá se tedy, že bude zapotřebí řešit tuto problematiku především. Prvním úkolem by mělo být zjištění, co chybí každé katedře, aby se v průměru přiblížila úrovni ve vyspělých zemích třeba západní Evropy. Obávám se, že dojdeme k závratným sumám, přičemž ve velké většině nebudou moci být technickomateriální prostředky zabezpečeny v socialistických zemích. Jinou možnost opravdu nemáme, než vybudovat potřebnou experimentální základnu. Ve sportu se tato zásada uznává beze zbytku: chceme-li se vyrovnat ostatním, musíme mít stejné podmínky a prostředky. Jenom nadšení je zcela nedostatečné. Ve vědě a technice se občas vyskytují pokusy pomocí apelování na iniciativu a nevím co ještě, nahradit nenahraditelné. V minulých dnech jsem byl na světovém kongresu elektronové mikroskopie v Japonsku. Součástí byla výstava, prvních experimentálních zařízení – elektronových mikroskopů realizovaných v Japonsku. S trochou nostalgie jsem postál před mikroskopem realizovaným v roce 1948, tedy v době, kdy jsme začínali i my. Dnes na univerzitě v Nagoi realizují projekty 5 MeV elektronového mikroskopu s náklady, jejichž výška je pro naše poměry závratná. A přitom je to projekt bezesporu čistě vědecký. Všechno, co jsme doposud na tomto poli realizovali, je zcela nesrovnatelné s tímto jediným projektem.

Příslušné vybavení je nezbytné také proto, aby vysoké školy zaujaly to postavení, které musí mít, postavení instituce, která je v popředí vědeckého a technického pokroku, která vytváří nezbytný předstih. Současná špatná vybavenost vysokoškolských pracovišť postavila odbornou činnost na vysokých školách do polohy tzv. pomoci praxi: rozuměj řešení nepodstatných problémů, tak jak je přináší potřeba průmyslu, který si lacino, za pomoci politického hesla, jehož původní význam byl ochotně modifikován, řeší své problémy. Vysoká škola do této činnosti vkládá minimum: její myšlenkový potenciál bohatě stačí na vyřešení průmyslových trablů, které nejsou nijak zvlášť složité s ohledem na současnou úroveň naší výroby, průmysl je spokojený, plní se politická směrnice. Ale potřebný poznatkový zdroj se tak nevytváří, systematicky se nepracuje, řeší se úkoly ad hoc. A opět argumentace je jednoduchá, ale i správná: s tím, co mají vysoké školy k dispozici, mohou dělat právě jen to, co dělají. Jednoznačně se to obráží i v plánu základního výzkumu i v komplexním programu vědeckotechnického rozvoje, kde je účast našich vysokých škol z pochopitelných důvodů zcela minimální.

Jaké jsou cesty z této situace? Podle mého názoru musí být zmobilizovány všechny společenské zdroje, aby bylo dosaženo rozhodujícího obratu. Musí být dobudovány vysokoškolské areály tam, kde byly před mnoha lety naplánovány a dosud jejich realizace nebyla ani zahájena. Musí být vybudovány moderní laboratoře. Chceme po studentech, aby ve zdech budov, které by dávno dosloužily i původním institucím, věřili, že je to s jejich nezastupitelným významem pro další rozvoj společnosti míněno vážně. Ale tady s oblastí víry zřetelně neuspíváme a také neuspějeme. Tyto prostředky musí být získány třeba na úkor další výstavby průmyslové základny, která při nízkém využití prostorů i prostředků (směnnost 1,2) není bez vyspělé vědeckovýzkumné základny stejně schopna výraznějšího postupu kupředu. Nechci uvádět známé příklady z průmyslově vyspělých kapitalistických zemí, kde se podílejí na vybudování a provozu vědeckovýzkumných center i navzájem si konkurující firmy. U nás se často podpora redukuje na darování vyřazených prostředků z výroby. To ovšem opravdu není pro studenty dobré; mají-li být připravováni pro budoucnost, a pro výchovu talentů to platí obzvláště, musí pracovat na významných problémech, které jsou v popředí zájmu světové vědy, a technickými možnostmi, které musí být srovnatelné s možnostmi a prostředky našich soupeřů. Jiná cesta neexistuje, jiné cesty jsou iluzorní.

Možná, že se Vám bude zdát, že tomuto problému věnuji příliš mnoho pozornosti. Chci Vás však ubezpečit, že mé celoživotní zkušenosti ukazují, že je to conditio sine qua non. Hráli bychom si jenom na schovávanou, kdybychom tvrdili, že materiální zabezpečení není jedním z nejdůležitějších předpokladů výchovy tvůrčích pracovníků. Ještě jeden aspekt má totiž tento, problém: abychom zajistili alespoň minimální předpoklady pro práci, musíme věnovat neúměrnou část času na shánění, čekání, improvizování a práci s nedokonalým zařízením. Netroufám si tvrdit, kolik procent drahocenného času tak ztrácíme. Mluvím o této problematice také proto, že obecně platí jakési tabu o ní hovořit, místo toho se tvrdí, že vědeckovýzkumná základna je procentuálně rovna vědeckovýzkumným základnám předních průmyslově vyspělých zemí. To je ovšem obrovský sebeklam, ze kterého se musíme velmi rychle dostat. Za současného stavu není naše vědeckovýzkumná základna schopna výrazněji přispět k zvládnutí vědeckotechnického pokroku a jeho využití v naší průmyslové výrobě. Mohu Vás ubezpečit, že máme kupř. stále větší problém s návrhy na státní ceny. To také něco signalizuje.

Ale vraťme se k problému výchovy tvůrčích pracovníků na vysokých školách. Řekl jsem, že předpokladem výchovy tvůrčích pracovníků je tvůrčí vědecká práce, která se rozvíjí okolo vědeckých osobností, které vytvářejí vědecké školy. Existují u nás i za předpokladu, že se v singulárních případech vytvoří předpoklady materiálně technického charakteru, možnosti vzniku vědeckých škol? Zdá se, že jsme svědky takových skutečností stále řidčeji. V čem to vězí, v nedostatku talentovanosti nás Čechů a Slováků, v nedostatku erudice? Domnívám se, že tady významně zasáhla i byrokracie, která prostoupila celý náš život, přičemž si nejsem jist, zda jsme tomu nepřispěli třeba jenom tím, že se smířlivě přizpůsobujeme i tam, kde víme, o co jde. Zvykli jsme si kupř. na kolektivní rozhodování a projednávání, svoláváme velké kolektivy na řešení nepodstatných problémů. A tak vysedáváme na jednáních, ke kterým nemusíme nic říct, a ani to nikdo od nás nechce. Chcete markantní příklad? Obhajoby kandidátských prací. Jejich průběh Vám nemusím popisovat. A přitom v jiných zemích je dostatečný počet členů komise tři, přičemž nebezpečí nízké náročnosti je podstatně menší, a komise se nesjíždí z celé země. Všechno je jaksi u nás organizováno tak, aby se údajně dosáhlo maximální objektivity, ve skutečnosti je tomu naopak. Přičemž nelze současně vyloučit u každého z nás jakýsi pocit apriorního podezírání z neseriózního jednání, přičemž mimo oblast kontroly se samozřejmě dostává to nejpodstatnější, naše vlastní odborná činnost. Tady se jaksi automaticky naše serióznost předpokládá. Každý z nás ví, jak nás dovedou přivést z míry různé úkoly spojené s nikomu nepotřebným výkaznictvím nejrůznějšího druhu. Suma sumárum se skládá pracovní den každého z nás z prací, které mají velmi nepříznivý vliv na naši vlastní produktivní činnost v míře, která nemůže být považována za únosnou. Všechny tyto nepříznivé vlivy mají bezesporu vážný vliv na tvůrčí atmosféru, na pracovní pohodu, přičemž jsme si zvykli i tyto snadno odstranitelné překážky považovat málem za objektivně nutné.

Nezdá se Vám, že těch problémů s vytvořením podmínek potřebných pro výchovu tvůrčích pracovníků je příliš mnoho? Mně samému se to rovněž zdá. Myslím si, že je proto třeba zahájit vážnou kampaň především v tisku, abychom na tyto problémy upozornili, současně přitom dali náměty na řešení.

Dovolte mi, abych pokračoval v rozboru dalších problémů, které přípravu tvůrčích pracovníků provázejí. Domnívám se, že je to společenské postavení tvůrčí inteligence, které stále nezaujímá to místo v žebříčku společenské významnosti, které mu patří. Naopak, velmi často je postavení tvůrčích pracovníků zlehčováno, málem jsou stavěni do jedné řady s nepotřebnou administrativou, neberou se ohledy na jejich specifické potřeby, kupř. ty tahanice okolo tzv. volné pracovní doby. S podivením jsem poslouchal v televizní relaci reakci představitele vyššího odborového orgánu na vývody ředitele určitého výzkumného ústavu, který zavedl volnou pracovní dobu tvůrčích pracovníků jako mimořádně efektivní prostředek pracovní iniciativy. Zavedení volné pracovní doby pro kohokoliv je protiprávní a může být postihováno i vysokými pokutami. Ale odborové orgány jsou prý si vědomy významu volné pracovní doby a její legalizování se připravuje.

Společenské postavení tvůrčích pracovníků není v průmyslu nijak výjimečné, spíše bych řekl, že se setkávají s tolika problémy a překážkami, že je téměř nad jejich síly prosadit se, a v současné situaci v průmyslu nutně rezignují. Náš průmysl obecně nepovažuje výsledky vědy za základ a podmínku zásadních inovací. Místo toho se dal na cestu kopírování s velkým časovým zpožděním. Pravda, v některých oborech nemáme jinou šanci, ale i pro kopírování potřebujeme mimořádně erudované a talentované pracovníky s potřebnými návyky a zkušenostmi z experimentální práce v dobře zařízených laboratořích. To všechno je nezbytný předpoklad, chceme-li změnit nepříznivou situaci v našem průmyslu, který ve všech významných oborech zaostal, přičemž se odstup od světového vývoje nadále zřetelně zvětšuje. Nevidím jinou možnost, než výrazné zlepšení přípravy tvůrčích pracovníků a vytvoření takových podmínek v realizační sféře, aby se mohli prosadit. Nebude to snadná záležitost. Mám až příliš mnoho negativních poznatků. Náš průmysl dovede totiž zabít mnoho dobrých výsledků opatrnictvím, laxním přístupem k jejich zavedení, nedbalou a pomalou prací, neschopností zorganizovat všechny potřebné činnosti spojené 8 úspěšnou realizací námětu a jeho prosazení do využití. Navštívil jsem v Tokiu továrnu firmy Jeol na výrobu elektronových mikroskopů, spektrometrů NMR a hmotnostních spektrometrů, která se zabývá samozřejmě také výzkumem a vývojem, a je tzv. assembling factory. Tisíc pracovníků smontuje a prodá 1000 elektronových mikroskopů ročně! (Tesla Brno mimochodem stěží 50 zhruba se stejným počtem pracovníků.) S určitým pocitem rozladění jsem si prohlédl rastrovací elektronový mikroskop s možností spektroskopie Augerových elektronů, který je novinkou, přičemž je použito zřetelně některých řešení z našeho mikroskopu BS 350, který byl realizován před více než deseti lety a který je namísto dalšího rozvoje Teslou soustavně zatracován.

Jestliže do výroby nepošleme co nejvíce tvůrčích pracovníků vědomých si svých kvalit, své převahy v erudici odborné, v organizačních schopnostech, ve vytrvalosti překonávat a řešit problémy, nemůžeme čekat výraznější obrat. Současná praxe není schopna ze svých sil žádného zvratu. Opatrnictví, snaha o bezkonfliktnost, nedostatečné znalosti a schopnosti vedoucí k potlačování všeho progresivního jsou charakteristické pro řadu „neklasických“ oborů.

Jistě mi dáte za pravdu, že současná situace po mnoha stránkách není taková, aby bylo možné jen, jak jsem v úvodu zdůraznil, proklamacemi dosáhnout výrazné změny. Mladý člověk je velmi kritický ke všemu v okolí. Chceme-li vytvořit „atmosféru nesmiřitelnosti s nezájmem, nedisciplinovaností a průměrností“, musíme dosáhnout toho, aby studenti především na konkrétním stavu úrovně odborné vědecké práce a možnostech pro ni na katedrách poznali, že jsou v kolektivech skutečně nejvíce erudovaných, předních vědců a odborníků, kteří představují špičku ve státě, která je respektována a uznávaná. Pro dosažení tohoto stavu musíme velmi mnoho udělat sami, velmi mnoho však musí do řešení tohoto, podle mého názoru v současné době nejnaléhavějšího úkolu, vložit společnost. Domnívám se, že dokonce výrazně na úkor prostředků vkládaných do modernizace průmyslové sféry, jak jsem již uvedl.

Dovolte mi závěrem stručně zrekapitulovat podmínky, které je nutné bezpodmínečně splnit, máme-li dosáhnout potřebného obratu v přípravě tvůrčích pracovníků na vysokých školách a jejich uplatnění v průmyslové praxi:

1. Je to především výrazné zvýšení náročnosti na úroveň vědeckovýzkumné činnosti pracovníků vysokých škol. Vědeckovýzkumná činnost musí být hodnocena především a musí snést kritéria světovosti. Budete se možná ptát, kdo má tuto činnost hodnotit? No přece profesor, který pracoviště vede. Na tom místě by neměl být přece nikdo jiný než známý a uznávaný vědec.

2. Je to dále potřebné materiální a přístrojové zabezpečení na odpovídající světové úrovni, přičemž se tady míní vybavení, jaké mají univerzity středně ekonomicky silných států, kupř. západní Evropy, které musí být naším vzorem. Za neoddělitelnou část materiálního zabezpečení je třeba považovat výstavbu ať už naplánovaných nebo nenaplánovaných, ale mimořádně potřebných areálů, poskytujících vyhovující prostorové podmínky. Pro splnění tohoto bezpodmínečného úkolu revidovat národohospodářské plány a přesunout prostředky z oblasti průmyslu do oblasti školství.

3. A konečně je to vytvoření takového klimatu ve společenské praxi, aby potřeba tvůrčích pracovníků se stala do té míry naléhavou, aby se tvůrčí pracovníci nemuseli prosazovat proti všem, ale aby naopak u všech nalézali bezpodmínečnou podporu. Víte sami dobře, že nemám na mysli žádné elitářské zásady, ale bez politické podpory, která musí spočívat v jednoznačném dodržování už vyhlášené zásady, že na prvém místě musí být u každého vedoucího pracovníka splněny odborné předpoklady, přičemž politické jsou samozřejmé, nemůže se prosadit žádný tvůrčí pracovník. Praxe má bezpočet příkladů.

Dosáhnout výrazné změny v realizaci podmínek pro přípravu tvůrčích pracovníků, bez nichž žádná společnost nemůže existovat a rozvíjet se, nebude snadné. Ale bude to bezpodmínečně nutné. Je třeba litovat, že opět jako už častokrát stojí před námi realizace procesu, která je mnohem náročnější z hlediska vynaloženého úsilí a energie, než kdyby bylo použito postupné evoluce. Připočtěme to tedy k chybám, které doprovázejí každý experiment, a považujme dosavadní postup za nezdařený, ale nutný experiment.

Je samozřejmé, že by mě zajímaly Vaše názory, především nesouhlasné.

HMOTNOST A ENERGIE PŘED EINSTEINEM A PO NĚM

Jiří Bičák

Katedra matematické fyziky MFF UK 180 00 Fraha 8, V Holešovičkách 2

Příspěvek podává stručný přehled historického vývoje pojmů hmotnost a energie v předrelativistické fyzice a rozebírá změny v chápání těchto pojmů po vytvoření teorie relativity. Krátce se dotýká i některých současných otázek. V této písemné verzi je podrobněji rozvedena historické část, v přednášce bylo více pozornosti věnováno novějším problémům.

1. Quantitas materiae

Historicky se fyzikální pojem hmotnosti vytvořil na základě pojetí setrvačné hmotnosti, které rozpracovali Kepler a Newton. Protože však jejich přístup vnitřně souvisel s předklasickým pojetím hmotnosti jako „množství (quantitas) materie“ a protože předklasické pojetí bylo po velmi dlouhé období součástí „fyzikálního“ obrazu světa a někdy vede k mylným interpretacím dodnes, zahrneme ho také do našeho rozboru.

Středověká filozofie chápala hmotu jako množství látky v tělese obsažené. Jde o první vyjádření kvantitativního aspektu hmoty – hmotě lze přiřadit číslo. Velmi blízko k pojmu quantitas materiae byl však už např. Iacretiue: „Nic nemůže být vytvořeno z ničeho. Příroda rozloží všechno na atomy, ale žádná věc nemůže být redukována na nic.“ (0 podstatě věcí.) Atomy mají váhu (dříve považovanou za náhodnou vlastnost stejně jako barva a pach), která se stává podstatným atributem materie. Z Lucretiových formulací lze vyčíst i zákon zachování hmoty. Nebo Lucianovo líčení moudrosti Demonaxovy: „Někdo se ptal Demonaxe: Spálím-li sto liber vlny, kolik dostanu liber kouře? ... Zvaž popel, zbytek je všechno kouř.“ Tyto myšlenky však byly ojedinělé, obecně vzato starověk hmotu za množství materie nepovažoval.

Formování pojmu „množství materie“ ve středověku je vnitřně spjato s některými teologickými a scholastickými problémy jako např. stvoření, smrt, transsubstanciace. Tyto problémy odpovídaly filozofickým pojmům vzniku, anihilace a transmutace materie, a souvisely tedy také s principem zachování hmoty v jeho počáteční metafyzické formě. Například transsubstanciaci nacházíme v biblickém stvoření Evy z žebra Adamova. Princip zachování hmoty v souvislosti s touto transsubstanciací přinášel další problém – zda bylo možno stvořit Evu z žebra Adamova bez dodání další materie. Podobně úvahy o přeměně chleba a vína v tělo a krev Krista se chápaly mnohem „materialističtěji“ než dnes a vedly ke snahám o vyjádření „množství materie“.

V současném myšlení je hmotnost ve smyslu „množství materie“ v nejlepším případě pojmem metafyzickým v protikladu k čistě vědeckému pojetí. Proč je z nynějšího hlediska kvantitativní určení „množství materie“ nemožné? Materie jako taková je z fyzikálního hlediska nepostižitelná a nepochopitelná, je neměřitelná. Množství materie v tělese nelze vyjadřovat ani počtem částic, z nichž se těleso skládá, nebot neexistuje žádná jediná fundamentální částice. Kdyby nějaká základní elementární částice existovala – říkejme jí třeba „hmoton“ – taková, že by se všechny dnes známé elementární částice z ní skládaly a pomocí níž by bylo možno charakterizovat také fyzikální pole (tedy i částice zprostředkovávající interakci jako např. fotony), pak by o hmotnosti jako „množství materie“ hovořit šlo. Totiž: stůl by obsahoval třeba 10⁹⁸ „hmotonů“, židle 10⁹⁷ „hmotonů“ atd. – hmotnost by se udávala v množství „hmotonů“. Dnes však známe několik druhů kvarků, různé leptony a částice, které zprostředkovávají mezi nimi čtyři typy interakcí.

Jedině vlastnosti hmoty lze měřit. Jestliže ovšem definujeme velikost hmotnosti pomocí velikosti jedné z měřitelných vlastností hmoty, pak hmotnost samozřejmě závisí na tom, která vlastnost byla vybrána jako kritérium. V klasické (newtonovské) fyzice například zcela náhodně vychází, že dvě různé vlastnosti hmoty – setrvačnost v klidu nebo v pohybu a gravitační přitažlivost hmoty vedou k jednomu a témuž kvantitativnímu ohodnocení (setrvačné hmotnost = gravitační hmotnost). Jestliže by se ale jako kritérium vzala setrvačnost a třeba tepelná kapacita těles, pak by z obou veličin vycházely zcela různé číselné výsledky pro velikost hmotnosti.

2. Setrvačná hmotnost

Všeobecně se přijímá, že hmotnost ve smyslu hmotnosti setrvačné byla zavedena až Newtonem. Ve skutečnosti tento pojem byl výsledkem postupného vývoje, který začal od Johannese Keplera a byl završen Leonhardem Eulerem. Ještě Galilei vypočítává jako hlavní vlastnosti hmoty tvar, lokalizaci, pohyb, atd. – tedy vlastnosti geometrické nebo kinematické. Z počátku se tu nevyskytuje žádný poukaz na nějaký dynamický aspekt hmoty. Ovšem v Galileiho „Dialogu“ je již naznačena myšlenka inerciální hmotnosti. Salviati se ptá: „Neexistuje vnitřní přírodní kvalita, která klade odpor pohybu?“ ... Galileiho fyzika však přesnou formulaci pojmu hmotnosti nevytvořila a ani nepřišla na to, že je nutno tento pojem jako základní pojem připojit k již existujícím pojmům délky (prostoru) a času. Až keplerovská astronomie zaplnila tuto mezeru, a tím připravila předpoklady k tomu, aby Newton mohl vybudovat základní soustavu veličin klasické mechaniky.

Kepler vycházel ze síly jako základního pojmu, když zkoumal závislost rychlosti planety na vzdálenosti od Slunce. Ale i hmotnost hrála u něho principiální roli. Kepler ji sice chápal stále jako „množství materie“, jako prvý však jí přisuzoval schopnost odporovat pohybu. Pojem síly rozvíjel Kepler z pojmu aktivity „ducha“ nebo „čisté formy“, pojem hmotnosti z pojmu „materie“. Tradiční protiklad formy a materie byl základem. Kepler objevil, že faktor, který působí proti aktivní síle, se musí nacházet v samotné materii, neboť v souhlase s novoplatonickou tradicí je „charakter materie zejména takový, že materie projevuje odpor proti uskutečnění formy“.

Kepler odvozuje materiální charakter planet z jejich vnitřní schopnosti odporovat pohybu: „Jestliže by materie nebeských těles neměla vlastnost inercie (odporu k pohybu), podobnou váze těles, pak by nebylo třeba téměř žádné síly k tomu, aby se tělesa uvedla v pohyb; nepatrná síla by stačila k tomu, aby jim udělila nekonečnou rychlost. Protože však periody planetárních oběhů jsou konečné (některé planety mají kratší periody, jiné delší), je zřejmé, že materie musí mít vlastnost inercie, která tyto rozdíly vysvětluje. ... při pohybu planet dochází k boji mezi přemisťující silou Slunce a materiální inercií planet.“ Inercie je tedy nejen neschopnost planet k přemístění sána sebe z jednoho místa na druhé, ale má i aktivní aspekt – odporuje zvnějška udělovanému pohybu. Tento odpor k pohybu je u Keplera v přímé souvislosti s „množstvím materie“: „inercie, neboli odpor proti pohybu, je pro hmotu charakteristická a je tím větší, čím více je materie v daném objemu.“

Tím je dáno do souvislosti pojetí „množství materie“ scholastiků a Keplerův nový pojem inercie. Existuje tu možnost interpretovat výraz „množství materie“ jako veličinu úměrnou inercii materie (v naší terminologii jako setrvačnou hmotnost).

Kepler tedy jako první vyslovil myšlenku inercie. Nutno ovšem připomenout, že chápal inercii jen jako nemožnost spontánního pohybu nebo odpor proti přechodu z klidu do pohybu. Význam inercie jako snahy po pokračování v pohybu (setrvačnost v pohybu) už tělesu udělenému (který takto poprvé vyslovil Descartes) Kepler neznal. Keplerově inercii bychom samozřejmě mohli přisoudit obecný význam, jestliže bychom klid i pohyb považovali za fyzikálně identické stavy, popsané vzhledem k různým vztažným systémům. Kepler byl takovému výkladu ovšem velmi vzdálen.

Přesto je Keplerův podíl na vývoji pojmu inerciální hmotnosti obrovský, uvážíme-li zvláště, že scholastická schémata považovala síly odporu proti pohybu za duchovní, volní síly, nemající vztah k fyzikálním přírodním zákonům (viz například názor, že pohyb planet se děje díky andělům, kteří je „tlačí“ po pozorovaných drahách).

Keplerově koncepce inerciálního chování hmoty a závěry získané z experimentů a teorie srážek těles (o nich se ještě zmíníme při diskusi zákona zachování hybnosti a energie) byly sjednoceny v díle Newtonově. Newton píše v Principiích stále ještě o substanciální (látkové) hmotě: „Množství materie' je míra hmotnosti, která je úměrné hustotě a objemu ... například vzduchu dvojnásobné hustoty je ve dvojnásobném objemu čtyřnásobné množství.“ Tato definice hmotnosti pomocí hustoty není explicite obsažena ve třech základních Newtonových zákonech – historikové soudí, že byla zavedena pod vlivem Boyleových pokusů se stlačováním plynů (v nichž hustota hraje důležitou roli). Dříve než budeme Newtonovu definici posuzovat, uveďme, že Newton rovněž zavádí pojem „vrozené síly“ (vis insita) jako schopnost odporu, v důsledku níž „každé těleso ponecháno samo sobě setrvává ve svém stavu – ať je v klidu nebo v rovnoměrném pohybu“. Newton tuto schopnost (sílu) nazývá inercii. Inercie je jakási „spící“ síla, která se projeví pouze tehdy, jestliže jiná (vložená) síla mění pohybový stav tělesa.

Newtonova definice hmotnosti byla často kritizována především proto, že Newton nedefinoval hustotu, a jeho definice má proto charakter logického kruhu. Paul Volkmann: „Newton řekl: 'Nedefinuji čas, prostor, místo, pohyb, protože jsou všem velmi dobře známy' ... mil také prohlásit: 'Nedefinuji hmotnost'.“ Ernst Mach ve své Mechanice nazývá Newtonovu definici „nešťastnou“ nejen pro logický kruh v definici, ale především namítá proti užívání termínu „množství materie“, které podle něho nemá žádný fyzikální smysl.

Je třeba mít na paměti, že v Newtonově koncepci hmoty dominují dva primární nezávislé pojmy – množství materie a inercie. Newton v třetí knize Principií zavádí univerzální vlastnosti těles (např. rozprostraněnost, pohyblivost, ...). „Takové vlastnosti, které nemohou být zesíleny Si zeslabeny a které mají všechna tělesa, u nichž se lze o tom přesvědčit, je třeba považovat za vlastnosti všech těles všeobecně.“ Mezi tyto vlastnosti patří též inercie (ne už tíže – váha, která závisí na výšce nad Zemí). Různá tělesa podle Newtona vykazují různou inercii, inercie je ovšem pro dané těleso stálá. Klasická „newtonovská“ mechanika pak nazývá tuto neměnnou veličinu, které na ničem nezávisí a na které závisejí ostatní veličiny, inerciální (setrvačnou) hmotností tělesa. Ale Newton sám jen postuloval úměrnost mezi inercii a druhou fundamentální charakteristikou daného tělesa – „množstvím materie“.

Pravděpodobně nejužívanějším způsobem zavedení setrvačné hmotnosti v současné klasické fyzice je Maxwellova definice hmotnosti jako podílu síly a zrychlení, uvedená v jeho knize „Hmota a pohyb“. Maxwell vychází z předpokladu, že je možné zařídit, aby velikost síly, kterou určité těleso působí na jiné tělesa, byla v různých situacích stejná. Hmotnosti dvou těles jsou sobě rovné, když spirála stlačené na určitou délku jim udělí za daný čas stejné zrychlení. Uvažujeme-li dvě různá tělesa, pak změřením jejich zrychlení a₁, a₂, která jsou vyvolána stejně stlačenou spirálou, definujeme m₂ = (a₁/a₂) m₁. Zvolíme-li m₁ = 1, určíme m₂.

Maxwellova definice hmotnosti je založena na definici síly prostřednictvím 2. Newtonova zákona. Ačkoliv je newtonovská mechanika jednou z nejjednodušších fyzikálních teorií, neumožňuje vytvořit explicitní definice základních pojmů, které obsahuje. Whiteheadovu poznámku „získáváme znalosti o silách tím, že máme teorii o hmotách, a znalosti o hmotách z teorie o silách“ však dnes v žádném případě nechápeme jako kritiku teorie. Víme, že všechny fyzikální teorie obsahují základní zákony, které současně poskytují definici základních pojmů, které v nich vystupují, a umožňují dělat předpovědi. (Hovoří se o implicitní definici pojmů.) Uvědomujeme si, že ve fyzice nelze nejprve definovat pojmy a potom konstruovat zákony. Pojmy, způsoby měření, teorie a zákony vznikají a rozvíjejí se současně. Jedním experimentem (např. podle předchozí Maxwellovy definice) určíme m. Jinými experimenty určíme charakter (dosud neznámého) silového pole podle vztahu F = m a. Tím nalezneme silové pole jako funkci polohy: F = F(xⁱ). Druhý Newtonův zákon se pak stane opravdu pohybovou rovnicí_} m (d²xⁱ/dt²) = F(xⁱ). Řešením můžeme dělat předpovědi, xⁱ = x^l(t), a ty pak konfrontovat se skutečností.

3. Hybnost a energie

Nejjednodušší tvar zákona setrvačnosti (rychlost tělesa zůstává konstantní co do velikosti i směru, pokud na těleso nepůsobí vnější síla) se stal běžně přijímaným od dob Galileiových. Ještě před Newtonem se však vyšetřovala složitější situace – srážka dvou těles, byla považována za nejjednodušší příklad interakce. Srážka dvou těles umožňuje nejjednodušším způsobem vyložit zákony zachování hybnosti a energie v izolované soustavě dodnes a z teorie srážek budeme také vycházet při odvozeni výrazu pro relativistickou hmotnost. Již René Descartes vytvořil veličinu „množství pohybu“, rovnou součinu hmotnosti a rychlosti, m v, a na základě filozoficko-teologických úvah (jak uvádí von Laue) vyvozoval, že se součet „množství pohybu“ všech těles při srážce zachovává. Neuvědomoval si však vektorový charakter rychlosti.

V roce 1668 vypsala Royal Society soutěž na téma teorie srážek. (V té době bylo Newtonovi jen 26 let, Principia vyšla až téměř o 20 let později.) Dva z kandidátů byli Christian Huygens a Christopher Wren. (Až o 7 let později pokládal Wren základní kámen ke svému hlavnímu dílu – katedrále sv. Pavla v Londýně.) Huygens i Wren již užívali zákona zachování hybnosti ve správném tvaru a v případě dokonale pružných srážek si dokonce i uvědomovali, že se zachovává součet součinů hmotností a kvadrátů odpovídajících rychlostí těles, m v². Jde patrně o první (ač neuvědomělé) použití zákona zachování energie (v matematickém tvaru) ve fyzice. Huygens nadto vyšetřoval srážku i z hlediska plující lodi, a tak zřejmě jako první použil i klasický (Galileiho) princip relativity. (Principu relativity při studiu srážek budeme dále ještě užívat.)

Klasické mechanika jako fyzikální věda byla ovšem v principu dovršena Newtonem v Principiích. Kombinaci dvou základních zákonů, a to (1) časová změna hybnosti hmotného bodu rovna působící síle a (2) síly, kterými na sebe působí dva hmotné body, jsou stejně veliké a opačného směru, okamžitě odvodíme, že interakce mezi libovolným počtem hmotných bodů v daném systému nemůže změnit celkovou hybnost systému. Ta zůstává konstantní, pokud na systém nepůsobí vnější síly. (Uvažme, jak z hlediska speciální relativity prozíravě Newton formuloval pohybový zákon : , nikoliv , i když z , m = konst plyne druhá formulace. Pouze první tvar se však přenáší do speciální relativity, přičemž m se stává funkcí rychlosti.)

I když jako fyzikální problém byla klasická mechanika v podstatě uzavřena Newtonem, jako matematická teorie byla dále podivuhodně rozvíjena v dílech Bulera, Legrange, Hamiltona a dalších. Tyto elegantní nové formulace měly vliv i na konstrukci nových fyzikálních teorii, zvláště na kvantovou mechaniku a kvantovou teorii pole, a jsou velmi přesvědčivým důkazem toho, že matematické přeformulováni fyzikální teorie může významně pomoci při vytvářeni teorie nové. Protože však neměly bezprostřední vliv při budováni speciální a obecné relativity, nebudeme se jimi zabývat.

Třebaže už Huygens a Wren užívali při etudiu srážek součinu mv , až Gottfried Wilhelm Leibniz obrátil na tento výraz pozornost jako na základní fyzikální veličinu. Dal ji název „vis viva“ (živá sila), který se udržel až do 19. století. Gustave Gaspard Coriolis zavedl poloviční veličinu a Johannes Bernoulli ji označil jako „energii“. Dnes místo„vis viva“ říkáme kinetická energie, „energie“ má pro nás obecnější význam. Bernoulli ovšem už věděl, že v uzavřeném mechanickém systému pokles kinetické energie neznamená snížení „akceschopnosti“ systému. Jean Victor Poncelet začátkem 19. století jako první zavedl „práci“ jako součin síly a dráhy, která je v mechanice rovna změně energie. (Již v roce 1773 se pařížská akademie rozhodla, že nebude přijímat další návrhy perpetua mobile, protože už ztratila příliS mnoho času zkoumáním navrhovaných schémat.)

Koncem 18. století vcházelo do obecného povědomí, že existují procesy, při nichž kinetická energie se snižuje, ale roste teplota těles, která se procesu zúčastní. První tepelné stroje se pojí se jmény Sadi Carnot a Bénoit Clapeyron. Přišel tak čas, kdy se zákon zachováni mechanické energie začal zobecňovat na univerzálně platný zákon zachování energie v různých formách.

Max Planck přisuzuje myšlenku univerzálně platného zákona zachování energie lékaři Juliusu Robertu Mayerovi, který v roce 1842 vyslovil věty typu „z ničeho nemůže něco vzniknout“, „nic nevede k ničemu“ (v tomto případě je snad i česky správnější „nic vede k ničemu“). Mayer měl k zákonu zachování energie spíše obecný filozofický přístup. Nechal na jiných, aby jej odvodili na základě detailních experimentů, jako první však správně určil mechanický ekvivalent tepla. James Joule v roce 1843 napsal článek o tepelných a chemických účincích elektrického proudu a brzy poté také určil mechanický ekvivalent tepla, přičemž uvažoval změny mechanické práce na teplo buď přímo nebo elektricky nebo stlačováním plynů.

Princip zachování různých forem energie však v obecnější míře především rozvinul začátkem padesátých let minulého století Hermann von Helmholtz. Zavedl pojem potenciální energie, energie statického elektrického a magnetického pole, rozebíral problém produkce energie při vzniku elektrického proudu v galvanickém článku, atd. Max von Laue zdůrazňuje, že Helmholtzových metod např. užíváme, když počítáme energii gravitačního (resp. elektrostatického) pole jako součin hmotností (resp. nábojů) a potenciálů, při vztahu energie „uložené v poli“ a interakční energie mezi jednotlivými objekty budícími pole. Max von Laue uvádí, že ovšem Helmholtzovy úvahy nebyly nejprve snadno přijímány, protože vědci se obávali, že vzniká něco podobného jako Hegelova „přírodní filozofie“, proti níž museli dlouho bojovat. Kolem roku 1860 byl však zákon zachování energie izolovaných systémů všeobecně uznán.

Rozpracováni Maxwellovy teorie elektromagnetického pole vedlo po roce 1873 k pojmům toku energie (Poyntingův vektor), zákon zachování hybnosti byl formulován i pro elektromagnetické pole, speciálně i pro pole záření. Aby se naše poznámky nerozrostly nad přijatelné meze, nebudeme zde tyto pojmy ani jejich historii rozebírat (několik příkladů bylo diskutováno na přednášce). Dodejme jen, že v teorii elektromagnetického pole se začátkem našeho století začaly objevovat výsledky naznačující, že hmotnost pohybujícího se objektu závisí na jeho rychlosti a souvisí také s energií v objektu obsažené. Z matematického, ale především z fyzikálního hlediska jasné vztahy tohoto typu však přinesla až speciální relativita. K té se nyní obrátíme. Přestaneme sledovat historickou nit. Budeme mít na zřeteli jen hlavní myšlenky a co nejjednodušší způsob odvození těchto vztahů – takový, který pochopí student gymnázia bez znalosti infinitezimálního počtu.

4. Hmotnost a energie ve speciální teorii relativity

Nemůžeme zde podrobně rozebírat základní myšlenky vedoucí ke speciální relativitě. Naším bezprostředním cílem bude především důkaz tvrzení, že setrvačná hmotnost částice závisí na rychlosti částice, a naznačíme také, jakým způsobem lze tuto závislost zjistit. Existují dva způsoby odvození, oba vedou k témuž výsledku. Původní Einsteinův, jenž je již obsažen v jeho prvním článku o speciální relativitě. Je založen na rozboru pohybu nabité částice v elektrickém poli. Lse ukázat , že rovnice pohybu elektronu vyhovují speciálnímu principu relativity (tj. mají stejný tvar ve všech inerciálních systémech), závisí-li hmotnost určitým způsobem na rychlosti. Někteří fyzikové ovšem cítili nedostatek v tom, že se odvozuje základní zákon mechaniky ze zákonů elektrodynamiky (bylo třeba užít výrazu pro elektrickou sílu působící na nabitou částici), a vznikla proto přirozená snaha odvodit závislost hmotnosti na rychlosti pouze na základě úvah mechaniky a pokud možno obejít pojem síly. K tomu se nejlépe hodila teorie srážek. Na základě této teorie Lewis a Tolman ukázali, že setrvačná hmotnost musí nutně záviset na rychlosti, pokud platí v teorii srážek princip relativity a Lorentzova transformace.

Jak známo již z klasické mechaniky, existují dva základní typy srážek dvou těles – srážka (dokonale) nepružná, při níž se srážkou vytvoří pouze jedno těleso, a srážka (dokonale) pružné, po níž se individuálně pohybují opět dvě tělesa. V obou případech jde o izolovanou soustavu dvou těles, na která nepůsobí vnější síly, a proto v obou případech platí zákon zachování hybnosti (uvažujme jen jednu dimenzi)

m₁ u₁ + m₂ u₂ = ( m₁ + m₂) ū

v případě nepružné srážky, zatímco při pružné srážce

m₁ u₁ + m₂ u₂ = m₁ ū₁ + m₂ ū₂

(veličiny bez pruhu označují rychlosti těles před srážkou, pruhované veličiny – po srážce; m₁, m₂ jsou hmotnosti jednotlivých těles). Rozdíl mezi srážkou nepružnou a pružnou je jak známo v tom, že v případě nepružných srážek se nezachovává mechanická energie.

Abychom co nejjednodušším způsobem nalezli vzorec pro setrvačnou hmotnost relativistické částice, omezíme se na speciální případ nepružné srážky: vyšetříme nepružnou srážku dvou stejných koulí se stejnou setrvačnou hmotností m . Především dokážeme platnost následující věty: Jestliže platí zákon zachování hybnosti v každém inerciálním systému ve stejném tvaru a jestliže platí relativistická věta o skládání rychlostí (která je bezprostředním důsledkem Lorentzovy transformace – tedy důsledkem postulátů speciální relativity), pak setrvačná hmotnost musí nutně záviset na rychlosti. Důkaz provedeme sporem. Předpokládejme, že hmotnost m každé z koulí nezávisí na rychlosti. Nechť v nějakém systému I´ probíhá nepružná srážka „symetricky“, takže u₁´ = u´ , u₂´ = − u´, ū₁ = ū₂ = 0. V systému I , který se vůči I´ pohybuje rychlostí − v , pak v důsledku adičního teorému rychlostí dostaneme

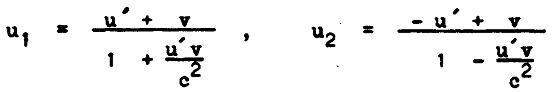
a pro rychlost po srážce samozřejmě ū₁ = ū₂ = v . Ze zákona zachování hybnosti v systému I, m u₁ + m u₂ = 2 m v , pak plyne

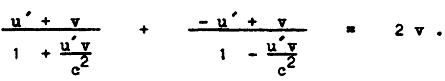
Rychlost u´ však můžeme předepsat libovolně, např. u´ = v , takže pak dostaneme

což je spor.

Nabízejí se tedy dvě možnosti: Buď připustíme, že platí zákon zachování hybnosti ve stejném tvaru jako v klasické fyzice (jak jsme výše předpokládali), a musíme se pak smířit s tím, že hmotnost závisí na rychlosti, nebo se pokusíme udržet hmotnost konstantní, ale zřekneme se zákona zachování hybnosti. První možnost je mnohem vhodnější. Zákony zachování hybnosti a energie jsou obecné zákony vlastní každé fyzikální teorii. Jsou to také jedny z nejjednodušších přírodních zákonů, protože říkají, že nějaká veličina je stále rovna konstantě. Již z tohoto hlediska bychom se v nové mechanice zákona zachování hybnosti neradi zříkali. Nadto uvažme, že každé těleso má svoji strukturu, skládá se z mnoha částic, které na sebe navzájem působí, v důsledku zákona zachování hybnosti však těžiště tělesa zůstává v klidu (nebo v rovnoměrném přímočarém pohybu), nepůsobí-li na těleso vnější síla. Kdyby neplatil zákon zachování hybnosti, a tedy ani zákon o pohybu těžiště, mohlo by se těleso samo od sebe v důsledku vnitřních sil uvést do pohybu.

Předpokládejme tedy, že zákon zachování hybnosti platí a že hmotnost je obecně nějakou funkcí rychlosti m(u). A vraťme se k jednoduchému příkladu nepružné srážky. Mějme dvě stejné koule a v nějakém inerciálním systému I nechť „levá“ koule se pohybuje rychlostí u „zleva doprava“, „pravá“ koule nechť před srážkou stojí. Výsledné těleso po srážce nechť se pohybuje zleva doprava rychlostí ū. Zákon zachování hybnosti pak má v I tvar

m(u) u  = M(ū) ū , (1)

kde M je hmotnost tělesa vzniklého srážkou. Abychom nalezli vztah mezi u a ū , vyšetříme tutéž srážku z hlediska systému I´, který se vzhledem k I pohybuje rychlostí u zleva doprava. V tomto novém systému je zřejmě levá koule v klidu, pravá se pohybuje rychlostí −u . Cely obraz srážky je v systému I´ symetrický k obrazu v systému I, jen levá a pravá koule se prohodily. Je proto zřejmé, že v soustavě I´ se výsledný produkt srážky pohybuje rychlostí −ū . Použijeme-li nyní adičního teorému rychlostí pro výsledný produkt srážky, dostaneme vztah mezi u a ū ve tvaru

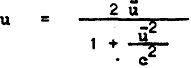. (2)

Konečně užijeme další vztah, který vyjadřuje zákon zachování hmotnosti během srážky:

m(u) + m(0) = M(ū) . (3)

Tento vztah můžeme snadno dokázat, když celou srážku vyšetřujeme v nějakém dalším systému I´´, který se vzhledem k I´ pohybuje nějakou rychlostí podél osy y (např. „zezdola nahoru“), a předpokládáme, že i v tomto systému platí zákon zachování hybnosti a že (samozřejmě) platí adiční teorém pro skládání rychlostí v relativistickém tvaru. Srovnáním (1), (2), (3) pak snadno jednoduchými úpravami dojdeme ke známému relativistickému vzorci

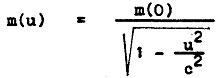. (4)

Tak z platnosti zákona zachování hybnosti ve všech inerciálních systémech dospějeme ke vztahu, který určuje, jakým způsobem hmotnost závisí na rychlosti. Hmotnost m(0) se běžně označuje jako m₀ a nazývá se klidová hmotnost; je to hmotnost měřená v systému, v němž těleso je v klidu. V systému, v němž se pohybuje rychlostí u, je hmotnost téhož tělesa dána vztahem (4). Znamená snad (4), že i ve vakuu existuje nějaká látka, která se při pohybu tělesa na těleso „nalepuje“, a tím zvyšuje množství látky v tělese obsažené? Samozřejmě nikoliv. Hmotnost, o níž hovoříme, je setrvačná hmotnost, která charakterizuje odpor tělesa vůči urychlování a nemá nic společného s historickou „quantitas materiae“. Skutečnost, že setrvačná hmotnost závisí na rychlosti, neříká nic jiného než to, že tělesa (částice) pohybující se s velkou rychlostí kladou mnohem větší odpor urychlování než tělesa, které se pohybují rychlostí malou. Je snazší urychlit raketu z rychlosti 200 000 km/s na 200 001 km/s , třebaže v obou případech se rychlost mění stejně, o 1 km/s . Vzorec (4) byl bezprostředně ověřen obrovským množstvím fyzikálních experimentů, musí s ním počítat konstruktéři urychlovačů elementárních částic. (Např. hmotnost elektronů se v urychlovačích může zvýšit více než 2 000×, takže elektrony pak mají větší hmotnost než protony v klidu.)

Patrně nejznámějším a díky popularitě speciální teorie relativity i nejotřelejším vzorcem je vztah setrvačné hmotnosti a energie. V klasické fyzice nemohla vzniknout otázka, zdali mezi setrvačnou hmotností a energií existuje nějaká souvislost. Setrvačná hmotnost nezávisela na hmotnosti, zatímco kinetická energie na ní zjevně závisela. Protože však ve speciální relativitě setrvačná hmotnost je dána vzorcem (4), otázka souvislosti mezi hmotností a energií nabývá na významu. Pro částici s hmotností m , která se pohybuje rychlostí v « c , můžeme psát

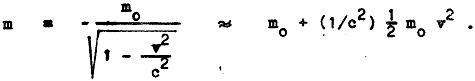
Tím, že tělesu, které je v klidu, udělíme jistou rychlost v , zvýšíme tedy jeho setrvačnou hmotnost o (1/c²) ½ m₀ v²  a zároveň mu dodáme kinetickou energii ½ m₀ v² . Tedy přírůstek kinetické energie ΔE = ½ m₀ v² a přírůstek setrvačné hmotnosti Δm = (1/c²) ½ m₀ v² spolu bezprostředně souvisejí: ΔE = c² Δm .

Vraťme se ještě k našemu příkladu srážky dvou nepružných koulí. Snadno zjistíme, že v systému, v němž těleso vzniklé srážkou je v klidu, platí

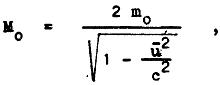
u  a  −ū jsou v tomto systému rychlosti koulí před srážkou. Výsledné těleso nemá klidovou hmotnost rovnu součtu klidových hmotností obou částic, ale M₀ je větší o součet kinetických energií obou koulí před srážkou, vydělený c² :

M₀ = 2 m₀ + 2 T / c² ,

kde T = ½ m₀ ū²  pro u « c . Když obě koule přejdou v uvažovaném systému do klidu, jejich kinetická energie se přemění na tepelnou (či elastickou): 2 T = Q . Proto M₀ = 2 m₀ + Q / c² . Tento vztah lze vyložit pouze tak, že přidáním tepelné energie Q (která vznikla přeměnou T ) se hmotnost zvětší o Q / c² . Opět můžeme psát Δm = ΔE / c² (v našem případě speciálně Δm₀ = ΔE / c² ).

Ve dvou konkrétních případech jsme viděli, že dodání energie ΔE vedlo ke změně hmotnosti Δm = ΔE / c² . Důkaz jsme provedli pouze v případě kinetické a tepelné energie, ve speciální relativitě však předpokládáme, že v případě libovolného druhu energie (elektrické, jaderné atd.) přidání energie ΔE vede k vzrůstu setrvačné hmotnosti o ΔE / c² . Einstein však s mimořádnou prozíravostí předpokládal více: nejenom přírůstky energie a hmotnosti jsou si úměrné, ale úměrné jsou i celková zásoba energie tělesa a jeho celková hmotnost:

E = m c² . (5)

Je-li těleso v klidu, pak klidové setrvačné hmotnosti m přísluší energie E = m c², přičemž tato energie zahrnuje všechny možné druhy energie. I v případě elektromagnetického pole zjistíme stejný vztah (nejjednodušeji ilustrovatelný v případě rovinné vlny). Energii žádného materiálního objektu nelze zvětšit, aniž bychom zároveň nezvětšili jeho setrvačnou hmotnost, a naopak, zvětšíme-li hmotnost objektu, zvětší se i jeho energie. Je-li jedna z veličin dána, je dána i druhá, protože c je univerzální konstanta. Z relativistického hlediska je zákon zachování (setrvačné) hmotnosti zároveň zákonem zachování energie. Vztah E = m c² bývá nazýván zákonem ekvivalence hmotnosti a energie.

Je třeba si však uvědomit, že obsahově jde o zcela odlišné pojmy: energie charakterizuje schopnost tělesa konat práci – má-li těleso velkou kinetickou energii, může konat práci, při níž vzniká energie jiné formy. Setrvačná hmotnost naproti tomu charakterizuje odpor tělesa vůči urychlování. Jde o dvě různé vlastnosti materie, které jsou spolu podle speciální relativity nerozlučně spjaty, číselně jsou si úměrné. V tomto smyslu jsou oba pojmy ekvivalentní. K obezřelosti při takových formulacích nás však nabádá antická anekdota. Byla navržena dvojí definice člověka: (1) člověk je tvor moudrý – homo sapiens; (2) člověk je dvojnožec bez peří. Dvě vlastnosti, které se nerozlučně projevují mezi všemi živočichy pouze u člověka. Až přišel vtipálek s oškubanou živou slepicí a prohlásil: „Ejhle člověk.“

S jiným příkladem dvou ekvivalentních pojmů, které charakterizují dvě zcela odlišné vlastnosti tělesa, se setkáváme v případě ekvivalence setrvačné hmotnosti a hmotnosti gravitační. Obě hmotnosti lze připsat každému tělesu, avšak každé z nich charakterizuje zcela jiné vlastnosti tělesa – odpor tělesa vůči urychlování a schopnost tělesa přitahovat se k jiným objektům.

Einstein nedošel ke vztahu mezi hmotností a energií snadno. Na podzim v roce 1905 v dopise Habichtovi o něm psal: „Je to zajímavý a fascinující sled myšlenek, ale nemohu vědět, zda se tomu milý Pánbůh nesměje a nevodí mě jen za nos.“ V přehledovém článku z roku 1910 poznamenává, že „v daném okamžiku není žádná naděje, že by se ekvivalence hmotnosti a energie mohla experimentálně ověřit“. Až v třicátých letech byl vztah E = m c² ověřován změřením jaderné vazbové energie a v roce 1937 byla z něho dokonce vypočítána rychlost světla na základě znalosti hmotností počátečních a konečných produktů v jaderných reakcích a energie, která při reakcích byla uvolněna. (Rychlost světla tak vyšla s přesností lepší než 0,5 %!)

Ani jaderná fyzika však přímo nedokazuje více než ΔE = Δm c² . Prozíravost a odvaha Einsteinova byla v postulování přímého vztahu E = m c² . Bylo velmi dobře možné (a s relativitou slučitelné), že elementární částice nelze destruovat. Pak by platilo pouze ΔE = Δm c² , protože např. nějaká složená částice s hmotností m by disponovala pouze energií (m − b) c² , kde b je součet klidových hmotností elementárních částic, které složenou částici vytvářejí. Při procesech s volným systémem těchto složených částic by se zachovávala celkové hmotnost ∑m c² , celkové klidová hmotnost ∑ b c² a veličina ∑ (m − b) c² . Jedině tuto poslední veličinu bychom však nazvali energií... Po pozorování anihilace páru elektron-pozitron (v roce 1933) bylo však zřejmé, že klidová hmotnost částic se může cele přeměnit na energii (setrvačnou hmotnost) záření.

Klidové energie makroskopických částic (těles) je obrovská: v každém gramu je obsaženo 9 ∙10¹³ joulů energie, což je zhruba energie prvních atomových bomb. Velmi malá část této energie je obsažena v tepelném pohybu molekul, z nichž je částice složena, a může být odvedena jako teplo. Další část je obsažena v mezimolekulárních a meziatomových vazbách a může být uvolněna např. při chemickém výbuchu. Další část je obsažena v excitovaných atomech a může být vyzářena. O něco větší část je obsažena v energii jaderných sil, kterými jsou k sobě vázány protony a neutrony v atomových jádrech; tato část může být uvolněna při jaderných reakcích. Zhruba 99 % klidové energie částice je však obsaženo v klidových hmotnostech jednotlivých elementárních částic, z nichž je makroskopická částice složena – především v klidových hmotnostech protonů a neutronů. Energii obsaženou v klidových hmotnostech lze ovšem uvolnit jen za velmi výjimečných podmínek, jako je tomu např. při zmíněné anihilaci párů elektron a pozitron. Podstatně větší část energie lze získat při procesech kolem černých děr.

Výše jsme ze zákona zachování hybnosti při nepružné srážce a z principu relativity elementárním způsobem odvodili závislost setrvačné hmotnosti na rychlosti a ekvivalenci hmotnosti a energie. V teorii srážek lze však také vyjít pouze z existence zákona zachování energie ve všech inerciálních systémech a odvodit zákon zachování hybnosti, závislost energie i hmotnosti na rychlosti a ekvivalenci hmotnosti a energie. Lze dokonce vyjít z takových axiomů teorie srážek, které obsahují jako parametr ε = c⁻² a v případě ε = 0 vedou ke klasickým výsledkům, pro ε ≠ 0 k relativistickým výsledkům. Tím se explicite vyjasní společná pojmová a formální struktura teorií srážek založených na newtonovské a einsteinovské kinematice. (Podrobnosti viz v článku J. Ehlerse „Relations between the Galilei-invariant and the Lorentz-invariant theories of collision“, ve sborníku „Space, Time, and Mechanics“, ed. D. Mayr, G. Süssmann, D. Reidel Publ. Co., Dodrecht 1983.)

5. Hmotnost a energie v obecné relativitě a v kosmologii – nedávné rozvoje a otevřené problémy

Tato široká a velmi živá tematika bude(?) v ústní verzi krátce charakterizována několika problémy: měřitelnost lokálního rozdělení energie a hybnosti materiálních objektů (částic a negravitačních polí) jako zdroje gravitačního pole prostřednictvím měření geometrie prostoročasu; princip ekvivalence a nemožnost lokalizace gravitační energie; celková energie a hybnost asymptoticky plochých prostoročasů reprezentujících izolované systémy, definovaná v „prostorovém“ a ve „světelném“ nekonečnu; nedávný důkaz pozitivní definitnosti celkové energie; vesmír jako dlouho trvající ( ΔT ≈ 15 ∙ 10⁹ let) kvantová fluktuace vakua – stvoření „ex nihilo“.

6. Literatura

Každá učebnice speciální teorie relativity obsahuje diskusi setrvačné hmotnosti a její ekvivalence e energii. Jednoduchý, přitom fyzikálně velmi poučný výklad lze najít např. v knize Maxe Borna „Einstein's theory of relativity“, Dover publ., New York 1962 (ruský překlad Mir, Moskva 1964). Problémy energie a hybnosti v obecné relativitě jsou stále obsahem nejrůznějších přehledů a původních prací, nemá příliš smysl zde uvádět jen některou z citací. Historická („předeinsteinovská“) část našeho příspěvku je až na výjimky založena na knihách Maxe Jammera, Concepta of Mase, Harvard University Press 1961 (ruský překlad Progress, Moskva 1967), Philippa Franka, Philosophy of Scienca, Prentice-Hall 1962, a na článku Maxe von Laueho „Inertia and Energy“, otištěném ve sborníku Albert Einstein, Philosopher-Scientist, ed. P. A. Sehilpp, The Library of Living Philosophers 1949, paperbackové vydáni Cambridge University Press 1962.

O INTERAKCI A SÍLE

Bedřich Velický

Fyzikální ústav ČSAV

180 40 Praha 8, Na Slovance 2

1. Vzpomínka

Síla, fundamentální pojem Newtonova kosmu, je objekt záhadný a každý se s ní musí vyrovnat po svém. Mohlo se to stát i jindy, ale mne to potkalo ve III. semestru u elektrostatiky. Použil jsem svých prvých znalostí vektorové analýzy a zjistil, že popisy pomocí působení na dálku a za použití elektrostatického pole jsou rovnocenné, takže prokázat empiricky existenci (statického) pole je nemožné, třebaže tehdejší autority byly jiného názoru. Později jsem byl poučen, že takové diskuse mezi velikány skončily již v 19. století. Něco jiného byly elektrodynamické interakce. Ty jistě zprostředkovalo pole. Dokonce mohlo existovat samostatně, mít hmotnost... Interakce se materializovala, kvantovala na fotony, a to už byly jiné otázky. Ještě dvakrát mne Coulombův (či Newtonův) zákon r⁻² potkal: jenom ten dovoloval chápat náboj jako zdroj pole, jenom ten (a oscilátor) dával uzavřené orbity pro centrální problém. Usoudil jsem, že nejde jen o empirický poznatek, ale o nezbytnou součást harmonie světa.

2. Síly vnější a vzájemné

Druhý Newtonův zákon m a = F je tautologií, pokud nemáme nezávislý předpis pro sílu, danou buď z vnějšku, nebo jako resultantu vzájemného působení s jinými částicemi. První způsob nebezpečně navozuje představu síly jako příčiny pohybu. Protijed se často hledá právě ve vzájemných silových působeních. To však ne zcela stačí: pohyb celého systému je stále dán silami účinkujícími na částice, jenže ty jsou nyní určovány selfkonsistentním způsobem. Vnější síla na danou částici je jen speciálním případem; pochází od těch částí, na které částice nemá patrný účinek. Například Země a jablko se přitahují stejnou silou; jenže Země o to příliš nedbá.

Na správné místo staví sílu to, že ji nemůžeme měřit. Pozorovat lze pouze její dynamické účinky. Měřením pohybů lze zpětně, soudit na působící síly. To také přesně odpovídá srážkovým experimentům v atomové nebo jaderné fyzice: z asymptotických úseků rozptylových trajektorií se usuzuje na průběh srážkové interakce. Experimentální fyzika vůbec má ráz zobecnění inverzní rozptylové úlohy, zatímco teorie se pokouší o řešení úlohy přímé. Neshoda s experimentem často závisí hlavně na tom, že průběh sil nebyl empiricky dobře určen. Proto se teoretici stále raději obracejí k porovnání svých výsledků s počítačovými simulacemi, tedy s experimentálním studiem uměle vytvořeného kosmu, kde interakce jsou zvoleny člověkem-demiurgem a neshoda teorie s počítačovým experimentem odhaluje její nedostatečnost.

3. Psychologizující pohled na interakci

Pojmy síla a interakce jsou používány v řadě kontextů, dostatečně blízkých a zatížených subjektivními faktory, aby mohlo docházet k půvabným sémantickým konfúzím. Například duševní síla – telekineze. To zde pomíjím, jen mimochodem se zmiňuji o možném reciprokém jevu – ovlivnění psychiky manipulací s těžkými předměty.

Zabývejme se nyní pojmem interakce. Její projevy závisí na počtu zúčastněných částic a rozhodující předěly jsou N = 1, 2, 3, .... ∞ , alespoň pro interakce párové. To má těsnou analogii ve vztazích mezi (lidskými) subjekty, jak hned uvidíme na několika ukázkách.

N = 1 . Zdánlivě případ bez interakce, avšak pokud máme na mysli interakci prostřednictvím pole, potenciál k interakci tu je, dochází k polarizaci vakua a k renormalizaci vlastností částice („selfkonsistentní interakce“).

N = 2 . Ideální případ. Je-li přitahování silné, oba orbitují na uzavřené dráze. Jinak se trajektorie dočasně sblíží, pak zase oddělí.

N = 3 . V tomto případě se binární ovlivnění nemůže u žádné dvojice plně rozvinout vzhledem k rušení třetí částicí. Vzniká řada případů známých ze světové beletrie. Exaktní řešení možné jen v limitních případech. Tento počet tří částic již zahrnuje podstatné rysy všech malých systémů (N = 4, 5, ...).

N → ∞. U rozlehlých systémů se objevují nové kvalitativní rysy. Například saturovaná interakce: částice ovlivňují jen malé okolí, jejich vliv do dálky je stíněn. Párové působení je prostředím podstatně změněno, až v limitě může systém přejít v agregát nezávislých kvazičástic pohybujících se v efektivním středním poli ostatních. Tento ideální systém je ve skutečnosti pozměněn jednak korelačními opravami, jednak kolektivními ději. V soustavách mnoha částic je tedy původní (holá) interakce natolik zašifrována, že k odhalení její podstaty a jejího vlivu je zapotřebí nových prostředků. Ty byly dalekosáhle rozpracovány, avšak nepatří zatím k obecnému povědomí ani fyziků. To je jeden z významných problémů ve vytváření adekvátního obrazu světa.

4. Kvantová mechanika

Každý si jistě povšiml, že v kvantové teorii se síla objevuje zřídka. Je sice možné ji zavést a platí dokonce Ehrenfestova (kvantová Newtonova) rovnice

kde ‹...› označuje střední hodnoty operátorů. Bez znalosti vlnové funkce je však nelze stanovit, takže nevzniká uzavřená rovnice. Jsou ovšem zvláštní případy – volná částice, oscilátor, kvaziklasický pohyb. Celkově však využití pojmu síly není produktivní.

Interakce ovšem zůstává, ale k jejímu popisu nastupuje interakční energie jako člen hamiltoniánu v Schrödingerově rovnici. Tato možnost ovšem je v klasickém případě rovněž, avšak síla je tam názornější.

Účinky těchže interakcí v klasickém a kvantovém případě se velmi liší. Nenulová Planckova konstanta má za následek jednak kvantování energií, jednak nesilovou korelaci pohybu částic (Pauliho princip). Základní stav atomů i jejich agregátů se pak vyznačuje podstatně nenulovou kinetickou energií a konečnými atomovými rozměry. Systematické teoretické studium kondenzovaných soustav v posledních dekádách ukázalo jako svůj zásadní výsledek, že vlastnosti nejrůznějších látek, které byly původně fenomenologicky spojovány s různými typy sil: elektrostatických, van der Waalsových, kovalentních, výměnných atd., lze v podstatě redukovat na jedinou úlohu: popis soustavy elektronů a jader s coulombickou interakcí. Tato redukce připomíná poněkud překonání kinematické teorie pohybu nebeských těles (cykly a epicykly) Newtonovou mechanikou. V klasické elektronové teorii byla tato klasická teorie extrapolována z makroskopických do atomových rozměrů (blechy blech) za cenu zavádění stále nových fenomenologických konstant, vazeb a interakcí. Kvantová teorie jedinou změnou – správnou Planckovou konstantou – toto vše nahradila. Tento unifikační závěr je však dialekticky zastírán novým bestiariem kvazičástic a jejich interakcí. Tyto objekty nejsou zaváděny naplano – experimenty se slabě excitovanými látkami zpravidla vedou k údajům o kvazičásticích a jejich srážkách a přeměnách.

Na závěr Principií vytkl Newton pro budoucnost úkol vysvětlit kohezi a interakci v látkách, jakož i vliv vnějších agens. Je fascinující konstatovat, že k dosažení tohoto cíle bylo třeba právě tří století. Okruh těch, kteří si pravý dosah současných znalostí uvědomují, je omezený. Měli bychom usilovat o jeho rozrůstání.

Seminář
PEDAGOGICKO-FYZIKÁLNÍ DIALOGY
Skalský dvůr, 15.-18. 9. 1986

POCTA NEWTONOVI

Večer k 300. výročí
prvního vydání Newtonových Principií

Pondělí 15. září 1986, 19.30 hod.

Otevření výstavky newtonian

Zdeněk Horský

JANUSOVSKÁ TVÁŘ NEWTONOVSKÉ FYZIKY.

Přednáška ke stejnojmenému textu
uveřejněnému v seminárním tisku
„Pocta Newtonovi“

Newtonovské postludium

Chvilka hudby
proložené newtonovskými verši

Henry Purcell (1659 – 1695)
Sonáta pro trubku a smyčce
Pomposo – Adagio – Presto

POCTA NEWTONOVI

„Byl i sebeskvělejší vymoženosti budoucnost nám přinesla, sotva kdy bude překonáno dílo, které první nás poučilo o základním, veškerenstvo v souvislosti udržujícím zákonu světovém, sotva kdy budou překonána Newtonova Principia ! “

Augustin Seydler 1887 (1849 – 1891)

Večer „Pocta Newtonovi“ uvedl po vstupní hudbě Georga Friedricha Händela, doprovázející paralelní projekci newtonian a cambridgeských motivů, Jiří Langer:

Vážené kolegyně a kolegové,

dostalo se mi nezasloužené cti, že mám zahájit tento slavnostní večer. Naštěstí představovat oslavence je zbytečné a představovat řečníka je téměř zbytečné, protože asi všichni znáte doktora Horského z jeho brilantních přednášek o historii fyziky, jako autora krásné knížky o Keplerovi v Praze a jako spoluautora fyzikálního bestseleru Vesmír – takže prosím doktora Horského, aby se ujal slova.

JANUSOVSKÁ TVÁŘ NEWTONOVY FYZIKY

Zdeněk Horský

Astronomický ústav ČSAV 120 23 Praha 2, Budečská 6

Autorizovaný přepis magnetofonového záznamu přednášky (D1/96, D4/273) proslovené 15. září 1986.

Vážené shromáždění, vážení přátelé,

téměř se bojím začít, protože je ml naprosto zřejmé, že vůbec nejsem hoden té chvály, navíc nejsem fyzik a můj přínos je skutečně velice, velice malý. Má úloha je v podstatě předem známá – je dána titulem přednášky. To, co mohu a chci udělat, je především přehled těch nejširších historických souvislostí, které procházejí oním obrovským vývojovým uzlem, který Newtonovo dílo představuje. Záminka je celkem jasná. Letos je tomu tři sta let, co Newton podepsal – podle tehdejšího anglického kalendáře 8. května roku 1686 – předmluvu ke svému hlavnímu spisu Philosophiae naturalis principia mathematica. Myslím, že když už říkáme toto jedno datum – a historici si v datech libují – , rád bych uvedl, že je to téměř symbolické datum, protože Newtonův život je podle tohoto data bezmála symetrický. Newtonovi v tuto chvíli, ve chvíli podpisu předmluvy k Principiím, běžel čtyřicátý čtvrtý rok života a měl být živ ještě dalších jedenactyřicet let.

Když už jsem u těch dat, rád bych také uvedl, jaká jsou vlastně správná data Newtonova narození a úmrtí. Bude se asi o Newtonovi v souvislosti s Principii v tomto a příštím roce hodně mluvit a hodně psát a snad by bylo dobře, aby i v této věci byl pořádek a bylo jasno. Ta data se totiž uvádějí dvojím způsobem. To uvádění dvojím způsobem je správné – ale navíc se často uvádějí i data nesprávná, například v jediné české monografii o Newtonovi je zcela nesprávné datum úmrtí. Důvod k tomu, že data se uvádějí dvojím způsobem, je ten, že v Anglii tehdy nebyl přijat gregoriánský kalendář; byl přijat až v polovině osmnáctého století, a navíc nový rok počínal v Anglii 25. březnem. Newton, jak se někdy dočtete, se narodil prý na Štědrý den roku 1642, v témž roce, co umírá Galilei – jako by se tady předávala štafeta. Pokud jde o den Newtonova narození, nebylo to ovšem na Štědrý den, bylo to 25. prosince roku 1642 anglického počítání, což v našem přepočtu znamená 4. leden roku 1643; a datum jeho úmrtí je 20. března anglického počítání roku 1726, což je 31. březen našeho počítání roku 1727. Zemřel v Kensingtonu v Londýně jako význačný, všemi uctívaný muž, jako prezident Royal Society, když se byl narodil v malé vesničce ve Woolsthorpu jakožto pohrobek matce velice chudé, která od něj odešla, protože se brzy po jeho narození provdala jinam, a jeho výchovu převzala babička.

Snad jen několik málo údajů z jeho mládí: Jeho mládí bylo velice obyčejné, řekněme téměř nuzné. Vyznačoval se pouze tím, že měl zálibu v mechanických modelech a v mechanických hračkách. Fo běžném studiu se jako ne příliš nadaný nebo spíše ne příliš na sebe upozorňující dostal v roce 1661 na cambridgeskou univerzitu. Tam se teprve rozvinulo jeho nadání, takže o osm let později dostal už uvolněnou stolici matematiky.

V těchto osmi letech jsou dva zvláštní roky. Newtonovy životopisy jim říkají „morová léta“. Morová lata je takový jakoby hanlivý název, u Newtona to však byla nikoliv smrtící, ale naopak velice plodná léta, plodné období. Ten mor byl v Cambridgi a Newton jako spousta jiných kvůli nebezpečí Cambridge opustil, vrátil se do svého rodného Woolsthorpu, a tam v určité izolaci – někteří říkají „prý“, někteří říkají „skutečně“ – promýšlel základy toho, co jednou bude v životě dělat. Byla to zejména dvojí látka, a sice látka, která se týkala optiky, a látka, které se týkala dynamiky, nauky o pohybu těles, tedy toho, co jednou mělo vejít v Principia. Jak daleko je toto tvrzení pravdivé, je velice těžko, alespoň z našich pozic, dokládat. Názory jsou různé, nicméně jsou zachovány Newtonovy zápisky, v nichž jsou skutečně předjímány už takové formulace, jako slavné Leges motus, Zákony pohybu, a zdá se, že je i oprávněná domněnka, že mohou být skutečně vročeny do tohoto morového období, do těch let 1664 až 1666. Jistá věc je, že Newton krátce po návratu do Cambridge zkonstruoval v roce 1668 první model svého zrcadlového dalekohledu. O tři roky později ho dokázal zhotovit v takovém provedení, že byl schopen jej odeslat britské královské společnosti, což mu získalo značné renomé – 1671 byl zvolen členem Společnosti. To už byl tři roky profesorem v Cambridgi. Jeho další kariéra ho po dlouhodobém pobytu v Cambridgi přivedla do Londýna (1696), kde se pak stal vedoucím královské mincovny, a konečně od roku 1703 až do své smrti byl prezidentem Královské společnosti.

Na publikační půdu vstoupil Newton v roce 1671 krátkým pojednáním o optice. I to je taková dost význačná věc. Šlo skutečně o nikoliv knihu, ale v pravém slova smyslu vědecký článek. Co to je článek a jakou má roli, k tomu se ještě v naší přednášce vrátíme. Na počátku Newtona, abych to řekl tímto způsobem, byla tedy optika. Nicméně to, co činí Newtona Newtonem, není jeho dílo optické, ale jsou to rozhodně jeho Principia. Není to názor jenom Seydlerův, který jsme si mohli v úvodu dnešního večera z projekční stěny přečíst jako názor sto let starý, ale je to názor i dnes platný, a bude zřejmě s nejvyšší pravděpodobností platit stále. Proč? Skutečně pro nás Principia i dnes mají nesmírnou závažnost, protože v nich jsou zavedeny všechny ty základní pojmy, kolem nichž se ve fyzikálním dalším dění neustále točil život a které neustále přitahují naši pozornost. Snadno je zde kladeno rovnítko, přestože to rovnítko není zcela na místě, kterým to, co je obsahem Newtonových Principií, dostává označení Newtonova fyzika. To rovnítko není zcela na místě proto, že to není fyzika v plném rozsahu, a na druhá straně to taká není všechno, co Newton na fyzikální půdě vykonal. Právě v Principiích však jsou ty základní pojmy, které tolik znamenají, jako pojem čas, absolutní čas, prostor, absolutní prostor, pojem hmota – musíme mluvit tím historickým termínem – , je tu vymezeno, co to je těleso, je tu formulován gravitační zákon, je tu vymezeno, co se rozumí gravitačním působením.

Je skutečně otázkou, kdy Newton opravdu přišel na ty první myšlenky, které se týkají gravitační teorie. Všichni jistě znáte onu anekdotu nebo lépe řečeno soubor anekdot, které se toho týkají. Je to ona anekdota o jablku, a mělo se to stát v těch morových letech. Ať je tomu jakkoli, Newton se vrátil k táto problematice vlastně až koncem sedmdesátých let, snad pod vlivem dopisu, který dostal od svého přítele a současně hlavního rivala Roberta Hooka.

Mimochodem, Robert Hooke byl velice nablízku gravitačnímu zákonu, a nebyl to zdaleka jenom Hooke. (Já sám také jako mnoho jiných nejsem schopen rozhodnout, jestli mám označit Hooka jako Newtonova přítele nebo rivala nebo jako obojí. Kdo píše o Newtenovi, píše o Newtonovi jako o velké autoritě, o skvělém člověku, a o Hookovi přirozeně jako o jeho rivalovi, a zase naopak ten, kdo píSe o Hookovi, jednoduše zamění obě úlohy, jak už tomu bývá. AÍ je tomu jakkoli, rozhodně Hooke, který byl pracovníkem Royal Society, který tam začal jako zdatný experimentátor a za tu práci byl dokonce placen, byl zřejmě člověk, který v otázce pohybu došel velice daleko.) Dokázal Newtona, abyoh tak řekl, velice pobídnout, pokud šlo o práci o pohybu. Newton na problém sedl a v roce 1684 ohlásil na univerzitě přednášky, jejichž obsahem byla vlastně první kniha Frincipií, o rok později další kniha, a pak už nezbývalo nic než v tom našem jubilejním roce před třeni sty lety podepsat předmluvu k hotovému dílu.

O Newtonově díle, tedy především o Principiích, se mluví jako o obrovité syntéze. Základní prvky této syntézy jsou celkem jasná. Je to na jedná strana dílo Galilea Galileiho, který zvládl teorii pohybu těles při zemském povrchu, na druhá strana dílo Keplerovo, který zvládl kinematický popis pohybu planet v slunečním systému tak, že argumentu Sašu byl pak schopen přiřadit trojrozměrnou souřadnici planety. Tyto dvě hlavní složky se syntetizují v Newtonové díle, v Newtonových Principiích. Pohled o něco jemnější, který si dá za úkol zaznamenat všechno, co vešlo do té syntézy, musí však vzít v potaz podstatně víc. Především musí vzít v potaz to, co předcházelo tomuto stupni Kepler-Galilei. A toho je skutečně nesmírně mnoho. Pokud jde o výklad pohybu těles, ať už je to výklad řekněme pohybu těles při zemském povrchu nebo pohybu „vůbec“, je tu především rozsáhlé dílo nominalistů 14. století, Oresmovo, Buridanovo, anglická mertonské školy i tzv. „kalkulátorů“, které nikoli v hladině fyzikální reality, ale poněkud nesměleji v hladině teoretické „možnosti“ zkoumá různá vlastnosti pohybu, a to např. i pohybu rovnoměrně zrychleného. Jeden takový významný traktát, jehož autorem je Johannes de Hollandria, byl dokonce sepsán v 60. letech 14. století na pražské univerzitě. To je jedna taková větev, řekli bychom větev formálně matematická, která opravdu velice silně zapůsobila na mladého Galileiho, na to jeho pisanské, tedy to jeho první badatelské období, a skutečně vchází touto cestou do té naší budoucí syntézy.

Je tu ovšem i větev jiná. To je taková, která uvažuje o gravitaci jako přitahování, jako přitahování čeho čím, kdy vůbec poprvé se nám objeví přitažlivost. Přitažlivost je přirozeně dávno známá a je vědecky zvládnuta. Rád bych podtrhl to vědecky, protože ta teorie, která to popisuje, přestože bývá dnes citována s pejorativním přízvukem, teorie Aristotelova, skutečně je ve své propracovanosti a důslednosti vědecká.

V Aristotelově systému skutečně působí attractio, přitažlivost. Ale jak funguje? Co přitahuje? Ta přitažlivost není žádným způsobem spojena s materií, s hmotou, rozumí se s hmotou v tehdejším smyslu. Přitažlivost je předem vložena do celkového schématu kosmu: To, co přitahuje, je prázdný bod, je to střed vesmíru.

Udělejme si na chvíli takový myšlenkový pokus, který nám okamžitě rozliší mezi tím, od čeho vlastně vycházíme, pokud jde o přitažlivost, což je ona původní koncepce Aristotelova, a tím, kde budeme dnes končit, oož je Newton. Mějme Zemi,, a vyzvedněme ji na chvíli z jejího místa. V tom aristotelském systému je to ze středu kosmu. A mějme někde na jiném místě kámen a volně ho pustíme. V tom aristotelském výkladu to bylo tak, že pokud Země byla na svém místě, ten kámen padal po svislici k Zemi. V našem newtonovském popisu je to přirozeně naprosto stejné. Jestliže ale teď tu Zemi vyzvedneme, a necháme ji v jiném bodě setrvávat, potom v tom aristotelském systému ten kámen bude zase padat tam, co byla před svým vyzvednutím Země, protože tam je střed kosmu. Ten střed tíže jsme nemohli přestěhovat tím, že jsme stěhovali Zemi, ten tam je zakódován jednou pro vždycky v tom místě, kde je střed kosmu. A jak to dopadne? Nu – dopadne to stejně jako předtím. Země, kterou jsme vynesli, musí pospíchat k tomu středu tíže, tam je její přirozené místo. A protože je mnohem těžší než ten kámen, bude tam podle pravidla, že tělesa těžká padají rychleji než tělesa lehká, dříve než ten kámen. A ten kámen dopadne na totéž místo Země jako v tom předchozím případě. To je počátek úvah o attractio, o přitažlivosti. Jak to dopadne v tom newtonovském případě, snad nemusím říkat, to je zbytečné. Tento myšlenkový pokus není snad nějaký dodatečný výmysl. Rád bych upozornil, že jeho první polovina, nenewtonovaká, je obsažena už v Ptolemaiově Almagestu.

Tak to tedy vypadá poprvé, kdy se setkáváme s gravitací. Přitažlivost se nám objeví ve zřetelně jiném pojetí, poprvé jakžtakž spojena s materií, až u renesančních platoniku v patnáctém století, kdy Marsiglio Ficino zakládá svou nauku o přitažlivosti na pojmu cognatio, na pojmu příbuznost. Příbuzná látka přitahuje své součásti. Ficinův vesmír je stále ještě plný těch starých elementů, živlů, jako země, voda, vzduch, oheň, a funguje to tak, že voda přitahuje částečky vody, země částečky země a tak dál. A kupodivu, přirozeně stále ještě v tom ficinovském kosmu, pořád ten střed Země je ten jediný bod, kam směřuje to vůbec nejtěžší. Ha rozdíl od toho Koperník – a Newton přirozeně nestaví na ničem jiném než na koperníkovském heliocentrickém systému – Koperník poprvé stanoví víc center tíže, která jsou spojena s určitou hmotou. Zachovává se přitom stále to cognatio, ta příbuznost. Tedy nejen Země, ale i planety budou přitahovat – ale co? Pouze své součásti. To, co bude utrženo například z Venuše, se bude vracet na Venuši. To, co bude utrženo z Jupitera, se bude vracet na Jupiter. A pokud aspoň na některá planety vidíme, přesvědčujeme se o jejich kulové formě. Koperník vidí pouhýma očima bezpečně na dvě tělesa, Slunce a Měsíc, která mají kulovou formu – nejsou to planety než jen v tom starém tradičním smyslu; o skutečných planetách si Koperník jen myslí, že mají kulovou formu. Ta kulová forma, kterou zachovávají, má být způsobena právě tou gravitací, gravitatio, tento pojem je tam skutečně užit.

Jak je tomu dál? Velice pregnantně je pojem přitažlivosti formulován v roce 1609 nebo spíš už 1608 v Praze Keplerem. Kepler dopsal Novou astronomii 1605, vyšla až 1609, především proto, že nebyly penise, .za které by bylo možno knihu vydat. Mezitím vytvářel nejrůznější teorie o tom, jak se pohybují planety. Teorie, která zde byla dnes už jednou citována doktorem Loosem, tvrdí, že je to Slunce, které uvádí planety do oběžného pohybu. Kepler předpokládá, že ta síla, která pohybuje planetami, má sídlo ve Slunci, předpokládá, že Slunce rotuje, že rotuje ve stejném smyslu, jako obíhají planety kolem Slunce, a tedy předpokládá, že Slunce nějak planety pohání, že je nějak po těch jejich drahách „smetᓹ. Předpokládá, že jde o jakési magnetické působení. Ten magnetismus tady má pořád svou významnou úlohu, přestože vlastně vstupuje do fyzikálních úvah s oblasti tak zvané magie. Je to magia naturalis, přírodní magie, kterou dělá zejména Giambattista Porta a na niž navazuje William Gilbert. Odtud je vlastně poprvé vzato ono actio in distans, působení na dálku, bez kterého by Newton těžko mohl pracovat. To je to, co Kepler předpokládá. Slunce rotuje – on to zatím ještě neví, on to musí předpokládat – , a tedy pohání planety. Naštěstí se mu připlete do cesty v Praze Jan Matouš Waoker z Waokenfelstu, Brunův stoupenec, a ten Keplera uvede na myšlenku, jak by to asi vlastně vypadalo, kdybychom se mohli podívat na vesmír, hlavně na Zemi, z Měsíce. Viděli bychom, že Země rotuje, ale co bychom viděli všechno ostatního? Kepler rozvíjí tu myšlenku dál – jak bychom se na ten Měsíc dostali – , a tady poprvé začne sám Kepler uvažovat o vztahu Měsíc-Země. A zatímco předtím uvažoval o vztazích planet a Slunce, a to Slunce kladl vždycky do jiné, hierarchicky vyšší kategorie,než jsou planety, tak najednou Měsíc a Země v tehdejších představách a v Keplerových rovněž jsou tělesa v podstatě stejnorodá. Tak co z toho bude?

Kepler začne přemýšlet, a říká: Kdyby hustota obou těles byla stejná, tak jejich masy by byly v tom a v tom poměru, a ony by na sebe navzájem působily, přitahovaly by jedna druhou. Říká dokonce i toto: „Jestliže by byly umístěny někde ve světě v některém místě dva kameny blízko sobě, mimo dosah působení třetího příbuzného tělesa (to ficinovské „cognatio“ je tu pořád ještě ve hře), tyto dva kameny by se podobně jako dvě magnetická tělesa sešly na prostředním místě, a přitom by každý z nich přistoupil k tomu druhému o takový úsek, jaký odpovídá hmotnosti (smíme-li takto přeložit) toho druhého vůči prvnímu.“ Co chcete v podstatě víc? To je anticipace Newtonova zákona. Je velice, velice pregnantní. Stačí jenom pokračovat. A tady se ukazuje, „jak mnoho experimentální fyzika působí ku pokroku vědy a jak podporuje rozvoj teorií“. Hned o dva roky později obrátil Galilei dalekohled na Slunce, našel skvrny, viděl, jak Slunce rotuje, viděl, že rotuje ve stejném smyslu, jak obíhají planety kolem Slunce. Čili Kepler už nemusel mít domněnku, nýbrž – měl jistotu. Proto se vrátil ke svému starému „magnetickému“ výkladu pohybu planet a myšlenku gravitačního působení již nikdy dál nesledoval. Tedy nejen Kepler nedovedl ten svůj gravitační zákon k cíli, své myšlenky nedovedl k cíli zřejmě ani Robert Hooke. Zřejmě kromě Newtonova génia nikdo nevložil myšlenky Keplera, Hooka a možná i jiných o gravitaci, ani oni sami, do tak promyšleného a skloubeného díla, jako jsou Newtonova Frincipia. Dá se dokonce říci, že tady v Newtonových Principiích je konečně zlikvidován onen starý přežívající protiklad té syntézy Galilei-Kepler, to znamená pozemské pohyby a proti nim nebeské pohyby, tedy ten starý aristotelský protiklad sublunárního a supralunárního. Ale přece ještě není. Ještě tak doslova není, on stále ještě – ale již naprosto zdůvodněně a oprávněně – přežívá v tom, že Newton je nucen zvlášť pojednávat o pohybu těles, jimž je kladen odpor, tedy o pohybu těles v pozemském prostředí, a pohybu těles, jimž odpor kladen není, což jsou planety. A to, aby mohl takto postupovat, si také vyžádalo dlouhý vývoj. Koperníkova představa v polovině 16. století byla ještě taková, že počítal, vědomě počítal s tím, že je možno celý systém materializovat v tom smyslu, že je proveden v tuhé hmotě; že planety nebudou obíhat, ale že budou skutečně neseny tuhými sférami, v nichž jsou zasazeny tak „jako suk v prkně“. Stojí to hodně času a musí pomoci náhoda, aby se v důsledku Tychonových observací velké komety v roce 1577 tomuto astronomovi podařilo prokázat, že tato kometa by musela při svém pohybu tuhými sférami procházet, že by je musela rozbíjet, že tedy jako tuhé nemohou existovat. A tak se ty sféry rozplynuly v jakési plynulé médium, kde se planety pohybují „jako ryba ve vodě“. A teprve hodně dál musí toto prostředí řidnout, aby u Keplera bylo něco jako aura coelestis, či aura aetherea, nějaká taková neurčitá prostředí. A musí přijít takoví lidé jako Torricelli, Pascal, a i Guericke s magdeburskými polokoulemi, aby byla prokázána možnost existence vakua. A teprve ve vakuu se planety mohou pohybovat ve shodě s těmi Newtonovými představami jako tělesa,„quibus non resistitur“, jimž není kladen odpor. Bez prokázání existence vakua by Newtonova syntéza rovněž nebyla možná.

To ovšem taká ještě není celá ta newtonovská syntéza. Ta newtonovská syntéza nám klade otázku, do jakého prostoru vložil Newton ten svůj svět. A on ho vkládá do eukleidovského prostoru. Poprvé. Poprvé vůbec, ještě ani ten koperníkovský ani keplerovský prostor není eukleidovský prostor. Eukleidovský prostor nebyl fyzikálním reálným prostorem až po Newtona. U Aristotela přirozeně nebyla homogennost, nebyla izotropnost, byly preferovány směry od středu ke středu, byl preferován střed jakožto jeden singulární bod. Totéž vlastně zůstává u Koperníka, protože je tu omezení, pevná sféra stálic, a je tu střed, obsazený Sluncem. A u té výjimečnosti Slunce i Kepler stále ještě zůstává. Tady je potřeba vzít v úvahu to, co s úvahami o prostoru provedl Giordano Bruno, který vlastně je tou osobností, která pro zažitost těch základních myšlenek kopernikanismu udělala velice mnoho. A to přesto, že by se dalo říci – nejen dalo říci, oni to jeho současníci říkali velice tvrdě – , že není žádný vědec. Ale ta realizace, fyzikální realizace eukleidovského prostoru, to je skutečně dílo Brunovo.

Tedy z tohoto hlediska přijímá newtonovská syntéza všechno to bohatství, co jsme uvedli. To všechno vchází z jedné strany do té janusovské brány, to obrovské množství toho, co se vyvíjí v předchozí přírodovědě, v předchozí fyzice. Co vychází na druhé straně? Na druhé straně toho vychází velice málo. Sice Principia jsou nesmírně podstatná, jak jsme si tu řekli. Ale je to fyzika? Především: je to celá fyzika? To přece zdaleka není celá fyzika. Všichni mi namítnete, že v názvu Principií je philosophia naturalis, přírodní filozofie, ale philosophia naturalis, natural philosophy znamená v angličtině víceméně stále ještě fyziku. Znamená – neznamená – Principia nejsou celá fyzika. Je tu přece zvlášť, mimo Principia, Newtonova Optika, a ani Newton nezná vazby mezi svou dynamikou a svou optikou. Kde je termika? Kde je nauka o elektřině, kde je nauka o magnetismu, kde je akustika? To jsou tehdejší reálné, nebo aspoň v tom pojetí, jak lze fyziku počítat řekněme v osmnáctém století, to jsou reálné fyzikální discipliny. Ty tady zatím nejsou, neprošly s sebou tou janusovskou branou.

Fyzika v pojetí sedmnáctého století je rovněž něco jiného, mnohem komplexnějšího. Vezměme si příklad fyziky přímo nazvané Fyzika. Physica ad lumen divinum reformata, Physicae synopsis ad lumen divinum reformatae od Jana Amose Komenského: první vydání 1633, a pak řada vydání až do Komenského smrti, a dokonce ještě dál. Tato fyzika obsahuje mnohem víc, zahrnuje i živou přírodu, ba i psychologii. Poněvadž celá příroda je fysis, a všechno, co se zabývá fysis, je fyzika.

Kdežto Newtonovou janusovskou branou prochází něco, co se dostalo – obsahově i metodicky – do obrovského předstihu. Je to jen část fyziky, zato v této chvíli část nejpodstatnější – mechanika. To, co jsme tu dnes slyšeli od Br. Pekárka, že už vzniká obsahově plná syntéza na poli fyziky, to je vlastně teprv jakoby splácení dluhu oborům, které tehdy neprošly janusovskou branou spolu s Newtonovými Principii. Protože ten přístup k fyzikální problematice, který Newton zavádí, to je vlastně něco podobného jako to, co se v astronomii jednu dobu jmenovali; metoda vybraných polí. Soustředíme se jen na určité problémy, v nichž je možno právě teS jít kupředu, a jimi se budeme především sabývat.

I problémy je možno dělit. Jeden problém – jeden článek. Probádané malé úkoly se teď nově budou publikovat jako články. A tak Newton jako jeden z prvních vystupuje navenek, vůči vědecké veřejnosti. Všimněme si i etymologie toho slova článek, Artikel. Vyjadřuje, že i poznání je najednou rozděleno, artikulováno.

Ale týž Newton sám napsal spoustu svých osobních poznámek, které teprve v posledních letech, v posledních desetiletích jsou systematicky zkoumány (určitou dobu nebyly systematicky zkoumány a výsledky zveřejňovány snad také proto, jak se mezi historiky šuškalo, že britská královská společnost si nepřeje a klade překážky, aby vedle toho dokonalého a jasného Newtona někdo zahlédl toho Newtona temného – na stránkách, kde jsou úvahy teologické, alchymické, astrologické, a všechno možné). V těchto osobních poznámkách je také jeden výrok, který bohužel není datován, alespoň mně se nepodařilo sehnat přesnou dataci, ale myslím, že stojí za to, abych ho ocitoval. Je to upřímný výrok Newtonův o vědě i o sobě samém, a říkáš „Objasnit celou přírodu je příliš obtížným úkolem pro jediného člověka i pro jediné období. Je lépe dokázat sice málo, ale s jistotou, a ostatní přenechat těm, kdo přijdou v budoucnosti, než objasňovat všechno.“ To je tedy přímo heslo, které zřejmě věda rovněž přijala současně s tím newtonským dědictvím. Je zde upřímně a jasně konstatováno, že přírodu poznáváme po částech, či ie s přírody poznáváme jen části. Ale jasně cítíme, že toto heslo potřebuje nějakou protiváhu.

Podívejme se rovněž na to, jak procházejí tou janusovskou branou některá taková základní pojmy anebo přímo některá základní koncepce. Na obou stranách té janusovské brány se mluví o jednotě mikrokosrnu a makrokosmu. Před Newtonem to ovšem znamená něco úplně jiného než po něm. Před Newtonem je to představa především paracelsovská, kde ten makrokosmos je celý vesmír, ovšem celý vesmír v tom starém středověkém, geocentrickém pojetí, a ten mikrokosmos je člověk s jeho vztahy mezi vesmírem a člověkem, vztahy, které mohou být nejrůznější. Je možné studovat je vědecký, ale patří sem například v tehdejším pojetí i celá astrologie. Po tom průchodu tou janusovskou branou je tu jednota mikrokosmu a makrokosmu také jako určitý slogan, jako nálepka nad něčím, ale znamená už něco docela jiného. Znamená jednotu velkého i malého, a v obém – jako příklad vezměme pád těchto hodinek na stůl a vztah Země-Měsíc nebo Země-Slunce – je to řízeno stejným způsobem. Platí stejné zákony pohybu. Není už zásadního rozdílu mezi tím ve velkém a mezi tím v malém, tady je prostě nade vším nadvláda mechanického pohybu. Taková nadvláda, že jsme jí byli do té míry zmateni, že jsme považovali mechanický pohyb, jak jsme se to naučili v minulém století, v klasifikaci pohybů za ten nejjednodušší pohyb vůbec. Úplně jsme přehlédli, že se nám jeví nejjednodušším proto, protože jsme ho historicky nejdříve uchopili, zatímco v té objektivní klasifikaci jemu jakožto pohybu shluků molekul přísluší nějaké střední místo mezi těmi mega- a mezi těmi mikropohyby v tom našem pojetí.

Na jedné i na druhé straně té janusovské brány se mluví o jednotě mikrokosmu a makrokosmu. Ale ten mikrokosmos před janusovskou branou je mikrokosmos živý, je to především člověk, který má vůli, který koná, který je činitel, je to homo faber, činící, tvořící člověk. Zatímco ten mikrokosmos, který prošel tou janusovskou branou, je umrtven, je mrtev. Tady se uplatňuje velice řekl bych to tvrdé zasažení do základní koncepce přírodovědy. Proces mechanizace a proces matematizace přírody, jehož hlavním protagonistou je skutečně Newton, vyžaduje, aby byla, abych tak řekl, vytvořena ontologická záruka, že ty přírodní děje budou probíhat skutečně vždy pouze jednoznačně. To znamená: Podařilo-li se třeba Newtonovi sjednotit zákony, podle nichž se pohybují pozemská tělesa i celá planetární soustava, je třeba sjednotit nejen formulaci těchto zákonů, ale je potřeba sjednotit i ten substrát, který tomu sjednocujícímu zákonu má podléhat. Je potřeba, aby ten substrát ze sebe sama nikdy nevnesl nic do toho přírodního děje. On mu musí podléhat naprosto mrtvě, naprosto slepě, tedy sám musí být mrtvý. Na to narážíme vlastně už tehdy, když Galilei začíná uvažovat o inercii. Jeho inercie nesměřuje jen k principu setrvačnosti v tom našem smyslu. Co to je inertus? To naše slovo, české slovo setrvačnost je pro nás spojeno spíš, ale ne právem, s představou pohybu. Co je to setrvačník? Setrvačník je spjatý s představou pohybu. Nebo se řekne: setrvačností vyletěl z havarovaného auta, čili zase pohyb. Ne! Inertus je líný. Lenost, nečinnost, neschopnost činnosti, to je ten pravý sémantický smysl té inercie. A tedy ta příroda bude mrtvá a bude zkoumána jako mrtvá. Jako mechanicky pracující stroj. Dokonce už před Newtonem, 1628 píše William Harwey o té jedné velké pumpě. Srdce je pumpa. Galilei píše o tom, jaký průřez musejí mít kosti, aby unesly tělo, – je to architektura, jsou to páky, je to v podstatě neživá fyzika, aplikovaná na živé tělo. A přirozeně v důsledku toho může vzniknout i ten La Mettrieův 1'homme machine. To je rozklad koncepce živé přírody, to je počátek mechanického materialismu.

Na jedné straně je tedy velice významná syntéza, ta syntéza, kterou například Max von Laue hodnotí přímo jako kritérium pravdivosti fyzikálního poznání světa, syntéza, která se stává vzorovou, která se poprvé uplatňuje jako velmi účinný prostředek, když syntetizuje dynamiku Galileiho s keplerovskou kinematikou, podruhé se stává v třicátých letech minulého století podobným nástrojem, když nauka o magnetismu a nauka o elektřině se spojí, a začlení se pak i optika, a tak to běží dál. Je to vlastně jeden ze základních obratů – prosím vás promiňte, tady mluví historik do fyziky, kaji se za to – jeden ze základních obratů fyzikálního poznání. Ale – na jedné misce vah je ta trvalá hodnota této syntézy, na té druhé je ta dezintegrace. Dezintegrace fyzikálního obrazu světa na jednotlivé fyzikální discipliny, mezi kterými po celé osmnácté století nebylo žádné vazby. Ani Newton se nevzrušuje tím, jaké vlastně jsou vazby mezi jeho dynamikou a mezi jeho optikou. Ani ho netrápí otázka, jak se mu to vlastně obojí do jednoho a téhož vesmíru vejde, a proč si to nepřekáží. Možná tu otázku kladu hloupě, ale my jsme už takoví, že nás by podobná otázka spíš napadla. Tedy to jsou ty daně, které se tu platí za takovouto syntézu.

Nicméně mechanika se vůči ostatním fyzikálním disciplinám nechová macešsky. Je pro ně vzorem a oporou. Stačí jen vzpomenout na tvar Coulombova zákona v elektrostatice a v nauce o magnetismu, abychom věděli, oč tu jde.

Navíc, vzpomeňme ještě na tu určitou dobu, kdy se to všechno děje. Děje se to v situaci, kdy Newton je vlastně už vědecký pracovník nového typu. Je to člověk, který do své obživy zapojuje, abych tak řekl, svůj mozek. Je jakožto vědecký pracovník zaměstnáván, společností registrován. Věda je institucionalizována. Existuje státní akademie, on je do ní zapojen, pracuje v ní, má své spolupracovníky, má své rivaly. Hodnotí se priorita. Hodnotí se formulace. Jeho formulace jsou, a to je známé, velice opatrnické. Spousta otázek není dořešena. A kdybychom Newtonovi nebo Newtonovu dílu položili otázku, zda je to taková opatrnická, do jisté míry sektářsky držená věda, možná, že sám by to přiznal. Je k tomu tlačen určitou situací. Co za Newtona samotného nejlépe mluví, je fakt toho temného, nepublikovaného, teprve nyní po kusech zveřejňovaného neznámého Newtona, kde on sám si tuto situaci uvědomuje, kde se jí znepokojuje, kde se za ni omlouvá, kde sám, řekněme, bádá o věcech, které ho zajímají, které překračují to omezení těch vybraných polí, která vlastně on sám především stanovil a v nichž vývoj jde prudce kupředu. Myslím, že není hezké, jestliže nakonec uvádím právě takovéto hodnocení, které není zrovna nějaké líbivé. Není líbivé, i když pro Newtona je metodicky a morálně vnitřně zcela zdůvodněno a vysvětleno, když Newton aspoň sám sobě řekne, aby se ospravedlnil sám před sebou, že objasnit celou přírodu je příliš obtížným úkolem pro jediného člověka. Je lépe vykládat sice málo, ale s jistotou, a ostatní přenechat těm, kdo přijdou v budoucnosti, než objasňovat všechno. Možná, že tady je úloha, kterou nám Newton předal. Ten citát má zřetelně dva póly. Je tu stanoveno, jak máme postupovat, je tu však také naznačeno, čeho se máme obávat. Trhá se jednota poznání, trhá se úplnost poznání. A Newton sám, který navenek vystoupil brilantními, ale dílčími Principii, se o tuto jednotu a úplnost sám v sobě obával. Zdá se, že Newton i tady cítil, že se něco trhá, že se trhá jakýsi dialog. Dialog jednoho oboru s ostatními obory, že se nějak trhá dialog přírodovědy řekněme s tou širší veřejností, že se zanedbává požadavek, aby výsledky přírodovědy nebyly jen odbornicky vyjádřeny, ale aby veřejnost věděla, jak se to dělá a k čemu to je.

Dovolte mi již jen závěrečnou osobní poznámku: Mni osobně se velice líbí a velice si vážím toho, že na těchto Dialozích je tolik místa, myslím po právu tolik místa věnováno relaci mezi fyzikou a kulturou. Myslím, že jedním takovým úkolem je zachovat ten dialog mezi fyzikou a kulturou a že snad není nemístné, jestliže na to vzpomeneme i v přednášce k výročí Principií.

Děkuji Vám za pozornost.

J. Langer: Děkuji doktoru Horskému za velice krásnou přednášku. – Teď jsme slyšeli mnohokrát jméno Newtonovo v řeči prozaické, nyní uslyšíme třikrát Newtonovo jméno v řeči vázané, a sice postupně ve verších Alexandra Popea, Williama Blakea a Vítězslava Nezvala.

Příroda se svým řádem spaly v tmě;
Bůh „Budiž Newton“ řek' a světlo je.

I. Pomposo

Tak strašlivé pokolení Losa a Enitharmony dalo
zákony a náboženství synům Karovým, víc a víc je
poutalo k zemi, zavíralo a omezovalo,
až filosofie pěti smyslů byla hotova.
Urizen zaplakal a svěřil ji do rukou Newtonovi a Lockovi.

(Ze sbírky „Afrika“ Williama Blakea; překlad Z. Hron, četl J. Hollan.)

II. Adagio

Tisíc jablek spadlo na nos zeměkoule
a jen Newton doved těžit ze své boule
tisíc lidí mělo epilepsii
a jen svatý Pavel uzřel hostii
tisíc hluchýoh lidí bloudí beze jména
a jen v jednom z nich jsme našli Beethovena
tisíc šílenců již táhlo zámořím
a jen Nero doved zapáliti Řím
tisíc vynálezů jde k nám za sezónu
jenom jeden z nich však byl ten Edisonův
Tisíc jablek spadlo na nos zeměkoule a jen Newton doved těžit ze své boule

(Z Nezvalova „Edisona“; četla M. Fojtíková.)

III. Presto

Isaac Newton:

„Nevím, jakým se budu zdáti světu,
sobě však připadají jako chlapec,
jenž si pohrával na břehu mořském
a jenž se bavil tím, nalezl-li
občas hladší oblázek neb
pěknější lasturu než obyčejně,
kdežto veliký oceán pravdy
ležel neodkrytý u mých nohou.“

FYZIKA JAKO SOUČÁST KULTURY

Jiří Langer

Katedra matematické fyziky MFF UK 180 00 Praha 8, V Holešovičkách 2

Vnutí-li se člověk, který toho ví o umění ještě méně než o fyzice, s přednáškou podobného názvu, cítí potřebu se omlouvat. Tedy, jak jsem se k tématu dostal.

Zhruba před sedmi lety uspořádala redakce Kosmických rozhledů diskusi o vztahu astronomie a umění mezi vědeckými pracovníky a různými představiteli kulturního života /1/, o tři roky později se podobné setkání opakovalo /2/. Na obou setkáních jsem byl požádán o úvodní slovo k jednomu z témat a věnoval jsem proto přípravě určité studium a přemýšlení. Duch obou setkání mne přesvědčil, že mezi fyziky, tvůrčími umělci i humanitními vědci je řada otázek společného zájmu, a proto doufám, že má přednáška na tomto fóru může přinejmenším poskytnout zajímavou látku k přemýšlení.

Ve svém slovníkovém významu slovo „kultura“ znamená „souhrn všech materiálních a duchovních hodnot lidstvem vytvořených“. V tomto smyslu není samozřejmě pochyb, že fyzika ke kultuře patří, právě tak jako výroba piva, oběžníky ministerstva školství aj. V běžném užívání má ovšem slovo „kultura“ podstatně užší význam, obvykle se pod ní představuje umění a některé humanitní discipliny. Vezměme např. spojení „kulturní pracovník“; nevím, zda umístění Planetária v Parku kultury a oddechu souvisí s prohlášením astronomie za kulturní, nebo oddechovou disciplinu.

Mohlo by se zdát zbytečné vést diskusi o tom, zda fyzika ke kultuře patří či nepatří. Jenže slovo kultura má v běžném užívání poněkud tendenční nádech, odpovídající jeho původu z latinského „zušlechťování“; jistě nás trochu mrzí, že obecný soud asi fyziku za příliš zušlechťující disciplinu nepokládá. Vezměme např. spojení „kulturní člověk“ a snažme se odhadnout výsledek ankety s dostatečně širokým okruhem respondentů, jaké atributy má kulturní člověk mít. Pravděpodobně by od něj byly požadovány určité znalosti a zájmy z oblasti umění a některých humanitních disciplin, dále to, že při jídle neolizuje nůž a chodí řádně upraven. Asi by panovala shoda i v tom, že má věřit, že Země je kulatá a točí se kolem Slunce. Má ale znát druhou větu termodynamickou? Poslední otázka by jistě vyvolávala úsměv.

Příklad druhé věty jsem nezvolil náhodně. Ve studii „Dvě kultury“ /3/ líčí C. P. Snow, úspěšný fyzik, který se stal úspěšným spisovatelem, jak s výše zmíněným výsledkem zjišťoval znalost druhé věty u svých intelektuálních přátel. Spolu se zanedbatelnými fyzikálními vědomostmi u „literárních intelektuálů“ shledal Snow i malé znalosti umění – s výjimkou hudby – u svých přátel fyziků, jeho hodnocení však vyznívá v důležitém aspektu v jejich prospěch. Zatímco vědci přiznávají malou sečtělost s určitými rozpaky, jejich intelektuální protějšky se dívají na znalost fyziky jako na něco zbytečného a neuvědomují si, že neznalost druhé věty termodynamické je – stále Snowovými slovy – neznalostí stejného druhu, jako když někdo neví, co napsal Shakespeare. Jejich postoj v řadě případů je navíc nejen ne-vědecký, ale i protivědecký. Slovo „intelektuální“ zde užíváme ve shodě se Snowem ve smyslu ironické poznámky známého matematika G. H. Hardyho: „Všiml jste si, v jakém smyslu se dnes užívá slova ,intelektuální‘ ? Zdá se, že existuje nová definice, která jistě nezahrnuje Rutherforda, Eddingtona, Diraca nebo mne.“

Snow hovoří o existenci dvou kultur, „intelektuální“ a „vědecké“, jejichž představitelé si navzájem nerozumějí. Konstatuje tuto situaci jako fakt, ale jako fakt škodlivý a nepříjemný a rozebírá jeho příčiny. Vidí je v tom, že umělci obecně nepochopili význam „I. a II. industriální revoluce“ a v tradici anglického systému vzdělávání. Já se nebudu snažit o hlubší rozbor příčin rozkolu, i když v první části budu stručně sledovat jeho vývoj, převážně na poli literárním. Spíše bych chtěl ukázat, že mezi duchem umění & fyziky není zdaleka tak propastný rozdíl, jak se někdy soudívá, že si mají rozhodně co říci a že tento dialog může být užitečný pro obě strany, že řada zdánlivých antagonismů je založena na neporozumění. Nebo ještě spíše, pokusím se dát podněty k zamyšlení po této linii.

I. Vznik a vývoj trhliny

Nature and Nature's laws lay hid in night.
God said, “Let Newton be” and all was light.

Příroda se svým řádem spaly v tmě.
Bůh „Budiž Newton“ řek' a světlo je.

Dvouverším Alexandra Pope (1688 – 1744) v překladu Z. Hrona jsme vstoupili rovnou do newtonovské doby, kdy fyzika již byla svébytnou disciplinou. Verše dokumentují nadšení, které newtonovská fyzika budila v intelektuálním světě století rozumu. A jistě právem. Dnešní student většinou není příliš fascinován, když se musí učit Newtonovy pohybové zákony. Možná ale, že by spíše dokázal toto nadšení sdílet, kdyby si uvědomil pronikavou změnu obrazu světa, která se utvářela přes Descartese, Keplera, Galileiho á vyvrcholila v Newtonově díle. Sudice spřádající nit osudu byly odedávna inspirací umělců i předmětem kontraverzí filosofů. Newtonovská fyzika najednou předložila obraz světa předpověditelného, obraz krásně shrnutý ve známém výroku P. S. Laplace, že intelekt, který by byl dostatečně obsáhlý, aby uměl podrobit data analýze, by měl před sebou budoucnost celého vesmíru právě tak jako jeho minulost.

Rozsáhlejší rozbor dopadu newtonovské teorie na filozofii i umění věku rozumu najdeme např. v /4/. Když jen náhodně listujeme anglickou poezií 18. století, překvapí nás, jak často se setkáme se slovem „science“. Jeden z vůdčích literátů newtonovské doby John Diyden napsal:

„Člověk musí být vzdělán v několika vědách a musí mít rozumovou, filozofickou a do jisté míry i matematickou hlavu, aby byl dokonalým básníkem.“

Citát je pro fyziku – která tehdy reprezentovala nejdůležitější „science“ – jistě velmi lichotivý. Odpůrce by mohl namítnout, že zmíněný vliv byl záporný, protože Dryden zaujímá sice v anglické literatuře důležité místo díky svému vlivu, ale jeho poezie není dnes příliš čtena. Nejsem kvalifikován pro to, abych se pokoušel o hodnocení Drydena a jeho školy, něco k němu řekne citát L. I. Bredvolda, který uvádím v další části přednášky. Je však myslím nesporné, že např. faustovská filozofie činu je pozdním dítkem klimatu, které se vytvořilo ve „věku rozumu“ díky vědě a fyzice především.

V českém překladu Popeova dvouverší vypadlo důležité slůvko „all“. Slůvko vypadlo z metrických důvodů, ale rozdíl mezi překladem a originálem vlastně dobře vystihuje rozdíl mezi dnešním hodnocením fyziky, a to nejen newtonovské, a nadšením věku rozumu, který nadhodnocoval univerzálnost klíčů, jež má věda v rukou k racionálnímu výkladu světa. To bylo jedním z důvodů (samozřejmě zplošíuji a pomíjím řadu důležitých historických souvislostí), jež vedly k romantické reakci. Ta šla se svou kritikou nedostatečnosti mechanistického výkladu světa až k odmítání racionálního výkladu světa vůbec:

Tak strašlivé pokolení Losa a Enitharmony dalo
zákony a náboženství synům Harovým, víc a víc je poutalo
k zemi, zavíralo a omezovalo,
až filosofie pěti smyslů byla hotova.
Urizen zaplakal a svěřil ji do rukou Newtonovi a Lockovi.
(William Blake (1757 – 1827), „Afrika“, přel. Z. Hron)

Urizen (= your reason) představuje v Blakeově symbolice rozum, umožňující jen omezenou „filosofii pěti smyslů“ a omezující „životní energii“.

Takové programové odmítání vědy jako vrcholu lidského intelektuálního snažení nebylo pro další vývoj vztahů vědy a umění ještě tak škodlivé – předpokládalo dialog. Je-li věda „ďáblem, jehož veleknězem je Newton“, je stále faustovským ďáblem, „jenž dráždě k činnosti, jsa ďáblem, musí tvořit“. Nešťastnější bylo, že věda dostala nálepku suchopárnosti a nudnosti:

Vědo! Jsi věrnou dcerou starých časů! Tvůj zrak vše mění, pátravý a hbitý! Proč srdce rveš, jímž básník vzývá krásu, ty supe s křídly nudné reality? Jak tě mám ctít a za moudrou tě mít, když mu jen bráníš v jeho putování z klenotnic nebes poklad odhalit, ač vznáší se na křídlech odhodlání? Což Dianu jsi z vozu nevyštvala? A dryády jsi nevyhnala z háje, aby jim jiná hvězda sídlo dala? Nezaplašilas řekám zástup vil, trávám houf elfů, mně sen plný ráje, jejž jsem pod letním tamaryškem snil?

(E. A. Poe, Sonet – vědě, přel. J. Hiršal)

(V překladu jsme změnili ve verši „ty supe s křídly drsné reality“ slovo „drsné“ na „nudné“, což lépe odpovídá anglickému originálu „dull realities“.)

Může nás trochu překvapit, že autorem je právě Poe; každopádně však sonet vystihuje rozšířený pocit z vědy, a fyzika v tomto obecném povědomí zaujímá čelné místo, jako protipólu krásna, ztělesněného poezií. Tento pocit přežívá do značné míry dodnes, pokud dokonce nezesílil.

Přímý i nepřímý vliv vědy na umění ovšem trval. Znovu se ozývají nadšené výkřiky v osvícenském duchu, jakými jsou třeba „Písně kosmické“ nebo Nezvalův „Edison“. A je jistě něco podstatně jiného psát o skřítcích a opravdu na ně věřit, a něco jiného je se do víry ve skřítky stylizovat. Píše-li básník o hvězdách jako o dírách v obloze, je poetický účin obratu umožněn právě tím, že čtenář ví alespoň matně, co to hvězdy opravdu jsou.

V období „vědecko-technické revoluce“ přispěla k romantické nedůvěře k fyzice další skutečnost. Fyzika 19. století byla převážně akademickou záležitostí. V našem století přinesla záplavu aplikací, což vedlo k tomu, že fyzika je často v představě veřejnosti pokládána právě jen za základ technických oborů. A i když nejdeme tak daleko jako Snow, který nazývá literáty „přirozenými luddity“, rozbíječi strojů z počátku devatenáctého století – bylo to jistě nespravedlivé k poměrně velké tradici civilizační poezie v naší literatuře, či Karlu Čapkovi –, budeme asi souhlasit, že to přispívá k nesprávné představě, jaký je vědcův názor na svět. Cituji z jinak velmi pěkné knížky K. Sýse a J. Žáčka /5/: „Chtěl jsem pouze připojit, že z opojení vědecko-technickými zázraky, z něhož se zrodila velkolepá Nezvalova óda na tvůrčí aktivitu (míněn Edison), člověk sklonku století vystřízlivěl a že přes všechny geniální vynálezy je pořád největším zázrakem narození dítěte.“

Nechci nyní podkládat autorům názory, které neměli na mysli, domnívám se ale, že v obecném povědomí často panuje představa, že fyzik automaticky sdílí názor charakterizovaný jako „opojení vědecko-technickými zázraky“. Čteme-li úvahy velikánů moderní fyziky, nedávají tomuto názoru rozhodně za pravdu. Asi by neměli námitky proti označení narození dítěte za zázrak ve smyslu něčeho obdivuhodného, chápajíce, že autor citátu má na mysli nejen biologický fakt, ale i citové vztahy, které k němu vedly. Spíše by mohli mít námitky proti slovu „pořád“, jako kdyby se mohlo něco stát, co by náš obdiv snížilo, jako kdyby hlubší poznání zákonitostí přírody mohlo vést ke snížení známky „za umělecký dojem“. Nedomnívám se, že bychom například my, jak zde sedíme, byli méně okouzleni noční oblohou jen proto, že o hvězdách víme více, než je průměr. Abychom parafrázovali známý Einsteinův výrok, vesmír není méně obdivuhodný proto, že je pochopitelný.

Přímé reakce či alespoň proklamace reakcí na moderní fyziku najdeme na počátku našeho století v umění výtvarném, kde se hlásily ke slovu velice dravé modernistické směry. „Kubisté bez nějakých zvláštních znalostí Einsteinových teorií dávali tvar novému pojetí prostoru a času, které je s nimi spojeno.“ (N. Lynton /6/.) Zde je třeba klást důraz na slova „bez zvláštních znalostí“. Ve skutečnosti se vliv uplatňoval asi jen tak, že tito umělci měli určitou představu, že prostor a čas teorie relativity má jiná vlastnosti, než známe z běžná zkušenosti. Ale i toto nejasná chápání bylo, zdá se, inspirativní.

V osmém bodu „Manifestu futurismu“, vydaného r. 1909 F. T. Marinettim, se říká: „Jsme na nejzazším mysu století. Proč se ohlížet zpět, když máme vyrazit tajemné dveře nemožného? Čas a prostor včera zemřely. Žijeme již v absolutnu, neboť jsme stvořili věčnou, všudypřítomnou rychlost.“ Žargon Manifestu se zdá svědčit o tom, že autor měl určitou představu o pojmech teorie relativity, o tom, že relativita prostoru a času nějak souvisí s rychlostí, a udiví nás rychlost reakce na jen čtyři roky starou Einsteinovu teorii; stěží ovšem můžeme přijmout zdůvodnění proklamované teze skutečným obsahem teorie. Tyto explicitní demonstrace však nejsou důležité, vliv byl asi zprostředkovanější. Moderní fyzika rozhodně vnesla do obecného povědomí, že kromě pozorovatelné skutečnosti existuje svět neviditelných radiových vln a složitý mikrosvět určující makroskopické vlastnosti těles. Jedním ze specifických rysů moderního umění je snaha hledat „vnitřní“ skutečnost, proniknout za vnější pohled na realitu, a fyzikální obraz světa, sebeneurčitěji chápaný, sehrál určitě svou roli při formování těchto programů.

Přesto ale je asi pravdou, že to, čím teorie relativity, díky veliké popularitě Einsteinovy osobnosti známá alespoň podle jména, a méně známá kvantová teorie obohatily naše nazírání na svět, do obecného povědomí stále ani zdaleka neproniklo. Přitom nejdůležitější lekce, kterou nám moderní fyzika dala, že chceme-li se vyhnout logickým kontraverzím, musíme velice přesně formulovat otázky, které klademe, a definovat pojmy, jichž užíváme, svým významem přesahuje samotný obsah fyziky.

II. Fyzika .jako jedno z krásných umění

„Pánové, měl jsem tu čest být vybrán vaším výborem k obtížnému úkolu, proslovit přednášku o vraždě, jako jednom z krásných umění.“ Těmito slovy začíná přednáška Společnosti znalců vraždy v eseji Thomase De Quincey (1785 – 1859) „On murder considered as one of fine arts“. Ke splnění svého úkolu potřeboval přednášející užít samozřejmě určité dávky demagogie; domnívám se, že k tomu, abychom podobnou tezi prokázali o fyzice, budeme potřebovat demagogie daleko méně. Náš úkol je usnadněn i zároveň komplikován skutečností, že asi zcela vyčerpávající definice umění neexistuje. Existuje však řada dílcích kritérií uměleckého díla; pokusme se zjistit, jak fyzika obstojí, pokusíme-li se tato kritéria na ni užít či hovořit o ní v uměleckém žargonu.

Podle jedné charakteristiky umění hovoří především k emocím, zatímco věda je záležitostí racionální. Uveďme, co říká L. I. Bredvold v předmluvě k výboru básní A. Popea /8/ k problému intelektuálního verše v období anglického klasicismu: „Teoretickým problémem je, zda takový verš je skutečnou poezií. Někdy slyšíme, že ,intelektuální poezie‘ je rozporem v pojmech, protože poezie tak jako jiná umění je .jazykem emocí‘ . Nejlepším způsobem, jak takové vymezení vyzkoušet, je užít jej. Ilustrujme poněkud náhodně: Okamžitě by vyloučilo většinu řeckého sochařství, mnoho Bachovy hudby, mnohé obdivované pasáže Shakespeara a Browninga, umění Whistlerovo, většinu architektury a mnoho nezbytných předmětů užitého umění, které krášlí naše domácnosti. Je zřejmé, že tato teorie musí být chybná.“

Jako jiná specifika umění se uvádí, že je založeno na subjektivním zážitku tvůrce, zatímco věda popisuje objektivní skutečnost. Mohli bychom samozřejmě argumentovat realistickým uměním, ale i v jeho případě asi i odpůrce namítne, že subjektivní prvek tvůrce hraje tu rozhodující roli, která odlišuje umělecké dílo od pouhého popisu či faktograficky pojatého náčrtu. Ošidnou otázku „objektivního“ a „subjektivního“ v umění hluboce rozebírá A. Mercier /9/. Já zde užiji prostšího argumentu z hlediska spotřebitele umění.

Ať bylo dílo vytvořeno na základě jakkoli subjektivního prožitku, málokterý umělec touží po tom, aby zůstalo jen jeho soukromou záležitostí – chce mít posluchače, čtenáře, diváky. Komunikace uměleckého díla předpokládá, že vyvolá emoce v jeho spotřebiteli, a z hlediska konzumenta je tak trochu jedno, jak dílo vzniklo. A každý z nás ví, že fyzika umí působit i vysoce emotivně. Chápeme, že pro fyzika má dobrý smysl říct, že nějaká teorie je krásná, přičemž při podrobnější analýze, co tím míní, bude mít obtíže. Budou zde hrát určitě roli slova jako jednoduchost, symetrie,obecnost, dokonce možná i správnost teorie; přesné vysvětlení, proč užil slova „krásná“, však nebude o mnoho lehčí, než zdůvodnit, proč je krásná Venuše mé1ská, Kandinského obraz nebo Umění fugy.

Přicházíme k další otázce, otázce inspirace. Zde nebude pochyb, že inspirace hraje roli jak v umění, tak ve fyzice, otázka spíše zní, jaký je rozdíl mezi inspirací umělce a vědce, jakým způsobem je inspirace zpracovávána, kdo ji potřebuje ve větší míře. Když jsem citoval Poeův „antivědecký“ sonet, projevil jsem podiv, že jej napsal právě on. Vědě vyčítá nudnost právě tvůrce, který nechává uniknout zajatce Maelstrómu pomocí hydrodynamického triku, zakladatel logické detektivky, jenž nás udrží v napětí při mnohostránkovém rozboru postupu dešifrování pirátské listiny ve „Zlatém chrobákovi“, který může sloužit jako dokonalý příměr napětí z vědecké práce. To jsem však trochu odbočil; Poea chci nyní vzpomenout jako autora „Filosofie básnické skladby“ /10/, ve které minimalizuje podíl inspirace při své básnické tvorbě. Uvádí: „Spisovatelé, zvláště básnící, nás většinou chtějí udržovat v domnění, že tvoří v jakémsi ušlechtilém šílenství, v jakémsi nazíravém vytržení, a přímo by se zhrozili, kdyby měli dát čtenáři nahlédnout za kulisy... co se mne týče, nelibuji si v onom zdráhání a dovedu se kdykoli bez nesnází rozpomenout na postup kterékoli své skladby. Vybírám si Havrana, protože je nejznámější. Hodlám prokázat, že skladba nevděčí na žádném místě náhodě nebo intuici, že celé dílo pokračovalo až k závěru s přesností a neúchylností početního úkolu.“ A téměř jako parafráze analýzy ve Zlatém chrobákovi následuje výklad racionální syntézy „Havrana“: „... A tak jsem připadl na to, že nejlepším refrénem bude jediné slovo ... musí být zvučné a musí se dát zdůraznit prodloužením ... úvahy vedly k nejplnozvučnější samohlásce dlouhému o, spojenému se souhláskou r, kterou lze nejvíce protáhnout ... bylo nemožné přehlédnout slovo ,nevermore‘ ... bylo třeba záminky pro neustálé užívání slova ... nabízel se papoušek, kterého vzápětí vytlačil havran, který neskonale více odpovídal zamýšlenému tónu ... který ze smutných námětů je nejsmutnější? ... smrt ... a kdy nejbásničtější ... těsně spjatá s krásou, nejlépe se hodí ústa osiřelého milence.“ A rozbor pokračuje, až vyčerpá všechny detaily básně. Je jistě třeba mít na paměti slova I. Hurníka z jeho rozboru umělecké inspirace /1/: „A tak nezbývá, než brát výroky umělců o genezi jejich děl s rezervou – navíc z jednoho důvodu: jakmile autor vezme pero do ruky, aby psal o svém díle, stává se z něho příležitostný literát. Jme se tvořit, stylizovat se.“ Nicméně i když vezmeme Poeův esej jako zpětnou konstrukci, je velice přesvědčivý a jen málo fyziků by asi dokázalo tak přesně zdůvodnit jednotlivé kroky, které vedly ke konečnému výsledku. Každopádně učebnicové postupy induktivního budování teorií bývají obdobnými zpětnými konstrukcemi. Při výkladu teorie relativity bývá základním kamenem Michelsonův pokus, který Einstein prý neznal. Nebo vzpomeňme kvantovou mechaniku, kde byla dříve známa Schrödingerova rovnice, než interpretace vlnové funkce. Historky o Paulim, kterého napadl vylučovací princip při pohledu na přeskupování tanečnic v jakési revue, nebo o Feynmanovi, který prý v soudním procesu proti striptýzovému podniku uváděl v jeho prospěch, že nejlepší myšlenky ho napadly právě tam, jsou sice anekdotické, ale dobře se řadí k historce o Brucknerovi, kterému Wagner ve snu nadiktoval téma, a dalším historkám o inspiraci umělců.

Nyní nám však odpůrce namítne, že i když jsme obratnou sofistikou dosáhli v naší argumentaci některých dílčích úspěchů, zcela selžeme ve věci nejpodstatnější. Umělec má k dosažení svého záměru volnost ve volbě výrazových prostředků, kdežto fyzik jen zapisuje sdělení diktovaná přírodou do stereotypní řeči matematiky.

Matematika je jistě jazykem neobvyklým a získání estetického zážitku z díla v něm napsaného vyžaduje značné předběžné znalosti. Okruh konzumentů, kteří se mohou s uměleckými díly z ateliéru fyziky seznamovat přímo a ne zprostředkovaně, je tedy dosti omezen. Ale umění má velikou tradici a obratnost ve vyvracení nařčení z nesrozumitelnosti. Zůstaneme-li jen na poli literatury, některé básně citovaného W. Blakea nelze dobře číst bez slovníku jeho symboliky. J. Joyce prý prohlásil v odpovědi na kritiku, že vytváří nová slova – Finnegan's Wake, odkud pochází slovo „quark“, představuje extrém, kde je již běžná angličtina v menšině – a tím činí své dílo nesrozumitelným: „Naučil jsem se norsky, abych mohl číst Ibsena v originále. Proč by se lidé nemohli naučit mému jazyku, aby mohli číst mne?“ A výrazové prostředky moderního umění výtvarného či hudby kladou často na spotřebitele též značné nároky. Zde by tedy neměla být závada.

Odpůrce ovšem namítne, že stále uhýbám od toho podstatného – kde je ve fyzice tvůrčí volnost v užívání jejího jazyka?

I zde se dá úspěšně oponovat. Newtonovy zákony ve tvaru diferenciálních rovnic, Lagrangeovy rovnice druhého druhu, Hamiltonovy kanonické rovnice jakož i plejáda diferenciálních a integrálních principů mechaniky jsou do značné míry různým formálním vyjádřením téhož. Fyzikální teorie se spíše vytváří, než objevuje. Samozřejmě, že fyzik nemá ve vyjadřování naprostou volnost, ale tu nemá ani umělec. Více, než třeba přiznává,je svazován konvencí a módou, nechce-li zůstat zcela bez ohlasu. Formální výboje ve fyzice nejsou samozřejmě samoúčelné a nejsou diktovány jen estetickými požadavky, je v nich snaha o lepší porozumění problému, lepší zvládnutí techniky řešení, vytvoření základu pro hledání konstruktivní cesty dále. Ale podobná argumentace se objevuje i v obhajobách formálních výbojů v umění.

Mohl bych pokračovat v rozvíjení analogií, např. mezi úlohou modelu ve fyzice a tím, co se nazývá uměním zkratky. Ale už bych asi unavoval a krom toho mne asi podezříváte, že to všechno nemyslím úplně vážně. Opravdu, snažil jsem se užít osvědčeného literárního triku, nadsázky, abych ukázal na styčné body mezi duchem fyziky a umění; s jakým úspěchem, musíte posoudit vy.

III. Jak stavět mosty

Zaměření tohoto semináře je pedagogické, proto uvedu několik námětů, jak stavět ne-li mosty, tedy alespoň lávky přes uvedenou trhlinu, pokud se domníváme, že to stojí za to.

(a) Student se většinou učí fyziku jako souhrn hotových faktů. Méně už získává představu, jak fyzika vzniká, jaký je tvůrčí proces fyziky. I to je možná jednou z příčin, proč mu fyzika připadá suchopárná. Na semináři věnovaném výuce českého jazyka by se možná ozývalo obdobné lamentování, že výuka literatury vede spíše k učení se faktů o spisovatelích, než k tomu, aby se žák naučil číst knížky a mít je rád. V obojím případě nemohou problém řešit učebnice, ale osobnost učitele.

(b) „Jan Neruda byl velikým básníkem století páry.“
- „Století páry?“
- „Ano, 19. století se nazývá stoletím páry. To jsme se učili ve fyzice.“
- „No jo, ve fyzice. Ale my budeme užívat zavedeného názvu 19. století.“

(volně podle filmu Marečku, podejte mi pero)

Zde je vystižen problém snad všech předmětů ve školní výuce, že návaznost jednotlivých předmětů je velmi malá. Z hlediska uvažovaných otázek není v našich silách ovlivnit, aby se při výkladu „Kosmických písní“ mluvilo o Leverrierovi a Adamsovi, i když by to podle mého názoru prospělo k lepšímu pochopení ducha Nerudova díla. Ale můžeme ovlivnit, aby se při výkladu o planetách mluvilo o Nerudovi a Arbesově „Ethiopské lilií“, případně i Faustovi a sci-fi, v akustice o fyzikálním základu hudby apod, Domnívám se, že prospěch by byl oboustranný.

(c) Neměl by vznikat dojem, že fyzika představuje jen podklad aplikací. Řečeno obrazněji, je samozřejmě dobré, když student pochopí, proč hraje tranzistorové rádio; bylo by též dobré, kdyby zároveň pochopil, že se tím i obecněji dovídá, jak chodí svět.

Děkuji Dr. Z. Horskému, CSc, a Doc. Dr. L. Pátému, CSc, za cenné připomínky.

Literatura

1. Kosmické rozhledy (1980) 55-69, 115-152.

2. Kosmické rozhledy (1983) 105-152.

3. Snow C. P.: The Two Cultures and The Second Look. Cambridge Univ. Press, Cambridge 1964.

4. Kline M.: Mathematics in Western Culture. Oxford Univ. Press, _vOxford, London, N. Y. 1971.

5. Sýs K. a Žáček J.: 1 + 1, Aneb nesoustavný rozhovor o poesii. Československý spisovatel, Praha 1986.

6. Lynton N.: Umění 19. a 20. století. Artia, Praha 1981.

7. Pijoan J.: Dějiny umění 9. Odeon, Praha 1983.

8. Selected poems of A. Pope, ed. L. I. Bredvold. Crofts and Comp., New York 1933.

9. Mercier A.: Science and Art in Physical Reality and Mathemati-cal Description. Enz C. P. and Mehra J. ed. D. Reidel Publ. Comp., Dotrecht 1974. P. 3-22.

10. Poe E. A.: Filosofické básnické skladby. Olomouc 1932.

ERWIN SCHRÖDINGER A JEHO ROVNICE

Jiří Komrska

Ústav přístrojové techniky ČSAV 612 64 Brno, Královopolská 147

Autorský přepis magnetofonového záznamu přednášky (Dl/97-100, D4/283) proslovené 17. září 1986.

Vážené kolegyně, vážení kolegové,

nevzpomenuli jsme 25. výročí Schrödingerovy smrti, nevzpomenuli jsme, že uplynulo už šedesát let od doby, co byla zformulována Schrödingerova rovnice. Vzpomeňme tedy s jedenáctiměsíčním předstihem 100. výročí Schrödingerova narození a připomeňme si jeho životní osudy.

Schrödinger byl typem komorního vzdělance. Nebyl to jenom vědec, jenom učenec nebo jenom filosof. Byl to skutečně všestranný vzdělanec. Nikdy nepracoval v týmu. Jen asi devět z jeho zhruba 160 publikací má spoluautory. A jsou to publikace spíš drobnější. Pozornost, které byla věnována jeho osobě, byla nepoměrně menší ve srovnání s pozorností věnovanou ostatním tvůrcům moderní fyziky. Může to být způsobeno jeho odbornou opozicí ke kodaňské interpretaci kvantové mechaniky a mentální odlišností od ostatních odpůrců kodaňské interpretace. Schrödinger byl Evropan, který se necítil nucen ihned se veřejně vyjadřovat ke konfliktům na kontinentu a raději se tomu vyhýbal.

O podrobnostech Schrödingerova života není u nás dost původního materiálu. Přečetl jsem tedy větší množství Schrödingerových životopisů, vzpomínek, nekrologů apod. a stalo se, že jsem si vytvořil tolik různých portrétů, kolik bylo zdrojů. Zaměřil jsem se tedy na tyto nejvýznamnější: W. H. Elsasser je všeobecný fyzik, který pracoval v kvantové mechanice, jaderné fyzice, biofyzice, geofyzice, meteorologii, setkával se se Schrödingerem počátkem třicátých let v Berlíně a vyznal se v hlubinné psychoanalýze. Jeho vzpomínky /l/ obsahují mnoho pozoruhodného. Faktograficky je bohaté biografie od A. Hermanna /2/. Vynikající kniha Jammerova /3/ nedává příliš informací o Schrödingerově životě, neboť je zaměřena na historii kvantové mechaniky. Podobně stas Polákova /4/. Existuje však i Schrödingerova autobiografie /5/, Jenomže se mi zdá, že Schrödinger se v ní poněkud stylizoval a snažil se trochu zlehčit svůj význam i hloubku své osobnosti. Byl v tomto směru předchůdcem dnešních lidi: Naši pradědové, když šli do hospody, předstírali, že jdou do kostela, kdežto my, když jdeme do kostela, předstíráme, že jdeme do hospody.

Skutečně, literatura o Schrödingerovi není příliš bohatá. Navíc nejsou v našich knihovnách velká kompendia věnovaná historii kvantové mechaniky, která byla publikována v posledních dvaceti letech. Můžeme se však těšit, že za rok tomu bude jinak, protože celá řada institucí se připravuje na oslavy 100. výročí Schrödingerova narození. Konkrétně u nás se můžeme těšit na medailon z pera kol. R. Zajace a J. Šebesty v Pokrocích matematiky, fyziky a astronomie, na několik článků v Čs. čas. fyz. A a snad i na rakouské poštovní známky.

Jak tedy za této situace mám svou přednášku koncipovat? Obávám se, že pořadatelé ode mne očekávají slavnostní přednášku. Ale toho jednak nejsem schopen, jednak se mi zdá, že to teď ani nelze udělat. A tak mi dovolte, abych se zaměřil na faktografii a jenom občas si dovolil nějaký komentář.

Mnohé, co bylo na tomto semináři řečeno, se mi zdálo vhodné v souvislosti se Schrödingerem. Jenže člověk to zase zapomene. Jedno mne však upoutalo do té míry, že jsem to nezapomněl. Je to včerejší poznámka kol. L. Pátého, že při popularizaci by se mělo ukazovat, jak je to pracné, co to stojí námahy a v jistém smyslu i utrpení, než se něčeho dosáhne. A to mě vedlo k tomu, že jsem celou přednášku přeskládal. Zaměřím se na Schrödingerovo mládl a pokusím se naznačit, jak velký byl vklad – společenský, osobní i Schrödingerovy rodiny – nutný k tomu, aby se Schrödingerův talent mohl rozvinout.

Dětství

Schrödinger se narodil 12. 8. 1887 ve Vídni. Ve své nobelovské autobiografii /6/ charakterizuje Schrödinger tehdejší Vídeň jako „velmi veselé radostně živoucí město, které bylo hlavním mlatem dunajské monarchie“. Mnozí životopisci /l/ – a to se netýká jenom Schrödingera, ale také třeba Macha /7/ – líčí ty pro nás nešťastné Habsburky jako osvícené panovníky, kteří citlivě a moudře spravovali svůj mnohonárodnostní stát, ve kterém vzkvétaly všechny národy. Možná se jim to tak jeví ve srovnáni s hrůzami jinde ve světě. Mně však poněkud vadí, že neberou na vědomí, že to začalo hlavami na mostecké věži a skončilo na následky naprosté necitlivosti k tužbám slovanských národů. Ale nestavme se do opozice a věnujme se radostnějším věcem.

Schrödingerův otec, Rudolf Schrödinger, byla postava takřka renesanční. Jeho rod pocházel po mužské větvi z Falce, byl však již třetí či čtvrtou generaci usazen ve Vídni. Byl majitelem zděděné továrničky na voskované plátno vedené ve starém stylu, ala zajištující rodině přiměřenou existenci až do 1. světové války. Vystudoval chemii na vídeňské technice a jeho zájmy byly všestranné a hluboké. Zajímal se o italské malířství a sám byl aktivní v krajinomalbě a grafice. Od přelomu století se zabýval botanikou – experimentální morfogenetikou a fylogenetikou –, a to tak, že ho někteří životopisci jeho syna považují za botanika. (Tomuto omylu podlehl v krásné vzpomínce /8/ i pan profesor Brdička.) Měl také několik publikací v časopise c. k. zoologicko-botanické společnosti ve Vídni. Oženil se s dcerou svého profesora z techniky, chemika Alexandra Bauera, jehož manželka byla Angličanka. Schrödingerova matka bývá charakterizována /9/ jako velmi hodná, od přírody veáelá, nepraktická, ale současně nenáročná žena. Nepraktická? – ale zajistila, že Schrödinger od malička ovládal angličtinu, což se mu po celý život znamenitě hodilo.

Přes určitou osamělost jedináčka měl Schrödinger nádherné dětství, které mu budou moci závidět lidé i v mnohem rozvinutějších společnostech, než byla tam ta stará. Schrödinger byl „lieblingskind“ vychovávaný v rodině a rodinou. Do obecné školy nechodil vůbec – jen několik týdnů, když byl s rodiči na dovolené v Innsbrucku. Hlavním vychovatelem, přítelem, neúnavným „gesprächspartnerem“ i nejvyšší apelační instancí ve všech otázkách, které mohly malého Schrödingera zajímat, však byl otec.

V letech 1898 – 1906 studoval Schrödinger akademické gymnázium ve Vídni. Byl vynikajícím studentem a gymnázium bylo také vynikající: Během půl století na něm maturovaly osobnosti jako L. Boltzmann, T. Masaryk, S. Zweig, E. Schrödinger. A to jsou postavy na které jsem připadl více méně náhodou, když jsem se Schrödingerem zabýval. Málokteré gymnázium se může pochlubit něčím podobným. Důraz byl kladen na latinu a řečtinu. Exaktní vědy měly méně hodin, ale výuka byla vynikající. Schrödinger měl v oblibě všechny předměty – matematiku, fyziku, přísnou logiku gramatik klasických jazyků. Ošklivilo se mu biflováni „náhodných“ dat historických a biografických událostí. Měl velmi rád německé básníky a dramatiky, ale cítil odpor ke školským rozborům jejich děl.

Neodolám pokušení a přečtu nyní delší úryvek ze Schrödingerovy autobiografie, který atmosféru dětství a raného mládí autenticky vykresluje. Odpusťte, že to budu číst nepěkně. Není to způsobeno jenom tím, že neumím číst, ale také tím, že Schrödinger používá dlouhých a velmi členitých vět /5/, str. 23-26:

„„Moje dětství a mládí (1887 až asi 1910 a déle) bylo především pod otcovým vlivem, nikoli úmyslně pedagogickým, ale přirozeným. To bylo zaručeno především tím, že on byl poměrně mnoho doma, více než většina mužů, kteří jsou v zaměstnání, a potom také tím, že také já jsem pobýval hodně doma. Základní vyučovací hodiny mně dával učitel obecné školy, který ke mně přicházel myslím dvakrát týdně, a v gymnáziu byl tenkrát ještě zdravý mrav, že se vystačilo 8 pětadvaceti hodinami týdně dopoledne (jen na hodinách protestantského náboženství jsem se musel objevit dvakrát týdně odpoledne – a hodně jsem se tam naučil, i když ne především náboženství). Uměřenost školního vyučování, co se týká času, má velké výhody; gymnazistovi zůstává, když mu na tom záleží, čas k přemýšlení a na soukromé hodiny, například moderních jazyků, deskriptivnl geometrie, o což se gymnázium s humanitním zaměřením nestará. Mohu svou tehdejší školu (Akademické gymnázium) velice pochválit. Skoro nikdy jsem se nenudil, a v řídkých případech, kdy tomu tak bylo (filozofická propedeutika, velmi špatná výuka), jsem vypnul pozornost a dělal francouzský překlad.

K tomu ještě všeobecnou poznámku. Od objevu, jak funguje dědičnost daná chromozómy, se leckdo snaží přehlížet stejně důležitý a mnohem déle známý dědičný vklad daný sdělenými myšlenkami, výchovou, tradicí – není prý tak důležitý, protože není dědičně stálý. To poslední je pravda. Nicméně je známo na jedné straně ze smutného případu Kaspara Hausera*, na druhé straně z případu skupiny divochů z Tasmánie patřících ještě době kamenné, kteří zasazeni do anglického prostředí prošli „prvotřídní“ anglickou výchovou, přičemž dosáhli standardu vzdělání mladých Britů „z lepší rodiny“, že lidé jako my vznikají společným působením chromozómového kódu a kulturního lidského okolí. Duchovní úroveň každého jednotlivce je produktem „nature“ (přirozeného základu) a „nurture“ (výchovy). Tato úvaha vede každého rozumného člověka k tomu, že uznává nesmírnou důležitost školy (na kterou je třeba pohlížet ne jako na politikum, jak to chtěla císařovna Marie Terezie, ale jako na humanum). Že však chromozómy a škola ještě nejsou všecko, ale že k tomu patří i domácí prostředí, aby připravilo půdu pro setbu, kterou má škola zasévat, a učinilo ji úrodnou, to zdá se nevědí nejen ti, kdo chtějí na vysoké školy povolit přístup jen dětem z rodin s nízkou úrovní vzdělání (ptáme se: budou jejich děti potom snad opět ze vzdělání vyloučeny?) – ale dokonce instituce vysoce vzdělaného Spojeného království vytrhují dítě z rodiny, a to tím dříve, čím je rodina vznešenější (ba i malého následníka trůnu odvedla vůle národa jeho matky, Alžběty II., takřka násilím do takového elitního ústavu).

Ale to všechno se mne netýká. Podnět k této poznámce mně dalo vědomí, za jak neslýchané mnoho děkuji neustálému pobytu se svým otcem během svého dospívání, o co méně bych byl měl ze školy bez něho. Už jen to, že věděl o všech věcech, které se tam vyskytovaly, a o mnohém jiném, co s nimi souviselo, že je nemusel asi tak před třiceti léty jenom nabiflovat, ale že ho také ještě dnes zajímaly! Bylo by únavné vypočítávat podrobnosti.““

*) Kaspar Hauser (kol. 1812 - 1833), pověstný německý nalezenec, vychovaný od r. 1828 v Norimberku a zemřelý patrně následkem vlastního poranění dýkou. Přičítán mu původ ze vznešené rodiny. ...V krásné literatuře častěji použit. ... (Masarykův slovník naučný, 1927)

Vídeňská univerzita

Na univerzitu vstoupil Schrödinger v r. 1906. Vídeňská univerzita byla jediná, na které studoval, což považoval za anomálii ve srovnání s německými kolegy. Nicméně ta vídeňská univerzita byla opět skvělá. Bohužel, rok 1906 je rokem Boltzmannovy sebevraždy, ale Boltzmannův duch ještě dlouho univerzitu ovládal.

Když se řekne Boltzmann, představí si člověk Vídeňáka. Proto mne překvapilo, že většinu svých objevů vykonal Boltzmann ve Štýrském Hradci: Ergodická hypotéza, statistický charakter 2. věty termodynamické, dokonce i teoretické zdůvodnění Stefanova-Boltzmannova zákona, to všechno bylo vykonáno ve Štýrském Hradci. To je významné v souvislosti se Schrödingerem, neboť to částečně vysvětluje, proč dal v r. 1936 přednost katedře ve štýrském Hradci před působením na britských univerzitách. Z fólie je také zřejmé, jak mocně přitahovala Boltzmanna Vídeň.

Boltzmann se nám dnes jeví jako člověk, který byl uštván odpůrci atomové hypotézy. A hodně na tom je. Ale Boltzmann byl také samorostlou a uznávanou vedoucí osobností tehdejší evropské fyziky. Svědčí o tom i skutečnost, že mu bylo v r. 1889 nabízeno místo po Kirchhoffoví v Berlíně, které nepřijal („... jemu, jenž miloval jistou svobodu, nemohlo se v Berlínu líbiti. Bylo mu tam naznačeno velmi směrodatnou (ženskou) osobností, že se neumí náležitě chovati u stolu.“ P. Lenard).

Všimněme si také oborů, ve kterých Boltzmann pracoval, a porovnejme je s obory, v nichž později pracoval Schrödinger. Je z toho vidět velmi významný vliv univerzitního prostředí na Schrodingera. A v tomto duchu bych ještě chvíli rád pokračoval.

Schrödingerovi univerzitní učitelé byli skvělí: Experimentální fyziku studoval u Franze Exnera. (Není to onen pražský filozof téhož jména, jenž oponoval Hegelově dialektice, ale experimentální fysik a Röntgenův spolužák na technice v Curychu.) Data jeho života i obory, jimiž se zabýval, jsou uvedeny na průsvitce. Zjistil mimo jiné, že index lomu plynného prostředí závisí na hustotě plynu, Že čtverec rychlosti částic při Brownově pohybu je úměrný absolutní teplotě, a položil základy moderní teorie atmosférické elektřiny.

Teoretickou fyziku studoval Schrödinger u ještě výraznější osobnosti. Byl to Boltzmannův žák a nástupce Friedrich Hasenöhrl. Jeho osud byl nešťastný, padl poměrně mlád v 1. světové válce. Když Schrödinger vstupoval na univerzitu, měl Hasenöhrl vstupní přednášku o Boltzmannově životním díle, která na Schrödingera mocně zapůsobila. Hasenöhrl byla osobnost mnohem významnější, než jak to odpovídá dnešnímu povědomí. V r. 1904, rok před Einsteinem, našel vztah se zi energií a hmotností tepelného záření v dutině ve tvaru E = 4/3 m c² . Když se pak Němci za Hitlerovy doby snažili Einsteina jako neárijce eliminovat, připisovali prioritu vztahu mezi energií a setrvačnou hmotností Hasenöhrlovi. Ale Hasenöhrl za to nemohl, neboť byl již dávno mrtev. Hasenöhrlův rozsáhlý kurs teoretické fyziky (4 roky, 5 hodin týdně) měl na Schrödingera hluboký vliv. Jeho prostřednictvím se Schrödinger seznamoval se současnou teoretickou mechanikou, s problémy vlastních hodnot v mechanice kontinua atd., neboť mu „bylo vždy zatěžko studovat pouze z knih“. Tento kurs byl vzorem i základem pozdějších Schrödingerových brilantních přednášek ve Stuttgartu, Curychu a Berlíně, jak o tom ještě bude řeč. Prostě Hasenöhrl byl člověk, který měl vedle otce na Schrödingera největší vliv, a Schrödinger ho často vděčně vzpomínal. Také ve své nobelovské autobiografii /6/: „Vnitřní hlas mi říká, že kdyby Hasenöhrl nebyl padl, jeho jméno by dnes znělo místo mého.“

Erwin Schrödinger

Ludwig Boltzmann a Friedrich Hasenöhrl

Matematiku na univerzitě studoval u Wirtingera, geometrii u Kohna, chemii u Z. H. Skraupa (synovec F. Škroupa), filosofii u W. Jerusalema a vše přijímal s vděčností a úctou.

V r. 1910 Schrödinger promoval u Hasenöhrla a od roku 1911 až do vypuknutí války byl asistentem na experimentální fyzice u Franze Exnera. Schrödinger musel vykonat celé praktikum a rád se zabýval některými přístroji, zejména optickými. Komentoval to takto /5/, str. 17: „Tak náležím k teoretikům, kteří z přímé zkušenosti vědí, co znamená měřit. Zdá se mi, že by bylo lepší, kdyby jich bylo víc.“ V té době se také zabýval – pod vedením Egona von Schweidlera, tehdy soukromého docenta na katedře F. Exnera – měřením radioaktivity atmosféry a měřením radioaktivity vůbec. (Tento obor byl rovněž na vídeňské univerzitě velice rozpracován.) Z tohoto předválečného období pochází celkem 12 publikací, a překvapuje, že Schrödinger hodnotí toto období dosti kriticky /5/, str. 16: „V těchto dobách jsem si uvědomil dvě věci: Za prvé, že se nehodím na experimentátora. Za druhé, že půda, na které jsem žil, a lidé, se kterými jsem tam žil, už nejsou způsobilými dosáhnout experimentálního pokroku velkorysým způsobem. Vězelo to mezi jiným v tom, že zlaté vídeňské srdce dosazovalo roztomilé packaly (často podle principu služebního stáří) na klíčová místa, kde brzdili činnost, zatímco by zde bývalo bylo zapotřebí skutečných osobností, i kdyby musely být získány zdaleka. Tak nám byla vzata z rukou elektřina ovzduší a radioaktivita, které ve skutečnosti vznikly ve Vídni, a kdo se cítil povolán se jimi vážně zabývat, musel jít za nimi z Vídně do Berlína, jako například Lise Meitnerová.“

První světová válka

Vypukla 1. světová válka a Schrödinger byl 31. 7. 1914 povolán do armády. Otec mu koupil dva revolvery a Schrödinger později vyjadřuje svou radost nad tím, že jich nikdy nepoužil ani proti člověku ani proti zvířeti. Schrödinger byl příliš mlád, aby mělo smysl, aby se k válce vyjadřoval, ale z jeho pozdějších formulací je zřejmé, že smýšlel jako Evropan, stejně jako E. Mach nebo papež Pius X. Považoval válku za nesmysl a zločin. Jeho stanovisko se velmi liší od stanoviska říšsko-německých vědců – i takového Plancka, Laueho, Rontgena aj. – , kteří podepsali nebo aspoň schvalovali provolání německých intelektuálů, kteří obhajovali porušení mezinárodního práva, k němuž došlo vstupem německých vojsk do neutrální Belgie,a někteří (Planck, Laue) setrvávali v těchto názorech ještě dlouho po válce /10, 11/. O tomto mluvím ne abych je hanil, neboť si těchto lidí nesmírně vážím, ale abych ukázal rozdíl mezi Schrödingerem a jimi a také na jejich vlastní velikost, když přes tyto odlišné názory pak (v r. 1927) Schrödingera zvali a vzali do Berlína (nemluvě o přijetí Einsteina, který už v době vypuknutí války v Berlíně byl).

Schrödinger dělal důstojníka u nějakých dělostřeleckých útvarů a později u meteorologické služby. Vyjadřuje se o tom dosti posměšně /5/, str. 32: „O válce: Po dlouhém povalování na Predilském sedle, ve Františkově pevnosti, u Kremže a Komorn, po krátké službě na frontě s malým oddílem a s jedním směšným lodním dělem u Gorizie a pak u Duina jsme byli staženi nejprve do blízkosti Sistiany; pak jsem přišel s ještě směšnějším lodním dělem do nanejvýš nudného, ale krásného záložního postavení u Prosecca, asi tři sta metrů nad Terstem. Tam mě jednou navštívila moje budoucí žena Annemarie. Jednou přijel bratr naší císařovny Zity, princ Sixtus von Bourbon, a přehlížel naše postavení. Byl v civilu. Jak jsem se teprve později dozvěděl, byl tehdy nepřátelským důstojníkem v belgické armádě; to z toho důvodu, že ve Francii je zakázáno zákonem, aby kdokoli z Bourbonů vstoupil do armády. Jeho pobyt v monarchii se týkal uzavření separátního míru mezi Rakousko-Uherskem a Dohodou, tedy záludná zrada Německa, která se však bohužel neuskutečnila.“

Na rozdíl od L. de Broglieho, který byl v té době plně vytížen jako telegrafista na Eiffelově věži a k vědecké práci se vůbec nedostal, Schrödinger měl možnost se jen tak poflakovat, pozorovat zajímavé přírodní úkazy a sledovat vývoj fyziky. Studoval i Einsteinovy články o obecné relativitě a mohl také sedm článků opublikovat.

Poválečné období 1918 – 1921

Válka končila a tím, že Hasenöhrl padl, docházelo k přesunům na katedrách teoretické fysiky. Schrödinger měl povolání za mimořádného profesora do Černovců. Měl přednášet teoretickou fyziku, ale těěil se, že se bude zabývat filosofií. Ale válka skončila, Černovcy připadly Rumunsku a dvaatřicetiletý Schrödinger zůstal bez existenčního zajištění ve vyhladovělé Vídni. Nepřestal však pracovat, oženil se, a začátkem dubna 1920 odešel na slušně placené místo do Jeny, kde přednášel a působil jako „Haustheoretiker“ u Maxe Wiena. Pobyl tam vsak jen 4 měsíce a dostal povolání za mimořádného profeaora na techniku do Stuttgartu. Tam působil pouze jediný semestr s dostal povolání za řádného profesora do Kielu, Vratislavi a Vídně. Schrödinger by se byl ovšem nejraději stal Hasenöhrlovým nástupcem na universitě ve Vídni. Jenže poměry tehdy (1920/1921) byly ve Vídni tak neutěšené, že dal přednost Vratislavi.

Už ve Stuttgartu slyšel Schrödingerovy znamenité přednášky profesor Speiser z Curychu, a tak se stalo, že Schrödinger dostal také nabídku řádného profeaora na universitě v Curychu. Schrödinger tedy působil ve Vratislavi jen několik týdnů a stal se nástupcem Einsteinovým, Laueovým a Debyeovým na univerzitě v Curychu. Na technice v Curychu působili v téže době Herman Weyl a Peter Debye, a tak se v roce 1921 34-letý Schrödinger konečně usazuje.

Teď si dovolím přečíst kousek ze Schrödingerovy autobiografie, který obsahuje jakousi Schrödingerovu zpověd a ukazuje, co musel Schrödinger zaplatit za své odborné i lidské prosazeni. Těsně po válce totiž onemocněl Schrödingerovi otec. Ve Vídni byl tehdy obhospodařován svítiplyn a Schrödingerovi se rozhodli svítit karbidovými lampami, které opatroval nemocný Schrödingerův otec. /5/, str. 20 až 27:

""Vznikal odporný zápach, který se neomezil jen na jeho krásnou knihovnu, která byla nyní prohlášena za karbidovou laboratoř a ve které před dvaceti lety, když se učil u Schmutzera dělat rytiny, leptal své měděné a zinkové desky v kyselinách a chlorovodíku, což bylo tenkrát předmětem velkého zájmu jeho syna, gymnazisty. Ten ho teď v tom nechal lítat a byl šťasten, že po téměř čtyřleté válečné přestávce může opět trávit svůj čas v milovaném fyzikálním ústavu. Mimoto se na podzim 1919 zasnoubil s tou, která je nyní (1960) už čtyřicet let jeho ženou.

Zda měl můj otec dostatečnou lékařskou a pečovatelskou pomoc, nevím – ale že jsem se o to velmi málo staral, to vím: jak to teď vidím, měl jsem jít k Richardu von Wettsteinovi a poprosit ho, aby zainteresoval některého kolegu z jiné fakulty na osudu muže, kterého mohl pokládat vždy za svého přítele. Byla by mohla lepší rada zabránit rychlému chátráni způsobenému arteriosklerózou? A když ano, bylo by to bývalo pro nemocného lepší? Po zrušení skladu a voskovaným plátnem a linoleem na Štěpánském náměstí (1917 pro nedostatek zboží) jsme byli vlastně v těžké peněžní tísni, jejíž rozsah znal úplně jen on. Zemřel o štědrém večeru 1919 klidně v dědečkově křesle. Další rok přinesl úplnou inflaci, znehodnotil jeho bankovní konto, které bylo beztoho příliš malé, aby mohli s matkou slušně žít, znehodnotil výtěžek z jím prodaných (s mým souhlasem!) peršanů, rovněž tak výtěžek z přístrojů (tří mikroskopů a jednoho mikrotomu) prodaných pod cenou po jeho smrti (s jeho svolením) a stejně tak pakatel, za který šla do antikvariátu větší, pro mne méně zajímavá část jeho knihovny. Velkou starosti jeho posledních měsíců bylo to, že jsem si ve svých dvaatřiceti letech prakticky nic nevydělával – tisíc korun za rok brutto, neboť je určitě (mimo mých čtyř důstojnických let) začlenil do svého přiznáni daně z přijmu a platil z nich. Jediným „úspěchem“ jeho synáčka, o kterém se ještě dověděl, bylo, Že jsem obdržel nabídku na lépe placené asistentské místo a  povinností přednášet jako soukromý docent u Maxe Wiena v Jeně – kam jsem odešel na začátku dubna 1920 se svou mladou ženou, zanechávaje neslavně matku poněkud na holičkách. Ta se trápila s vyklízením a balením, protože – všichni jsme byli vskutku raněni slepotou – její otec, kterému patřil dům, měl velkou starost o to, od koho bude dostávat po otcově smrti nájem z bytu. Od nás ne, a tak musela vdova ven, kam vlastně, ani nevím, ustoupit nájemníku schopnému víc platit, kterého obstaral laskavě můj tchán in spe v podobě bohatého věčného Žida. Jak bylo řečeno, byli jsme všichni raněni slepotou. neboť, jak bylo později z mnoha podobných případů patrno, byl by býval tento velký, dobře zařízený byt pro mou matku zdrojem příjmů, kdyby byla žila déle než do podzimu 1921 (metastáza v páteři po karcinomu prsu údajně radikálně operovaném 1917). Jen zřídka si pamatuji sny a velmi zřídka (snad mimo v nejranějším dětství) se mi zdají zlé sny. Po otcově smrti a ještě dost dlouho potom přicházíval, i když s určitými rozdíly, tento úzkostný sen: můj otec je ještě naživu a já přece vím, že jsem zašantročil všechny jeho krásné přístroje a dal pryč knihy, zejména botanické. Proboha, co teď bude dělat, když jsem lehkovážně rozmetal základy jeho duševního života, nenávratně! – Mám za to, že tento úzkostný sen byl způsoben špatným svědomím z mého málo chvalitebného chováni vůči rodičům v létech 1919 – 1921. S tímto výkladem je v souladu, že jinak jsem tíživých snů ušetřen, protože si totiž velmi zřídka, jak se říká, „dělám z něčeho svědomí“.""

Inu, „... obviňuje-li nás naše svědomí, je Bůh větší než naše svědomí a ví všecko“ (1J3,20). Schrödinger však – jak se zdá – nenašel v láskyplné Boží vševědoucnosti útěchu a těmito výčitkami dlouho trpěl.

Profesorem na univerzitě v Curychu a Schrödingerova rovnice

V létech 1921-25 se Schrödinger v Curychu zabýval věcmi, které nasál z tradice vídeňské univerzity: statistickou fyzikou, teorií barev, starou kvantovou mechanikou, atomistikou, spektroskopií, teorií specifického tepla. Spektrum jeho zájmů bylo tedy velice široké.

Dostáváme se do doby publikaci Louise de Broglieho. Je všeobecně známo, že v létech 1923 – 1925 se objevily de Broglieovy práce o vlnové mechanice a že tyto práce byly spekulativní, inspirované Hamiltonovou opticko-mechanickou analogií a spíš relativitou než atomovou fyzikou (i když tou ovšem také). Zhruba řečeno, Louis de Broglie postuloval vztah mezi hybnosti a vlnovým vektorem, ale nedovedl najít tvar vlnové funkce ani pravidlo nebo předpis, jak by vlnové funkce měly vznikat. A tady byla šance Schrödingerova, ve které znovu mohl využít tradic vídeňské univerzity (mechanika, problémy vlastních hodnot, statistická fyzika). Je rovněž všeobecně známo, že Schrödinger této šance dokonale využil.

Jak k tomu došlo a které byly Schrödingerovy inspirační zdroje. Zdá se, že byly aspoň dva. Vnější zdroj šel přes P. Debye, jehož upozornil na de Broglieovu disertaci Langevin a jenž navrhl, aby se jí zabývalo kolokvium společné pro curyšskou techniku i univerzitu. Vnitřní inspirační zdroj vycházel ze Schrödingerova zájmu o statistickou fyziku. Einstein ve svém Slánku „Kvantová teorie jednoatomového ideálního plynu“ /12/ používal de Broglieových představ a doporučil je všeobecné pozornosti. To přimělo Schrödingera, aby se de Broglieovými pracemi zabýval. V dopise Einsteinovi Schrödinger konstatuje /13/: „Ostatně celé věc by určitě nevznikla nyní a snad nikdy (alespoň pokud jde o mne), kdyby mě Vaše druhá práce o degenerovaném plynu neupozornila na důležitost de Broglieových myšlenek.“

Tyto a snad i jiné (/3/, str. 258) pohnutky vyvolaly koncem r. 1925 u Schrödingera erupci kreativity a Schrödinger během jediného roku vytvořil dílo, jimi se stal nezapomenutelným. Jádrem je čtyřdílná sekvence „Quantisierung als Eigenwertproblem“ /l4/ a článek „Über das Verhaltnis der Heisenberg-Born-Jordanschen Quantenmechanik zu der meinen“ /15/. Toto dílo je obdivuhodné nejen svou základní myšlenkou, ale i jejími aplikacemi a rozsahem. V těchto článcích je obsažena nejen formulace stacionární i nestacionární Schrödingerovy rovnice, ale aplikace stacionární rovnice na vodíkový atom, na různé typy oscilátorů, rotátorů, teorie stacionárních i nestacionárních poruch, aplikace stacionárních poruch na Starkův jev, teorie disperze, aplikace nestacionárních poruch na buzeni atomů atd.,a to vše s propracovaným matematickým aparátem. Obdivuhodné, fascinující a neuvěřitelné! Během půl roku 170 tiskových stran naprosto originálního textu!

Rozbor těchto prací by trval příliš dlouhou dobu a byl by asi i mimo moje možnosti. Proto mi dovolte, abych jenom uvedl, jak asi Schrödinger dospěl ke své stacionární a nestacionární rovnici. Především chci upozornit na to, že Schrödinger /l4/ studuje Hamiltonovu opticko-mechanickou analogii ve zvláštním q-prostoru, v němž vzdálenost má rozměr součinu délky a odmocniny z hmotnosti. Když si toho čtenář nevšimne, připadá mu většina vztahů druhého sděleni nesprávná už z rozměrových důvodů a ve výsledných rovnicích (rov. (18") druhého sděleni a rov. (4") čtvrtého sděleni) pohřešuje hmotnost m částice. Proto u některých vztahů uvedených v dalším vyznačuji, kterým vztahům odpovídají ve Schrödingerových článcích /14/. (V anglickém výtahu /16/ článků /14/ odvozuje Schrödinger svoji rovnici už v běžném prostoru.) (a) Stacionární rovnici používá Schrödinger již v prvním sdělení k výpočtu vodíkového atomu. Ve druhém sdělení odvozuje její obecný tvar a aplikuje ji na oscilátor a rotátor. Ve třetím sdělení vytváří poruchovou teorii a aplikuje ji na Starkův jev čar Balmerovy série.

Zhruba řečeno, Schrödinger získal stacionární rovnici tak, že nahradil v Helmholtzově (tj. stacionární vlnové) rovnici

platné pro homogenní isotropní prostředí konstantu k² (k = 2 π / λ)  funkcí

kde E je celková a tf potenciální energie. Tak vznikla stacionární Schrödingerova rovnice (rov. (18") druhého sděleni):

Funkci (2) získal Schrödinger právě z Hamiltonovy opticko-mechanické analogie. (Dnes většinou vycházíme z de Broglieova vztahu

, což odpovídá (2).)

Je známo (/17/, /2/ str. 179-180, /3/ str. 257-258), že toto nebyl Schrödingerův první pokus o odvozeni základní rovnice vlnové mechaniky, že napřed vycházel – stejně jako L. de Broglie – z relativistické mechaniky a použil takto získané rovnice k výpočtu pohybu elektronu ve vodíkovém atomu. Protože tehdy se ještě neuvažovalo o spinu, nedostal souhlas s experimentem, zejména v jemné struktuře spektrálních čar (v této souvislosti je zajímavý závěr shrnující anglické verze /16/). Schrödinger se tedy zklamán od těchto problémů na nějaký čas odvrátil a když se k nim po měsících vrátil, odvodil rovnici zhruba tak, jak bylo výše naznačeno.

(b) Nestacionární Schrödingerovu rovnici odvodil Schrödinger na začátku čtvrtého sděleni. Ve vlnové rovnici

nahradil fázovou rychlost u  tzv. normálovou rychlostí ploch konstantní akce

získanou z Hamiltonovy analogie (rov. (6) druhého sdělení). Tím nabyla vlnová rovnice tvaru (rov. (1) čtvrtého sdělení);

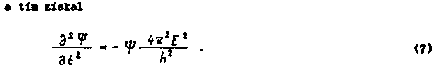
Vyloučením E z rovnic (5) a (7) získal rovnici kmitů membrány (rov. (4) čtvrtého sdělení):

Aby se zbavil derivací čtvrtého řádu, rozložil operátor působící v této rovnici na funkci Ψ(r,t) takto (rov. (4') čtvrtého sdělení):

Tato rovnice je splněna, platí-li jedna z rovnic (rov. (4") čtvrtého sdělení)

což je nestacionární Schrödingerova rovnice.

V závěru čtvrtého sdělení uvažuje Schrödinger o fyzikálním významu vlnové funkce (nazývá ji „Feldskalar“ a │Ψ│² považuje za „jakousi váhovou funkci v konfiguračním prostoru soustavy“). Jeho formulace nelze považovat za náznak statistické kodaňské interpretace, jsou však pozoruhodné: „Vlnově mechanická konfigurace soustavy je superpozici mnoha, přísně vzato všech kinematicky možných bodově mechanických konfiguraci. Přitom každá bodově mechanická konfigurace přispívá ke skutečné vlnově-mechanické konfiguraci určitou vahou, jež je dána právě výrazem │Ψ│2. Má-li někdo rád paradoxy, může říci, že se soustava nachází jakoby ve všech kinematicky myslitelných polohách současně, ale ne ve všech ve stejné míře. Při makroskopickém pohybu se váhová funkce prakticky stáhne na malý obor prakticky nerozlišitelných poloh, jehož těžiště urazí v konfiguračním prostoru pozorovatelnou vzdálenost. Při mikroskopických pohybových problémech se zajímáme v každém případě také, a v jistých otázkách dokonce v prvé řadě, o měnící se rozložení v tom oboru.“

V té době – začátkem a v prvé polovině r. 1926 – však již existovaly nejen stará kvantová mechanika a de Broglieovy práce, ale také nová kvantová (maticová) mechanika, zejména proslulá „Dreimanner Arbeit“ autorů Borna, Heisenberga a Jordana /18/, která popisovala atomové jevy neméně dobře jako Schrödingerova vlnová mechanika. Byla to dosti kuriózní situace: existovaly dvě fyzikálně ekvivalentní, avšak matematicky zdánlivě nesouvisející teorie. Je ovšem všeobecně známo, že sám Schrödinger /15/ a vzápětí Carl Eckart /19/ velmi brzy objasnili vztah („formální matematickou totožnost“ /15/) obou teorií, Schrödinger dokonce hned po druhé části své čtyřdílné sekvence /14/. Časové schéma těchto prací ukazuje obrázek.

Schrödingerovy práce byly ihned nadšeně přijímány, neboť dávaly naději, že dovolí odstranit z fyziky kvantové skoky. Byly založeny na matematické analýze a diskrétní vlastní hodnoty parciálních rovnic (o něž tehdy především šlo) byly přijatelným produktem spojitých vlnových funkci. Příbuznost s problémy teorie vlnění také způsobovala, že Schrödingerovy práce byly mnohem přijatelnější než abstraktní a tehdy nezvyklý maticový přístup Heisenbergův, Bornův a Jordanův. Kromě toho Schrödingerovy práce nabízely nadějné a krásné završení staleté opticko-mechanické analogie. Byly tedy vítány Einsteinem, Planckem, Sommerfeldem, W. Wienem a vůbec většinou fyziků. Pouze Bohr, göttingenští a několik málo jiných fyziků je přijímalo zdrženlivě.

Koncem jara 1926 pozval Sommerfeld Schrödingera do Mnichova, aby uspořádal seminář. Tam došlo k diskusi mezi Schrödingerem a Heisenbergem, ve které zůstal Heisenberg osamocen /20/. Jeho hlavní námitkou bylo, že Schrödingerova teorie je nekonzistentní, neboť už pojem potenciální energie, potřebný pro vyjádření rychlosti vlnění, je vzat z korpuskulární teorie, a že Schrödingerova teorie nedokáže vysvětlit Planckův vyzařovací zákon. W. Wien ho vSak odbyl názorem, že to je otázkou blízké budoucnosti. Heisenberg o tom okamžitě napsal Bohrovi a ten pozval Schrödingera na září do Kodaně. Diskuse s Bohrem začala hned na nádraží. Schrödinger ovšem bydlel v Bohrově domě, takže nebylo důvodu diskusi přerušovat. Bohr, vždy jemný a přátelský, se změnil v bezcitného a neústupného fanatika /20/ a Schrödinger s tomu odpovídající rozhodností hájil svá stanoviska. Zdá se, že jistého vrcholu dostoupila diskuse při Schrödingerově zvolání: „Mají-li tu ty prokleté kvantové skoky opravdu zůstat, pak mne mrzí, že jsem se vůbec kvantovou teorií zabýval“. Zdvořilá Bohrova odpověď („Ale my ostatní jsme vám nesmírně vděčni, že jste tak učinil. Vaše vlnová mechanika přispěla natolik k matematické jasnosti a jednoduchosti, že představuje obrovský pokrok ve srovnání se všemi předešlými formami kvantové mechaniky.“) nezabránila, aby Schrödinger z únavy a rozrušení neonemocněl. To však zase nezabránilo Bohrovi pokračovat v diskusi ... /20/.

Nakonec to Schrödinger přece jen přežil. V zimě r. 1926/27 absolvoval ještě dvouměsíční přednáškové turné po Severní Americe, a tím končí Schrödingerovo curyšské období.

Zbývá ještě upozornit na jednu drobnost, která je však důležitá z hlediska popularizace těchto věcí u nás. Kapicovou zásluhou – nebo spíš vinou – se totiž u nás rozšířil názor, jako by Schrödingerova rovnice vznikla v učebním procesu, ve kterém Debye Schrödingera vedl. Poslechněme si nejdříve, co o tom říká Debye v jednom pozdějším interview /21/: „... Pak de Broglie publikoval svůj článek. V té době byl Schrödinger mým nástupcem na univerzitě v Curychu a já jsem byl na technice, což je federální instituce, a měli jsme společné kolokvium. Mluvili jsme o de Broglieově teorii a shodli jsme se, že jí nerozumíme a že bychom se měli zamyslet nad jeho formulacemi a jejich významem. Tak jsem požádal Schrödingera, aby pro nás udělal kolokvium. A jeho příprava ho skutečně přiměla začít.“

Kapica v přednášce „Profesor a student“ na jednom večírku převyprávěl celý příběh takto /22/: ""Mohu uvést ještě jeden příklad. Vyprávěl mi ho známý fyzik Debye. Tehdy byl profesorem v Curychu a s ním tam přednášel i jeho žák Schrödinger, tehdy zcela neznámý mladý fyzik.

V tu dobu se objevila de Broglieho hypotéza vlnové struktury elektronu. De Broglie dokázal, že při určitých podmínkách interference lze pohyb elektronu vyjádřit pohybem vlny. K návrhu ekvivalence vlnových a kvantových procesů, vlnového pohybu a pohybu korpuskulárního se celá řada fyziků stavěla odmítavě. Nepřijal jej ani Schrödinger. Když ho Debye požádal, aby o de Broglieho práci udělal pro studenty přednášku, odmítl. Ovšem později, když Debye uplatnil svou profesorskou autoritu a požádal ho ještě jednou, Schrödinger se podrobil a začal přemýšlet, jak de Broglieho ideje formulovat v co nejúspornější a nejpřesnější matematické formě. A když o nich potom přednášel, formuloval je matematicky tak, jak to považoval za nejlepší. Tehdy mu Debye řekl: „Poslyšte, vždyt vy jste našel novou rovnici, fundamentální rovnici moderní fyziky.“

Výsledkem pedagogické činnosti bylo tedy nalezení vlnové rovnice, základní rovnice moderní fyziky.""

To ovšem není pravda v mnoha ohledech. Schrödinger už nebyl právě mladý, bylo mu 38 let, nebyl neznámý, byl znám mnoha pracemi, také pracemi o teorii barev, v nichž používal neeuklidovských prostorů k popisu barev, a především nebyl Debyeův žák, ale kolega, všeho všudy o tři roky mladší, a už vůbec to nebyla povaha, na niž by bylo vhodné uplatňovat profesorskou autoritu.

Tak se to tedy vypráví na Rusi. Ohlas písní ruských u nás zní takto /23/: ""Ačkoliv Debye svým vlastním vědeckým dílem podstatně nepřispěl k rozvoji kvantové mechaniky, měl o ni nemenší zásluhu v roli učitele. Líčí to P. L. Kapica podle vyprávění P. Debye. Za působení v Zurichu uložil Debye mladému asistentovi Schrödingerovi, aby nastudoval de Broglieho hypotézu o vlnovém charakteru elektronu a připravil o tom přednášku pro studenty. Schrödinger se prý k tomuto úkolu zpočátku stavěl odmítavě, pak ale přednášku připravil. Debye ji komentoval slovy: „Poslyšte, vy jste našel novou rovnici, fundamentální rovnici moderní fyziky.“ ""

To je příklad poněkud uvolněné popularizace. Ale to se stává, proto by se přednášky neměly zaznamenávat.

Berlínské období 1927 – 1933

V roce 1927 bylo Schrödingerovi nabídnuto, aby se stal členem Pruské akademie věd a profesorem teoretické fyziky na berlínské univerzitě, tedy nástupcem Maxe Plancka, jenž se blížil své sedmdesátce. tj. věku, kdy tehdy němečtí univerzitní profesoři odcházeli do důchodu. Schrödinger jistou dobu váhal, neboť se mu v Curychu líbilo a Curych si ho snažil udržet tím, že mu nabídl dvojitou profesuru, na technice i univerzitě. Pozvání do Berlína se však nedalo odolat, neboť Berlín byl tehdy skutečným středem fyzikálního světa. Byl sídlem mnoha vědeckých institucí, městem se slavnou univerzitou i technikou, a především místem, kde působili Einstein, Planck, Laue, G. Hertz, P. Pringsheim, Ladenberg, Hahn, Meitnerová, Nernst a mnoho dalších, tehdy mladých fyziků (Gabor, Neumann, Wigner, Szilard, F. London atd.). Zdá se, že Planckovo vyjádření, že by ho těšilo, kdyby našel ve Schrödingerovi svého nástupce, nakonec rozhodlo.

Berlínské období označuje Schrödinger za „dobu učení a učení se“ /5/. Navázal mnoho známostí, navštěvoval – jako většina jeho slavných kolegů – proslulý Laueův středeční seminář a přednášel na univerzitě. O jeho přednáškách se před nedávném objevilo svědectví prof. N. Kurtiho /24/ na semináři o vzdělávání mezi válkami: Navštěvoval v r. 1928 v Berlíně přednášky Schrödingera, Plancka, Pringsheima, Ladenberga, Simona a von Laueho – „Schrödinger 's being the most brilliant“. že Schrödinger uměl znamenitě přednášet, jsem již řekl, ale že jeho přednášky vynikaly i v této „konkurenci“, je jistě pozoruhodné.

Útěky před nacismem

Čas běžel, přišel 30. leden 1933 a Hindenburg jmenoval Hitlera říšským kancléřem. Tehdy se fyzici, jako všichni, rozdělili do tři skupin ve smyslu výroku sv. Augustina (dopis 95): „Je také velmi nebezpečné, říkáme-li co si myslíme, velmi bolestné, neříkáme-li to, a velmi zhoubné, říkáme-li opak.“ Schrödinger – aspoň co se týká veřejných projevů – volil cestu bolestnou a byl shledán spravedlivým. Jeden autor /25/ sice uvádí, že se Schrödinger snažil zabránit akci SA v židovském ghetu a že nebyl ubit jen proto, že byl poznán. Je to však údaj ojedinělý, který je ovšem těžko vyvracet. Schrödinger se o tom, pokud vím, nikde nezmiňuje. Také se mi nezdá, že by oddíl SA v akci poznal Schrödingera.

V soukromí a odborných kruzích Schrödinger své odmítavé stanovisko k nacismu vyjadřoval. V té době byl v Berlíně na návštěvě pozoruhodný člověk, který se jmenoval F. A. Lindemann (v encyklopediích ho však pod tímto jménem nehledejte, ale pod jménem Cherwell, l^st Viscount and Baron of Oxford). Narodil se (1886) v Baden-Badenu, studoval na univerzitách v Německu a Francii a už za 1. světové války byl ředitelem fyzikální laboratoře R. A. F. Od roku 1919 byl profesorem experimentální fyziky v Oxfordu a ředitelem Clarendon Laboratory, kterou povznesl z běžné laboratoře k světové proslulosti. Znalci života sira Winstona vědí, že poté, co Německo vypovědělo válku Polsku, byl Churchill povolán znovu do britské vlády ve funkci prvního lorda Admirality. Ministerský předseda Chamberlain mu však nedával dost informací, a tak si Churchill zřídil vlastní zpravodajskou službu, v jejímž čele stál profesor Lindemann. Rázem se Churchill stal nejlépe informovaným ministrem ve vládě /26/. Za 2. světové války byl Lindemann Churchillovým poradcem pro organizaci techniky a vědy a po válce poradcem vlády pro atomové otázky. Zemřel v r. 1957 v Oxfordu.

Nuže, tento Lindemann byl v r. 1933 v Berlíně jistě také proto, aby zprostředkoval propuštěným fyzikům židovského původu zaměstnání v Británii. V soukromém rozhovoru s ním Schrödinger naznačil, že by přijal místo v Anglii.

Prázdniny r. 1933 trávil Schrödinger v italském Jižním Tyrolsku spolu s Bornem a Weylem. Odtud poslal do Berlína demisi, „na kterou dlouho neodpovídali, pak ji zapřeli, nakonec ji nepřijali, protože mezitím obdržel Nobelovu cenu za fyziku“ /5/. Z Jižních Tyrol odejel Schrödinger do Oxfordu, kde se Lindemann postaral o jeho přijetí do Magdalen College jako fellow placený Imperial Chemical Industries a bez povinnosti přednášet.

V r. 1936 mu byla nabídnuta profesura jednak v Edinburghu, jednak ve štýrském Hradci. Schrödinger se rozhodl pro Štýrský Hradec. Toto rozhodnutí se nám může jevit nepochopitelné – odchod z jedné z nejslavnějších anglických univerzit na provinční univerzitu ve žhavém středoevropském prostoru. Schrödinger sám to později označil za „bezpříkladnou hloupost“ /5/, jeho manželka za naprosté politické ignorantství, ale někteří jeho životopisci /2/ to považují za rozhodnutí ovlivněné steskem po domově. Kromě toho lze u Schrödingera vycítit i jakousi nesourodost s britským prostředím. Schrödinger asi také viděl ve Štýrském Hradci místo proslavené Boltzmannovými objevy. Schrödinger ovšem nikde nic podobného nenaznačuje. Vidím v tom opět projev jeho autostylizace. Těžko uvěřit, že by člověk, jenž má za přítele Lindemanna, mohl mít nedostatek základních informací pro svá rozhodnutí.

Nicméně Schrödinger byl od r. 1936 ve Štýrském Hradci. V březnu 1938 Německo zabralo Rakousko a Schrödinger se octl opět v „Říši“ a hlavně pod nacistickou vládou. Schrödinger neměl sice potíže rasové povahy, ale jeho odchod z Berlína byl považován za akt nepřátelský Říši. A nyní nastává doba jistého Schrödingerova ponížení. Našel jsem v Nature /27/ v rubrice News and Views tuto noticku: ""Od nedávného začlenění Rakouska do Německa je k dispozici málo přesných informací o výsledku a změně místa některých význačných mužů vědy. Na dotaz jsme byli informováni, že Prof. E. Schrödinger bude i nadále vedoucím katedry teoretické fyziky na univerzitě ve Štýrském Hradci. Hradecký Tagespost ze 30. března zveřejňuje dopis Prof. Schrödingera Senátu univerzity, ve kterém vysvětluje, že až dosud nebyl aktivní v nacionálně socialistickém hnutí, ale že je rád, že je nyní do něho začleněn. Poslední odstavec jeho dopisu zní takto: „Příznivci, kteří přeceňují můj význam, považují za správné, aby kajícná zpověď, kterou jsem u nich vykonal, byla zveřejněna. Také já patřím k těm, kteří se chápou podané ruky míru, neboť, poněvadž jsem seděl u svého psacího stolu, neodhadl jsem správně až do posledka skutečnou vůli a věrný osud své země. Dělám tuto zpověď ochotně a radostně. Věřím, že mluvím ze srdcí mnohých, a doufám, že, když tak činím, sloužím tím své zemi.“ ""

Naštěstí Schrödinger vykonal „kajícnou zpověď“ na nepravém místě a nebyla mu mnoho platná. K 1. září 1938 byl Schrödinger propuštěn. Schrödinger zajel do Vídně a zachovala se tato zpráva o rozhovoru mezi ním a chápajícím ministerským radou /2/: „No, jistě si najdete pěkné místo v průmyslu.“ Schrödinger: „Pro teoretického fyzika to není úplně snadné ... Budu asi muset opět odejít do ciziny.“ Ministerský rada pak upozornil na nebezpečí, o kterém Schrödinger asi neuvažoval: „Ano, máte vůbec ještě své pasy?“ Výjezdní doložky tehdy v Německu nebyly, a tak byli Schrödingerovi do tří dnů pryč. Odjeli do Říma, sice „se zpátečními jízdenkami, ale bez vůle k návratu“ /2/, s deseti markami.

V Římě Schrödingera finančně podpořila papežská akademie, jejímž byl Schrödinger členem. Irské vyslanectví v Římě mu pomohlo s vízovými problémy. Proč irské vyslanectví?

Zde se nám při líčení Schrödingerova života objevuje další postava, jejíž životní osudy by poskytly materiál pro mnoho románů: Eamon de Valera, nejvýznamnější irský politik našeho století. Narodil se v New Yorku. Jeho otec byl americký Španěl a matka Irka. Vystudoval v Irsku a působil určitou dobu jako učitel matematiky. Především to však byl bojovník za svobodu Irska. Vidíte z průsvitky, že v r. 1916 byl odsouzen k smrti, bylo to pro účast v Casementově povstání (šlo také o to, aby irští vojáci nebojovali v 1. světové válce za britské zájmy). Jeho poprava však byla odročena (na rozdíl od Casementovy), protože si Británie nechtěla pohněvat Spojené Státy, a po válce byl de Valera amnestován. Když bylo v r. 1921 zřízeno dominium Svobodný stát irský, bojoval de Valera dále za naprostou nezávislost. Dosáhl jí až v r. 1937, kdy byla vyhlášena nezávislá a neutrální Irská republika v rámci britského Společenství národů, z něhož se oddělila v r. 1949. De Valera byl dlouholetým ministerským předsedou a presidentem Irské republiky.

V druhé polovině třicátých let už byl de Valera ministerským předsedou a zamýšlel založit Dublin Institute for Advanced Studies po způsobu princetonského ústavu. Bylo mu sympatické, že Schrödinger svým dílem oživil a oslavil mechaniku slavného irského učence Hamiltona, a proto s ním už za jeho pobytu ve štýrském Hradci jednal o spolupráci.

V době Schrödingerova pobytu v Římě úřadoval ministerský předseda Irska E. de Valera v Ženevě jako president Společnosti národů. Není tedy divu, že irské vyslanectví v Římě zajistilo Schrödingerovi víza téměř do všech evropských států. Přesto byli Schrödingerovi na italsko-švýcarských hranicích zdrženi. Našlo však o službu celníků fašistické Itálie nacistickému Německu, ale o mnohem prostší záležitost. Italští celníci podezřívali Schrödingera, že je mezinárodním velkopašerákem, protože cestoval s vízy do téměř všech evropských států, avšak bez peněz. Poměry se mění; dnes by si mysleli, že jde o prominentního vědeckého pracovníka cestujícího na reciprocitu. Zdržení bylo ostatně krátké, a tak se Schrödingerovi dostali do švýcarská.

Bylo to období „Mnichovské dohody“ (což je oficiální označeni pro mnichovskou zradu) a de Valera cítil akutní nebezpečí války. Proto se Schrödinger zdržel v Ženevě jen 3 dny a odjel přes Curych do Oxfordu. Dublinský ústav nebyl ještě založen, a tak po dvou měsících v Oxfordu působil Schrödinger od prosince 1938 do záři 1939 jako hostující profesor na univerzitě v Gentu v Belgii. Schrödingerovi měli německé pasy, a tak byli po vypuknuti války považováni za „nepřátelské cizince“. S pomoci de Valery a Lindemanna vsak mohli odcestovat přes Anglii do Irska.

Profesorem v Dublinu (1939 – 1956)

Sedmnáctiletý pobyt v Dublinu označuje Schrödinger za „velice, velice krásnou dobu“ /5/, str. 38. V r. 1940 byl zřízen Dublin Institute for Advanced Studies, jenž měl tehdy jen dvě odděleni: Odděleni keltské jazykovědy a odděleni teoretické fyziky. Schrödinger pracoval v mnoha oborech: matematice, statistické fyzice, kvantové mechanice, relativitě, unitární teorii poli, kosmologii, filosofii. Napsal v této době 65 publikaci, tj. téměř polovinu vdech svých odborných publikaci, mezi nimi i slavnou populární knihu What is life?/28/ a učebnici Statistical thermodynamics /29/. Schrödinger pořádal letní školy, jichž se zúčastňoval také Dirac, Born a ministerský předseda de Valera. U Schrödingera také pobývali stipendisté z celého světa na dlouhodobých stážích. Z Československa to byl prof. M. Brdička v roce 1948/49.

Dublinské období se Schrödingerovi líbilo do té míry, že nelitoval toho, že šel do Štýrského Hradce a nepřijal místo v Edinburghu, neboť odtud by nemohl do Dublinu přejit: „Dublin byl pro mne stokrát výhodnější, protože v Edinburghu bych musel těžce pracovat a během celé války bych byl enemy-alien.“ (/5/, str. 37) ""... nikde jinde bychom neprožili strašlivou nacistickou válku tak bez žalu, že je to až zahanbující. Nelze domyslit, kdybych místo toho měl sedmnáct let ve Štýrském Hradci „mlátit prázdnou slámu“, ba i bez nacistů a bez války. Často jsme si potichu říkali: „Děkujeme našemu Vůdci.“ "" (/5/, str. 38)

Po válce zval rakouský president K. Renner Schrödingera zpět do vlasti, ale de Valera ho od návratu odradil vzhledem k „nevyjasněné situaci ve střední Evropě“. Schrödingerovi „bylo ještě deset let v Dublinu (1946 – 1956) velmi užitečných, zčásti pro větší počet útlých knížeček v angličtině vydaných v Cambridge University Press, zčásti kvůli práci na ,nesymetrické‘ zobecněné teorii gravitace, která asi zklame; last but not least, kvůli velmi úspěšnému odstranění šedého zákalu na obou očích ...“ /5/, str. 39.

Profesorem ve Vídni (1956 –1961)

Jakmile se stalo Rakousko neutrálním státem, vrátil se Schrödinger do Vídně. Vídeňská univerzita pro něho zřídila zvláštní profesuru, kterou prodlužovala i po Schrödingerově sedmdesátce. Schrödinger byl zahrnován různými poctami, cenami etc, jimiž mu jeho tehdejší i dřívější spoluobčané a instituce vyjadřovali úctu.

Bohužel, zdraví už mu nesloužilo. V r. 1957 překonal nebezpečné onemocnění, a plné zdraví už se nevrátilo. Zemřel 4. ledna 1961. Je pochován v malé tyrolské vesničce Alpbachu, která je dnes známá schůzkami Evropského fóra. Jeho hrob prý není nijak nápadný a nese nápis: R. I. P. Erwin Schrödinger 12. VIII. 1887 – 4. I. 1961.

Závěrem

Schrödinger se stal nezapomenutelným svou rovnicí. Zdá se však, že pro něho samého byla důležitější jeho přírodní filosofie než sama fyzika, resp. že fyzika byla jen pokračováním jeho filosofie. Je to neuvěřitelné u člověka, jenž tak rozhodným způsobem ovlivnil vývoj fyziky. Odpovídá tomu někdy i styl jeho vědeckých článků. Nevěnuje mnoho pozornosti vymezení nebo definici pojmů, jichž používá, ale předpokládá – jak to řekl o Platónově vyjadřování – , že používáním pojmy samy vyjeví svůj význam. (Tím se velmi liší např. od stylu fyzikálních děl Machových.) Jeho filosofické názory jsou asi tradiční,;věnoval se hodně řecké filosofii, přijímal Spinozu, Schopenhauera a Macha. Filosofické ohledy byly asi také hlavní příčinou, proč odmítal kodaňskou interpretaci kvantové mechaniky. Jeho dominantní zájem o filosofii je patrný i z jeho vlastního životopisu /5/» v němž se podivuhodně málo zmiňuje o svých hlavních fyzikálních výsledcích.

Schrödingerovy populární knížečky jsou mistrovská díla poučné pro kultivovaného laika i specfialistu. fiíkává se o nich, že jsou i stylisticky dokonalá. To se mi však nezdá. Připadá mi někdy, že jsou psaná směsicí až slangu a literární řeči. (Potvrdili mi to i lidé, jimž je angličtina nebo němčina mateřským jazykem.) V každém případě však stojí za námahu se jimi prokousat. Platí to i o nejznámější z nich, „What is life?“, i když ji Elsasser /1/ poněkud kritizuje.

Jistou pozornost v těchto spisech věnuje Schrödinger vztahu vědy a náboženství. Otěchto věcech se však těžko s určitostí mluví. Schrödinger rozhodně nebyl materialistickým myslitelem. Elsasser /l/ naopak zdůrazňuje jeho katolické zázemí. Ale to se mi také nezdá, neboť se o některých věcech vyjadřuje příliš zlehčeně, a to i ke konci svého života. Byl svým náboženským cítěním asi blízký Einsteinovi, jenž věřil v boha Spinozova, tedy ne v osobního Boha, který s láskou shlíží k lidem, ale v boha, který se nezajímá o dobro a zlo, které lidé konají. Schrödingerův zájem o biologii možná také způsobil, že mu byla blízká Schweitzerova nauka úcty k životu /30/. Schrödinger v těchto oblastech celý život hledal. Kupodivu, zdá se mi, jako by křesťanství míjel – na rozdíl např. od Maxwella, Plancka nebo Laueho – , a podobně jako Mach se obracel k orientálním náboženstvím. Věděl, co přináší člověku víra v osobního Boha, ale cestu k němu asi nenašel. Zlehčené formulace, o nichž jsem se zmínil, se ovšem netýkají otázek víry, ale nejčastěji výuky a katechetů. Zazlíval jim dogmatický přístup k výuce, který vylučuje nepohodlné otázky a vytváří tabu. To Schrödinger a zřejmě traumatizovalo a na několika místech se o tom zmiňuje (viz např. /5/, str. 13, 26, 27). Zdá se mi, že i toto je vhodné uvést, neboť to ukazuje, jak zformalizovaná výuka dovede člověku ublížit v jeho celoživotní potřebě.

Zdůraznil jsem na začátku, že Schrödinger byl vzdělancem s velice širokými kulturními zájmy. Otec v něm inspiroval zájem o výtvarné umění a biologii. V umění však byla asi vlastní Schrodingerovou oblastí poezie. Překládal i psal původní poezii a vydal sbírku básní. Mají dokonalou formu a připomínají někdy Rilkeho. Schrödingerovo kulturní zázemí mu také asi umožnilo, aby jeho kreativita neklesala s rostoucím věkem i věhlasem.

Vážené kolegyně a kolegové, Schrödingerova rovnice je v našem povědomí termínem, v němž Schrödingerovo jméno specifikuje rovnici. – Jsem proto rád, že jsem zde mohl připomenout i Schrödingerovy osudy.

Děkuji Vám za pozornost.

Poděkování

Paní Z. Kučerové děkuji za diskuse nad Schrödingerovými díly a za některé překlady a paní V. Kolaříkové za vyhotovení strojopisu. Kolegovi M. Černohorskému a kolegyni M. Fojtíkové vděčím za připomínky k textu.

Literatura

Seznam odborných publikaci E. Schrödingera je uveden např. v knihách /2/ a /4/.

1. Elsasser W. M.: Memoirs of a Physicist in the Atomic Age. Science History Publications, New York 1978, Adam Hilger Limited, Bristol 1978, 130-140.

2. Hermann A.: Erwin Schrödinger – Eine Biographie. Ve sborníku Erwin Schrödinger: Die Wellenmechanik. Ernst Battenberg Verlag, Stuttgart 1973, 173-192.

3. Jammer M.: The Conceptual Development of Quantum Mechanice. McGraw Hill, Inc. New York 1966, 255-280.

4. Polak L. S.: Erwin Schrödinger i vozniknovenie kvantovoj mechaniki. Ve sborníku Erwin Schrödinger. Izbrannye trudy po kvantovoj mechanike, ed. L. S. Polak. Izdatelstvo Nauka, Moskva 1976, 347-392.

5. Schrödinger E.: Mein Leben. Meine Weltansicht. Nakladatele a místo vydáni neznám, 1985.(Poškozený antikvariátní výtisk.)

6. Erwin Schrödinger. Ve sborníku Les Prix Nobel en 1933. Stockholm 1935, 86-88. Viz též /4/, 343-346.

7. Blackmore J. T.: Ernst Mach. His life, work and influence. University of California Press, Berkeley, Los Angeles, London 1972.

8. Brdička M.: Deset let od úmrtí prof. dr. Erwina Schrödingera. Čs. čas. fys. A 21 (1971), 456-458.

9. Schrödinger A.: Erwin Schrödinger, 1887 – 1961. V knize Schrödinger E.: Was ist ein Naturgesetz? 2. unveranderte Auflage, R. Oldenbourg, Munchen 1967, 144-146.

10. Herneck F.: Průkopnici atomového věku. Orbis, Praha 1974, 75, 126-127, 211.

11. Laue M. v.: My Development as a Physicist. Ve sborníku Fifty, Years of X-ray Diffraction, P. Ewald, ed. N.- V. A. Oosthoek s Uitgeversmaatschappij, Utrecht 1962, 278-307, zejména 8. 297.

12. Einstein A.: Quantentheorie des einatomigen idealen Gases. Zweite Abhandlung. Sitzungsber. preuss. Akad. Wiss., Phys.-math. Kl., 1925, 3-14.

13. Schrödinger E.: Briefe zur Wellenmechanik. Schrödinger - Planck, Einstein, Lorentz, ed. K. Przibram. Springer Verlag, Wien 1963, 24.

14. Schrödinger E.: Quantisierung als Eigenwertproblem. Annalen der Physik (4) 79 (1926), 361-376; 489-527; 80 (1926), 437-490; 81 (1926), 109-139.

15. Schrödinger E.: Über das Verhältnis der Heisenberg-Born-Jordanschen Quantenmechanik zu der meinen. Annalen der Physik (4) 79 (1926), 734-756.

16. Schrödinger E.: An undulatory theory of mechanics of atoms and molecules. Phys. Rev. 28 (1926), 1049-1079.

17. Dirac P. A. M.: Professor Erwin Schrödinger - Obituary. Nature 189 (1961), 355-356.

18. Born M., Heisenberg W., Jordan P.: Zuř Quantenmechanik II. Zeitschrift fur Physik J5_ (1926), 557-615.

19. Eckart C: Operator calculus and the solution of the equations of quantum dynamics. Phys. Rev. 28 (1926), 711-726.

20. Heisenberg W.: Physics and beyond. Harper & Row, Publishers, New York 1971, 70-81.

21. Peter J. W. Debye: An Interview. Science 145 (1964), 554-559.

22. Kapica P. L.: Experiment, teorie, praxe. Mladá fronta, Praha 1982, 250.

23. Čs. čas. fyz. A 34 (1984), 616-618.

24. Education between the wars. European Journal of Physics 7 (1986), 148-150.

25. Cropper W. H.: The Quantum Physicists. Oxford University Press, New York, London, Toronto 1970, 100.

26. Matějka J.: život sira Winstona, třetí sešit. Horizont, Praha 1970, 34.

27. Nature No 3577, May 21, 1938, 929.

28. Schrödinger E.: What is life? Cambridge University Press, Cambridge 1944.

29. Schrödinger E.: Statisical Thermodynamics. Cambridge University Press, Cambridge 1946.

30. Schweitzer A.: Nauka úcty k životu. Lyra Pragensis Praha 1974.

„

JEŠTĚ O ČASE

Jan Novotný

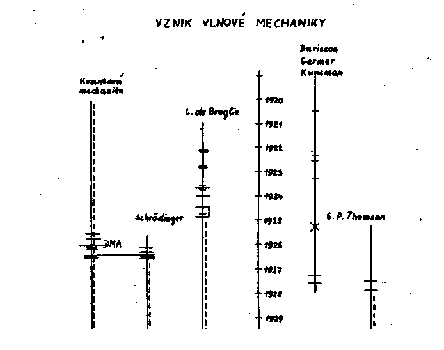
Katedra teoretické fyziky a astrofyziky PřP UJEP 611 37 Brno, Kotlářská 2

Tento doplněk k mému příspěvku v Dialozích 1 (D1/31-38) je pokusem více vyhovět záměru organizátorů „zabývat se tím, jak by ve fyzikálním vzdělávání na různých úrovních měly být budovány, resp. zaváděny vybrané pojmy“ /1/. Zároveň zahrnuje některé náměty, které přinesla diskuse v pracovní skupině A3.

Jak jsem se snažil ukázat, čas vystupuje v lidské zkušenosti i ve vědách zejména v těchto podobách:

(1) Doba trvání objektu mezi dvěma událostmi – vlastní čas.

(2) Datum umožňující – spolu s prostorovými souřadnicemi – identifikaci události – čtvrtá souřadnice.

(3) Ukazatel směru vývoje od minulosti k budoucnosti – šipka času.

(4) Hranice mezi tím, co se již stalo, a co se teprve stane, realizace událostí – přítomnost.

Aspekty (1) a (2) byly již fyzikou velmi hluboce pochopeny a popsány. Toto poznání, obsažené zejména v díle I. Newtona a A. Einsteina, lze považovat za pevný základ, který asi ani dalším vývojem fyziky nebude podstatně změněn, i když může být ze strany kvantové fyziky a kosmologie podložen hlouběji /2/. Proto je předmětem výuky na řadě úrovní. V našem náčrtu, jak by mohly být představy o čase zaváděny, se soustředíme hlavně na tento pevný základ (aspekty 1 a 2).

1. Vlastní čas

Doba trvání může být měřena hodinami. což je v nejobecnějším smyslu dostatečně hustá řada rozlišitelných událostí spojených s daným objektem. V souladu s naším spojitým vnímáním času a možností zjemňovat časovou stupnici vkládáním dalších událostí považujeme údaj hodin za reálné číslo. Zkušenost ukazuje, že hodiny založené na periodických procesech různého druhu mají – alespoň přibližně – tyto vlastnosti:

(a) Poměry časových intervalů měřených různými hodinami zůstávají během jejich společného pohybu konstantní.

(b) Tvrzení (a) platí i v případě, že v mezidobích se hodiny pohybovaly různě.

První skutečnost je projevem nezávislosti fyzikálních zákonů na čase – homogenity času – , druhá vyjadřuje jeho integrabilitu – možnost jednoznačného přenosu zvolené časové jednotky.

Poznamenejme, že požadavky (a), (b) nejsou apriorní nutností. V historii fyziky sehrály roli i teorie s neintegrabilním časem /3/ či s rozdílnými mírami času /4/. Současná fyzika však ukazuje (např. /5, 6/), že jejich platnost je nejen s vysokou přesností zaručena u hodin atomových, ale potvrzuje se i teoreticky tím, že případná odchylky lze vysvětlit jako projev vnějších vlivů a mohou být korigovány. Tak dospíváme k pojmu ideálních hodin, které měří vlastní čas. Vlastní čas  τ je (při zvolené časové jednotce) délkou světočáry. která již nemusí odpovídat reálnému pohybu hodin – je to doba trvání, kterou by změřily ideální hodiny, pokud by se daným způsobem pohybovaly. Znalost fyzikálních zákonů umožňuje extrapolovat pojem délky světočáry i do oblastí, v nichž ani atomové hodiny nemohou fungovat, jako je tomu v raných fázích kosmologického vývoje.

2. Čtvrtá souřadnice

Hodiny, které vyplňují dostatečně hustě jistou prostorovou oblast, definují v ní vztažný systém. (Předpokládáme, že jsou prakticky bodové a vzájemně se nesrážejí – může přitom jít o hodiny pouze myšlené, tj. o soubor parametrizovaných světočar.) Jednotlivé hodiny jsou rozlišeny trojicí prostorových souřadníc x^α (α = 1, 2, 3), které mohou být křivočaré. Pro rozlišení událostí je třeba zadat ještě čtvrtou souřadnici, kterou je údaj na hodinách t = x⁴ , tedy souřadnicový čas. Tak dospíváme k pojmu čtyřrozměrného prostoročasového kontinua.

Čas t nemusí být vlastním časem. Po hodinách, které jej určují, požadujeme pouze, aby se nezastavovaly. Časová data na různých světočárách je však vhodné vázat podmínkou, která je dosti přísná. Existuje-li jistá mezní rychlost šíření signálů c (podle teorie relativity rychlost světla), nemělo by být možné spojit události o stejném t signálem o rychlosti v ≤ c . Jinými slovy události o stejném t nemohou být příčinně spojeny (problémy ohledně existence tachyonů a jejich vztahu k příčinnosti zde necháváme stranou). Soubor hodinek účastníků našeho semináře tuto podmínku určitě nesplňoval. Zvolíme-li pevně t na Zemi, pak interval, v jehož rámci může být voleno t na Měsíci, je asi 3 s. Pomalost našich relativních pohybů ve srovnání s rychlostí světla způsobuje, že vzdálenost k Měsíci se nám jeví „velká“ ve srovnání se sekundou. Proto v běžném životě i v předrelativistické fyzice je považována mezní rychlost za nekonečnou, což má za následek jednoznačné stanovení okamžiku t = konst na všech hodinách, a tedy zavedení absolutní současnosti newtonovské fyziky.

Avšak i mimo newtonovskou fyziku by mohlo být výhodné podrobit časovou souřadnici podmínkám

(i) čas t je identický s vlastním časem τ (se společnou jednotkou na všech hodinách) a

(ii) současnost t = konat je volena tak, aby odpovídala synchronizaci hodin pomocí výměny signálů o mezní rychlosti.

Vztažný systém s touto volbou časové souřadnice se nazývá systémem synchronním. V předrelativistické fyzice s jednoznačně určenou současností byla synchronizace ideálních hodin nezávislá na jejich pohybu. Proto jsou běžné představy a čase spjaty s jednoznačnou synchronizací hodin a překonání těchto představ v díle klasiků teorie relativity znamenalo překročení obtížné psychologické bariéry /7/. I podle obecné teorie relativity je možno synchronní systémy vždy najít, jsou však realizovány pomocí volně padajících hodin. Např. pro popis gravitačního pole Země je synchronní systém zpravidla méně výhodný než statický systém, v němž synchronizaci uskutečnit nelze.

V prostoročase bez gravitačního pole, jímž se zabývá speciální teorie relativity, existují synchronní systémy, v nichž se vzdálenost hodin s časem nemění a prostorová geometrie je eukleidovská. Těchto inerciálních systémů se pak většinou užívá. Také ve Friedmannových kosmologických modelech je výhodné užívat synchronního systému, vzhledem k němuž je izotropní reliktní záření. Synchronní systémy nám proto postačí pro výuku velké části fyziky, je však užitečné si uvědomit, že jejich existence není samozřejmá.

Naznačme ještě, jak lze uvedená fakta formulovat matematicky. (Podrobnější poučení najde čtenář např. v /8/ nebo /9/; v obou knihách je spojeno i s hlubokou fyzikální analýzou.) Prostoročas může být v okolí libovolné události pokryt čtveřicí souřadnic x . Nejdůležitější teorie prostoročasu předpokládají, že element vlastního času dτ (tj. délky křivky xⁱ(s) ) může být vyjádřen jako

Vzhledem k nezávislosti dτ na souřadnicích jsou g_ik = g_ki komponentami jistého tenzorového pole, které obecně závisí na souřadnicích.

Jak známo z algebry, může být matice g_ik v daném bodě uvedena na diagonální tvar. Aby diagonální komponenty odrážely ekvivalenci tří prostorových směrů, a jejich odlišnost od směru časového, přicházejí v úvahu možnosti

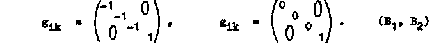
Uveďme zde, že zvláště v souvislosti se snahami o sjednocení interakcí se dnes studují i teorie s vícerozměrným kontinuem (s rozměrem 5, 7, 11), v němž může být popřípadě i vícerozměrný čas. Fyzikální interpretace dalších dimenzí je ovšem dosud ne zcela jasná /10/.

Případ (B₁) odpovídá teorii relativity. V tomto případě, doplníme-li v (A) pod odmocninou znak absolutní hodnoty, můžeme podle daného vztahu počítat i prostorové vzdálenosti. Dochází tak k nerozlučnému spojení prostorových a časových vzdáleností, které zdůrazňoval H. Minkowski /7/. (Zejména v astronomickém měřítku je i prakticky vhodné měřit prostorové vzdálenosti časem, jak ukazuje už název „světelný rok“.) Veličiny g_ik nazýváme v tomto případě složkami metrického pole a mluvíme o riemannovské (přesněji pseudoriemannovské) geometrii prostoročasu. Ve speciální teorii relativity lze dát složkám g_ik tvar (B₁) v celém prostoročase. V učebnicích se podrobně ukazuje, jak tento tvar vede k relativitě současnosti, dilataci času, existenci mezní rychlosti nezávislé na volbě vztažného systému apod.

Podle obecné relativity jsou veličiny g_ik v gravitačním poli nutně závislé na souřadnicích. V jistém okolí však lze vždy zavést synchronní systém, v němž platí

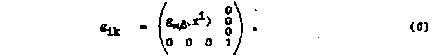
Je to umožněno tím, že čtyřmi transformacemi souřadnic lze dát čtyřem komponentám g_ik předem zadané hodnoty. Z geometrického hlediska znamená synchronní systém kolmost „hyperploch současnosti“ τ = konst na světočáry vztažného systému x^α = konst.

Dodejme ještě, že v obecné teorii relativity se setkáváme s případy, kdy délky některých (popř. všech) světočar jsou v jednom (popř. v obou) směrech konečné a nelze je dále prodloužit. Ani nekonečnost tedy není apriorní vlastností času.

Newtonovské fyzice odpovídají komponenty g_ik tvaru

kde T je Newtonův absolutní čas. Zvolíme-li T za čtvrtou souřadnici, dostáváme zřejmé (B₂), přičemž τ = t = T . Zde vlastní čas splývá se souřadnicovým a je navíc synchronizován. V tomto případě ovšem (A) neumožňuje počítat prostorové vzdálenosti a spojení prostoru s časem je proto méně těsné.

Myslím, že zde nastíněné myšlenky a poznatky by měly mít místo ve studiu každého posluchače vysokoškolské fyziky (i učitelské). Poskytuji sjednocující pohled na zdánlivě odtržené oblasti fyziky, pomáhají oprostit se od apriorních dogmat a „samozřejmostí“ a rozvíjejí tak studentovu fyzikální kulturu bez ohledu na to, že jich snad ve své práci přímo nepoužije. Jako dílo geniálních tvůrců mají také velkou hodnotu filozofickou a estetickou.

O zbývajících aspektech času se zmíníme jen stručně.

3. Šipka času

Na obtížnost sloučení mechanicko-geometrického pojetí času s jeho vývojovými aspekty poukazovali zejména filozofové, ale i řada fyziků jako např. Eddington /11/ a v současné době Prigogine /12/. Je nepochybné, že pochopení původu „směru času“ by přispělo k sblížení věd o živé a neživé přírodě a k vysvětlení kontrastu mezi neměnností přírodních zákonů a vývojem, který vytváří nové kvality. I porovnání názorů nejvyšších autorit (např. /13, 14, 15/) naznačuje, že je to problém otevřený a fascinující již tím, jak překračuje hranice specializací i vědních oborů. Myslím však, že vědomí existence otevřených problémů je pro studenty neméně cenné jako „pozitivní“ poznatky. Problém směru času může být dobrou příležitostí, jak toto vědomí rozvíjet, což ovšem vyžaduje hluboké a všestranné vzdělání a neustále obnovovaný kontakt s novými myšlenkami ze strany pedagoga.

4. Přítomnost

Poslední aspekt je v čistě vědeckých diskusích zpravidla opomíjen. Tím více však zasahuje naše úvahy o tom, co vědecké poznání lidstvu nakonec přinese. Mluvíme-li např. o odpovědnosti vědců, vyhýbáme se zpravidla otázce, co znamená slovo „odpovědnost“ v čistě přírodovědeckém obraze světa. Obyvatel planety Tralfamadore v románu K. Vonneguta, který vnímá čas „vědecky“, říká /16/:

„Pozemšťané velice rádi všechno vysvětlují. Vysvětlují, proč tato událost probíhá právě takto a ne jinak. Říkají, jak je možno další události způsobit anebo se jim vyhnout. Jsem Tralfamadořan, vidím čas jako celek, tak jako vy vidíte hřeben Skalistých hor. Celý čas je celý čas. Nemění se. Nelze před ním varovat ani jej vysvětlit. Prostě je. Rozeberte si to okamžik po okamžiku a zjistíte, že jsme všichni, jak jsem už řekl, brouci v jantaru.“

Tralfamadořany proto netíží, že vesmír bude zničen (z hlediska pozemšťanovy interpretace) při jejich nezdařeném experimentu, anebo že v jejich historii se vyskytují období válek stejně krutých jako na Zemi. „Jsme proti nim bezmocni, tak se na ně prostě nedíváme.“

Myslím, že „tralfamadorská“ povaha času dobře zapadá do obrazu Newtonovy fyziky, který byl podán na našem semináři /17/. Teorie relativity těsnějším spojením prostoru a času tuto stránku ještě zvýraznila, což našlo odraz i v Einsteinově filozofii /18/. Naproti tomu kvantová teorie vnáší do našich představ nový aspekt, který se projevuje v debatách o procesu měření a úloze pozorovatele, započatých N. Bohrem /19, 20/. Tyto úvahy však dosud nevedly k závěrům, které by nám mohly v našem „lidském“ chápáni času pomoci, Nepomohlo by nám chápání tralfamadorské? Člověk sice nemůže nazírat čas vcelku jako hřeben Skalistých hor a uchylovat se před přítomností, do jeho idyličtějších oblastí. Ale představa, že je v něm přesto uložen jako brouk v jantaru, by mu mohla být útěchou (Tralfamadore lze chápat jako vizi válečného zajatce, který přežil bombardování Drážďan) a život odpovídající této představě by ho uchránil od mnoha vnitřních i vnějších konfliktů. Přesto takovou představu jako vodítko pro svůj život přijmout nemohu – a jedině tímto subjektivním výrokem jsem schopen ukončit debatu o aspektu (4).

Literatura

1. Dialogy 4, str. 286.

2. Kopczynski W., Trautman A.: Czasoprzestreń i grawitacja. PWN, Warszawa 1981. Kap. XT.

3. Weyl H.: Raum-Zeit-Materie. J. Springer, Berlin 1923.

4. Milna E. A.: Relativity, Gravitation and World Structure. Oxford 1935.

5. Vremja i sovremennaja fizika. Sborník. Mir, Moskva 1965.

6. Marcke R., Wheeler J.: Gravitacija kak georaetrija. In: Gravitacija i otnositelnost, ed. H. Chiu and W. W. Hoffmann. Mir, Moskva 1965.

7. Princip otnositelnosti. Sborník klasických prací. Atomizdat, Moskva 1973.

8. Landau L. D., Lifšic E. M.: Teorija polja. Nauka, Moskva 1973. Kap. I, X.

9. Syge J. L.: Relativity: the special theory. North-Holland P. C., Amsterdam 1956. Kap. I.

10. Vladimirov J. S.: Sistemy otsčeta v teorii gravitacii. Energoizdat, Moskva 1982. Část IV.

11. Eddington A..: The nature of the physical world. London 1948.

12. Prigogine I.: Ot suščestvujuščego k voznikajusčemu. Nauka, Moskva 1985.

13. Landau L. D., Lifšic E. M.s Statističeskaja fizika. Nauka, Moskva 1964. Kap. I.

14. Penrose R.: Singuljarnosti i asymetrija vo vremeni. In: Obščaja teoriia otnositelnosti, ed. S. Hawking and W. Israel. Mir, Moskva 1983.

15. Zeldovič J. B., Novikov I. B.: Strojenije i evoljucija Vselennoj, Nauka, Moskva 1975. Kap. 23, § 14, 20.

16. Vonnegut K.: Bitúnok č. 5. Bratislava 1973. Str. 69, 92.

17. Horský Z.: Janusovská tvář Newtonovy fyziky. In: (a) Pocta Newtonovi. OS Pedagogická fyzika FTS JCSMP a katedry fyziky UJEP, Brno 1986. (b) Dialogy 5.

18. Einstein A.: Sobranije naučných trudov 17. Nauka, Moskva 1967. Str. 103.

19. Bohr N.: Izbrannyje naučnyje trudy II. Nauka, Moskva 1971. Str. 398, 495, 513 aj.

20. Davies P.: Slučajnaja Vselennaja. Mir, Moskva 1985. Kap. V.

BODEHO „ZÁKON“ (1772) APOD.; ROLE OMYLŮ VE VÝUCE FYZIKY

Václav Frei

Matematicko-fyzikální fakulta UK, 121 16 Praha 2, Ke Karlovu 5

Oprávněnost hypotéz a metod užívaných ve vědecké práci lze často posoudit až dodatečně, neboť výsledek bádání nebývá předem znám. Toto zjištění je triviální, ale jeho důsledky se často nedoceňují, ve výuce i v hodnocení práce na otevřených problémech. Poukázat na tyto důsledky bylo záměrem mého příspěvku, jehož autorská charakteristika pod výše uvedeným názvem byla otištěna v Dialozích 1 (D1/96).

Příprava vlastního textu příspěvku byla pro mne poučná. Díky několika soukromým sdělením /1/ a publikovaným pramenům /2-5/ musím konstatovat, že formule uváděná někdy v literatuře jako Bodeho zákon není typickým případem (ctihodného) vědeckého omylu, který později upadl v zapomenutí. Kromě toho vlastním původcem oné formule nebyl slavný německý astronom Johann Elert Bode (1747 – 1826), nýbrž méně známý Johann Daniel Titius z Wittenbergu (1729 – 1796), který jej publikoval již r. 1766. Faktická stránka příkladu, který jsem pro svůj hlavní záměr zvolil jako ilustraci, zasluhuje tedy korektur; tím se poněkud mění i závěry, jež tu lze z historie fyziky vyvodit. Poněkud!

Titiova-Bodeova formule pro vzdálenost planet od Slunce by v astronomických jednotkách znělá

r_n = 10⁻¹ (4 + 3 ∙ 2ⁿ) ,

přičemž n nabývá pro tehdy známé planety Merkur, Venuši, Zemi, Mars, Jupiter a Saturn po řadě hodnot − ∞ , 0, 1, 2, 4, 5. Žádné fyzikální zdůvodnění nebylo k dispozici, zato velkou roli sehrála subjektivní víra autorů ve význam celých čísel v zákonech přírody. Shoda hodnot r se skutečností byla ovšem jen přibližná. Navíc v posloupnosti pořadových čísel planet chybí 3.

Nabízí se nápadná obdoba s formulí pro vlnové délky spektrálních čar atomu vodíku, jak ji „odvodil“ či spíše vypozoroval r. 1885 švýcarský učitel Johann Jakob Balmer (1825 – 1898). Také jeho vedlo silné apriorní přesvědčení o významu celých čísel. Jak známo, fyzikální vysvětlení Balmerovy formule přinesla teprve v našem století kvantová mechanika. A Balmer vyšel pouze ze čtyř(!) tehdy známých hodnot λ ; později nalezené a proměřené spektrální čáry potvrzují jeho formuli s vysokou přesností.

Balmerův nepředvídatelný úspěch pokládám za cenné poučení, pokud jde o hodnocení snah vedených i málo racionálními předpoklady. Choulostivá je otázka, kdy už je záhodno nebo nutno opustit předpoklad, jemuž příroda zapravdu nedává. Dějiny fyziky takové případy znají: tepelné fluidum, ... Pro adekvátní pochopení fyziky (a vědy vůbec) jako lidského díla poskytují k „balmerovskému optimismu“ důležitý korektiv – stává se (a jak často!), že postup třeba i po všech stránkách korektní vede k zápornému výsledku. Je pak věcí vědecké pokory a lidské solidnosti tento závěr přijmout, což je obdobné jako fair play ve sportu, ale v důsledcích často závažnější.

Musím upřesnit, že případ Titiovy-Bodeovy formule není k historické ilustraci takového korektivu tak vhodný, jak jsem se domníval v D1/96 na základě svých poznámek z četby /2/. Formule se osvědčila při objevu planetky Ceres (n = 3) i Uranu (n = 6). Přes nezdar s Neptunem a Plutém neupadla v zapomenutí, nýbrž byla a je dosud různě vylepšována, poměrně úspěšně aplikována i na družice velkých planet, a co víc, probíhají a zčásti se daří seriózní pokusy zákonitost v posloupnosti hodnot r fyzikálně vysvětlit /3, 4, 5/, např. studiem vzniku planetární soustavy z plynného nebo mlhovinového útvaru. Snad lze závěrem říci, že Titius a Bode postřehli a zárodečně formulovali reálnou zákonitost, která dlouho vypadala mysteriózně a zdála se potvrzovat např. pythagorejské nauky o vládě čísel v přírodě, nakonec však připouští kauzální vysvětlení, dokonce v rámci již známých zákonitostí (gravitačního zákona, zákonů hydrodynamiky atp.). Samozřejmě nepominutelným kritériem pro potvrzení existence i pro vědecky uspokojivé vysvětlení takové zprvu jen tušené zákonitosti zůstává pozorování a experiment.

Literatura

1. Zejména mi pomohli P. Andrle a Z. Horský z Astronomického ústavu ČSAV v Praze.

2. Holton G., Brush S. G.: Introduction to Concepts and Theories in Physical Science. Princeton University Press, Princeton 1973.

3. Nieto M. M.: The Titius-Bode Law of Planetary Distances, Its History and Theory. Pergamon Press, Oxford (...) 1972.

4. Grygar J., Horský Z., Mayer P.: Vesmír. Mladá fronta, Praha 1979. Např. str. 344-345.

5. Pro ilustraci a jen namátkou uvádím, že této problematice je věnována řada článků v mezinárodním časopise The Moon and the Planets, např. v 26. svazku (1982), a v následnickém časopise Earth, Moon, and Planets, např. v 31. svazku (1984).

EURÓPSKA FYZIKÁLNA SPOLOČNOSŤ A FYZIKÁLNĚ VZDELÁVANIE

Eleonóra Adlerová

Katedra fyziky FE SVŠT, 812 19 Bratislava, Mlýnská dolina

Zatiaľ čo činnosť Európskej fyzikálnej spoločnosti (EPS) zameraná na rozvoj jednotlivých fyzikálnych odborov je širokej fyzikálnej verejnosti v ČSSR pomerne dobré známa, o aktivite EPS v oblasti fyzikálneho vzdelávania sa vie podstatné menej. Hlavným nositeľom a koordinátorom aktivity EPS v oblasti fyzikálneho vzdelávania na všetkých stupňoch školskej i postgraduálnej výchovy je Advisory Committee on Physics Education (ACPE). Náplň práce uvedeného poradného orgánu EPS je široká a rozmanitá. Cieľom tohoto príspevku je stručná informácia o aktivite a výsledkoch práce ACPE v posledných rokoch a o niektorých plánovaných akciách.

Za veľmi užitočný čin, při zrode ktorého stál ACPE, možno považovať založenie časopisu EUROPEAN JOURNAL OP PHYSICS (pôvodne s podtitulom EDUCATION). Myšlienka založil časopis určený ako platforma pre výmenu ídeí, skúseností, názorov a konkrétnych metodických postupov vo vysokoškolskej výučbe fyziky vznikla súčasné v EPS a v Institute of Physics (IoP) – asi v roku 1978. Vychádzala zo skutočnosti, že zatiaľ čo v Európe niet núdze o odborné fyzikálne časopisy, ohýbalo práve fórum, na ktorom by si vymieňali názory, nápady a skúsenosti učitelia angažovaní predovšetkým vo vysokoškolskej výučbe fyziky – či už v príprave budúcich fyzikov, učiteíov fyziky, inžinierov (resp. v akejkoľvek inej vzdelávajúcej inštitúcii zaoberajúcej sa fyzikou).

Ako oficiálny dátum založenia časopisu sa uvádza jún 1980, editorom sa stal IoP. Edičná rada sa skladá z 10 členov nominovaných EPS (na návrh ACPE) a 6 členov IoP, v prípade potreby ešte ďaľších členov kooptovaných priamo edičnou radou. Časopis by mal uverejňovať články nasledovných kategórií:

(a) články vyslovené „výučbového“ charakteru, tj. pojednávajúce o fyzikálnych témach z hľadiska metodického, články konzultačného charakteru, články o konkrétnych metódach výučby fyziky praktizovaných na rôznych vysokých školách, články o metódach výchovy budúcich učiteľov fyziky;

(b) články úvahovej, pripadne i špekulatívnej povahy poskytujúce nové pohľady na známe tematické výučbové celky;

(c) články zaoberajúce sa interdisciplinárnymi problémami fyziky a iných, najmä prírodných vied;

(d) časopis by mal tiež príležitostne poskytovať priestor na diskusiu o príspevku fyziky k celkovej kultúre osobnosti.

Prvé čísla časopisu vyšli v r. 1980. Aj keď skúsenosti prvých rokov ukazovali na neochotu (alebo prílišnú skromnosť?) vysokoškolských učiteľov zdielať svoje problémy a skúsenosti z výučby fyziky písomnou formou na stránkach EJP, resp. čiastočne i na nepochopenie zamerania časopisu, dnes je už situácia stabilizovaná po všetkých stránkach. Preferovaným jazykom časopisu je prirodzene angličtina, objavujú sa však i články v inom európskom jazyku.

ACPE nestál len pri zrode časopisu, jeho trvalou úlohou je gestorstvo odbornej náplně časopisu, navrhovanie členov edičnej rady. Editor časopisu pravidelné referuje na zasadaniach ACPE o všetkých problémoch spojených s vydávaním časopisu.

Pokiaľ ide o našu účast na vydávaní tohoto iste veľmi užitočného časopisu, potešiteľné je to, že už v prvej edičnej rade sme mali zastúpenie prof. Pišútom z Matematicko-fyzikálnej fakulty Univerzity Komenského. Je iste ocenením kvality jeho práce skutočnosť, že v r. 1985 prevzal funkciu editora, ktorú dovtedy vykonával prof. Series z Reading University. K zlepšeniu nášho postoja k tomuto časopisu a iste i ku skvalitneniu výučby fyziky by výrazné přispěli dve veci: (1) ponuka ďaľších príspevkov na opublikovanie a (2) získanie časopisu predplatiteľskou formou aspoň na vybrané pracoviská vysokých škôl. To druhé je nádejné až po vytvorení možnosti platiť časopis v domácej mene.

Trvalým sprievodcom aktivity ACPE od jeho založenia je neperiodický bulletin EUROPHYSICS EDUCATION NEWS, ktorý vychádza za čiastočnej podpory UNESCO (finančnej i distribučnej). Jeho editorom je prof. Janner (Univerzita v Nijmegen, NL). V jeho doterajších číslach sa vystriedali informatívne články o výučbe fyziky na rôznych typoch škôl vo viacerých európskych krajinách, o práci vo fyzikálnom laboratóriu, o metódach inovácie výučby fyziky a i. Jedno z čísel podáva prehľad o obsahu, rozsahu, zaradení fyziky na školách 2. stupňa v 20 európskych krajinách. V poslednom čísle sa diskutujú problémy spojené so zavádzaním výpočtovej techniky do výučby fyziky. Cesta pre nové príspevky je aj tu otvorená.

Ďaľšou oblasťou, v ktorej ACPE ako hlavný gestor vyvíja aktivitu v poslednom čase, je program krátkodobej výmeny vysokoškolských učiteľov fyziky „TEACHING ABROAD“. Cieľom tohoto programu, ktorý odštartoval v šk. roku 1980/81, je sprostredkovať výmenu vysokoškolských učiteľov fyziky medzi krajinami, ktorých národné spoločnosti sú členmi EPS, pričom hlavná aktivita hosťujúceho učiteľa má byl zameraná na vyučovanie fyziky v najnižších ročníkoch (undergraduate level). Vítaná je napr. aktivita v oblasti demonštrovania základných fyzikálnych javov, prípravy nových laboratórnych úloh a pod.

Snahou EPS je získať pre tento projekt hostiteľské pracoviská a doporučovať renomovaných učiteľov fyziky. Zatiaľ sa ukázala ako najaktívnejšia Univerzita v Lunde (Švédsko), na ktorej strávili dvojmesačný pobyt prof. Kaczmarek z PĽR (1983) a prof. Luchner z NSR (1985). Pre práve začatý šk. rok prišla opät ponuka z Lundu (na 2-4 mesiace), ktorá bola postúpená obidvom fyzikálnym vedeckým sekciam. Podrobnosti o programe TA boli uverejnené v bulletinu EPS EUROPHYSICS NEWS (júl-august 1980).

Neposlednou oblasťou v činnosti ACPE je účasť na príprave generálnych konferencií EPS, ktoré sa konajú v pravidelných trojročných intervaloch. Od roku 1978, kedy na 4. generálnej konferencii EPS v Yorku (GB) odznela v rámci plenárnych zasadaní popri vysoko odborných fyzikálnych prednáškach po prvýkrát aj prednáška s pedagogickým zameraním („Vyučovanie fyziky a Piaget“) a kedy sa (v rámci sekcie Fyzika a spoločnosť) prezentovali aj príspevky zamerané na výučbu fyziky na vysokých školách, stalo sa dobrou tradíciou venovať otázkam fyzikálnej výchovy jednu pozvanú plenárnu prednášku a minimálne poldňové sympózium na každej z nasledujúcich generálnych konferencií.

Voľba témy plenárnej prednášky, výber vhodného rečníka a kompletná príprava pedagogických sympózií je jednou z úloh ACPE. V Istanbule to bola prednáška prof. Sexla (Rakúsko) na tému „Fyzika ako výchovný prostriedok“ a sympózium venované európskym trendom vo výučbe fyziky na základných a stredných školách – doplnené malou výstavkou učebníc. V Prahe 1984 odznela zaujímavá prednáška prof. Marxa (MLR) „Čo je fyzika?“. Bohatá účasť na dvoch sympóziach zameraných na rôzne aspekty fyzikálnej výchovy v širšom slova zmysle, resp. na obraz fyziky v povedomí verejnosti (spoluorganizátor ACPE) bola dôkazom, že tieto problémy nenechávajú ľahostajnými ani značnú časť fyzikov v neučiteľských postoch.

V súčasnosti sa ACPE pripravuje na 7. generálnu konferenciu EPS, ktorá bude v auguste budúceho roku v Helsinkách. Ako pozvaný prednášateľ by sa na plenárnom zasadaní mal objaviť prof. Pippard z Cambridge University s témou „Výučba fyziky na univerzitnej úrovni a jej implikácia na školách“. Pre sympózia bola zvolená téma „Výsledky výskumu v oblasti fyzikálneho vzdelávania a ich využitie vo výučbe fyziky“.

Uvedeným výčtom prirodzene činnosť ACPE nekončí. Je potrebné spomenúť ešte aspoň snahy o vytvorenie európskeho centra zameraného na výučbu, ktoré postupne prerástli v reálnejší program organizovania siete letných škôl a seminárov o problémoch výučby fyziky (napr. Klagenfurt 1985, ČSSR 1988(?)), pokusy o zmapovanie výučby v terciárnej sfére (neúspešné), pokusy získať a publikovať prehľad o cenách a vyznamenaniach udeľovaných v európskych krajinách za výsledky v oblasti výučby fyziky, sledovanie medzinárodných fyzikálnych olympiád a pod.

V poslednom čase ACPE venuje značnú pozornosť zlepšeniu spolupráce s ďaľšími medzinárodnými orgánmi zaoberajúcimi sa fyzikálnou výchovou, menovite s ICPE (International Commission for Physics Education – IUPAP), GIREP (Groupe Internationale de Recherche sur 1'Enseignement de la Physique) a AAPT (American Association of Physics Teachers). Spolupráca s UNESCO má v EPS už tradíciu.