Subsections
Mezní chyba 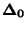 měřicího přístroje je jeho nejvyšší přípustná chyba,
kterou ostatní odchylky přístroje za daných podmínek nepřekročí.
Redukovaná mezní chyba
měřicího přístroje je jeho nejvyšší přípustná chyba,
kterou ostatní odchylky přístroje za daných podmínek nepřekročí.
Redukovaná mezní chyba
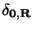 měřicího přístroje pro určitou
hodnotu hodnotu měřené veličiny
měřicího přístroje pro určitou
hodnotu hodnotu měřené veličiny 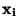 a stanovené podmínky je dána poměrem
mezní chyby
a stanovené podmínky je dána poměrem
mezní chyby 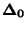 a měřicího rozsahu
a měřicího rozsahu 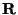 ,
,
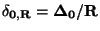 . Často se redukovaná mezní chyba udává
v procentech měřicího rozsahu
. Často se redukovaná mezní chyba udává
v procentech měřicího rozsahu 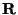 ,
,
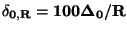 .
Měřicí rozsah
.
Měřicí rozsah 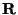 je algebraický rozdíl krajních hodnot stupnice,
je algebraický rozdíl krajních hodnot stupnice,
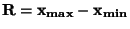 .
Třída přesnosti měřicího přístroje je klasifikačním znakem přesnosti
v celém měřicím rozsahu přístroje. Třída přesnosti se vyjadřuje kladným
bezrozměrným číslem ze stanovené číselné řady. Toto číslo je vždy větší,
nebo nanejvýš stejné, jako největší absolutní hodnota z redukovaných mezních
chyb, zjištěných za daných podmínek v celém měřicím rozsahu přístroje.
.
Třída přesnosti měřicího přístroje je klasifikačním znakem přesnosti
v celém měřicím rozsahu přístroje. Třída přesnosti se vyjadřuje kladným
bezrozměrným číslem ze stanovené číselné řady. Toto číslo je vždy větší,
nebo nanejvýš stejné, jako největší absolutní hodnota z redukovaných mezních
chyb, zjištěných za daných podmínek v celém měřicím rozsahu přístroje.
- V případě čistě aditivních chyb měření se užívá
redukovaná relativní odchylka (zde rovna třídě přesnosti přístroje)
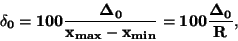 |
(90) |
kde 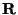 je rozmezí stupnice. U přístrojů, kde působí chyby měření aditivně,
klesá relativní odchylka
je rozmezí stupnice. U přístrojů, kde působí chyby měření aditivně,
klesá relativní odchylka 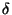 hyperbolicky s hodnotou
hyperbolicky s hodnotou 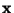 .
.
Aditivní chyby měřicího přístroje omezují rozsah použití přístroje v oblasti
malých hodnot vstupní veličiny 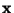 .
.
- V případě čistě multiplikativních chyb měření je relativní chyba
citlivosti (zde přímo třída přenosti přístroje)
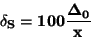 |
(91) |
konstantní. To obvykle platí jenom v omezeném intervalu, uváděném na přístroji
výrobcem.
- U kombinovaný chyb měření lze celkovou chybu rozepsat jako
součet aditivní
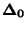 a multiplikativní
a multiplikativní
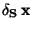 složky
podle rovnice
složky
podle rovnice
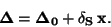 |
(92) |
Celková redukovaná relativní chyba
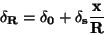 |
(93) |
pak monotónně roste s růstem 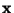 .
K vyjádření třídy přesnosti
.
K vyjádření třídy přesnosti 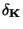 se v těchto případech užívají dva
údaje: redukovaná relativní chyba
se v těchto případech užívají dva
údaje: redukovaná relativní chyba 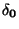 a chyba vzniklá na horní
hranici měřicího rozsahu
a chyba vzniklá na horní
hranici měřicího rozsahu 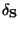 .
.
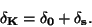 |
(94) |
=1.00mm
![\begin{picture}(150.67,100.00)\begingroup
\par\dimen0 = 9.67pt
\advance \dime...
...c]{$y_{norn}$}}
\put(137.67,67.00){\makebox(0,0)[cc]{$y_{norn}$}}
\end{picture}](img457.png)
Pro zařazení měřicího přístroje do některé z tříd přesnosti je rozhodující
největší hodnota redukované mezní chyby zjištěná v celém měřicím rozsahu.
Největší mezní chyba nesmí překročit při zvolené třídě přesnosti 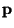 hodnotu
hodnotu
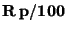 . Třída přesnosti se neoznačuje znaménkem, protože
redukovaná mezní chyba může být se stejnou pravděpodobností kladná či záporná.
Skutečná hodnota měřené veličiny
. Třída přesnosti se neoznačuje znaménkem, protože
redukovaná mezní chyba může být se stejnou pravděpodobností kladná či záporná.
Skutečná hodnota měřené veličiny 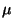 bude potom ležet v intervalu
bude potom ležet v intervalu
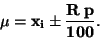 |
(95) |
Přístroje se podle třídy přesnosti třídí do řady 6 %, 4 %, 2.5 %, 1.5 %,
1.0 %, 0.5 %, 0.2 %, 0.1 %, 0.05 %, 0.02 %, 0.01 %, 0.005 %, 0.002 %,
0.001 %, doplněné o značku typu chyby 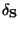 (multiplikativní),
(multiplikativní),
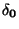 (aditivní) nebo
(aditivní) nebo
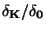 kombinované podle
následujícího schématu:
kombinované podle
následujícího schématu:
- Pro čistě aditivní chyby je třída přesnosti vyjádřena redukovanou
relativní chybou
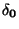 , kde
, kde 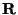 je maximum stupnice, např.
je maximum stupnice, např.
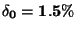 se zapíše 1.5.
se zapíše 1.5.
- U přístrojů se silně nerovnoměrnou stupnicí se uvádí třída přesnosti
formou zatrženého čísla a rozsahem stupnice
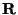 .
.
- Pro čistě multiplikativní chyby je třída přesnosti vyjádřena chybou
citlivosti
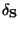 a udává se číslem v kroužku, například
a udává se číslem v kroužku, například
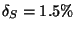 se zapíše
se zapíše
=1mm
![\begin{picture}(11.16,10.50)
\put(5.67,5.00){\circle{8.00}}
\put(5.67,5.00){\makebox(0,0)[cc]{1.5}}
\end{picture}](img464.png)
|
- Pro případ simultánního působení aditivních a multiplikativních
chyb se třída přesnosti uvádí ve tvaru zlomku
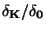 .
Zápis 1.5/1 tedy vyjadřuje
.
Zápis 1.5/1 tedy vyjadřuje
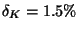 a
a
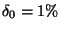 .
.
| Druh chyby |
Označení |
Rozsah |
Relativní |
Absolutní |
| |
třídy přesnosti |
stupnice 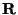 |
chyba 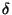 (%) (%) |
chyba 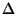 |
| |
|
|
|
|
| Aditivní |
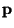 |
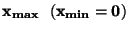 |
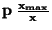 |
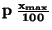 |
| |
|
|
|
|
| |
=1.00mm
![\begin{picture}(12.35,9.33)
\put(2.00,9.33){\line(1,-1){6.67}}
\put(8.33,6.00){\makebox(0,0)[lc]{p}}
\put(8.67,2.64){\line(6,5){3.68}}
\end{picture}](img471.png)
|
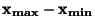 |
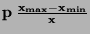 |
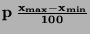 |
| |
|
|
|
|
| Multiplikativní |
=1mm
![\begin{picture}(11.16,10.50)
\put(5.67,5.00){\circle{8.00}}
\put(5.67,5.00){\makebox(0,0)[cc]{p}}
\end{picture}](img475.png)
|
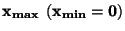 |
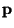 |
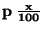 |
| |
|
|
|
|
| Smíšené |
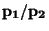 |
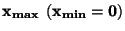 |
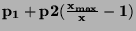 |
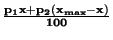 |
| |
|
|
|
|
Při výpočtech mezní chyby měřícího přístroje se podle ![$[6]$](img178.png) užívá následujícího
zaokrouhlování:
užívá následujícího
zaokrouhlování:
- Pokud je první významná číslice jednička nebo dvojka, vyjadřuje se
chyba měření prvními dvěma významnými číslicemi
- Pokud je první významná číslice trojka nebo vyšší, užívá se pouze
tato číslice
Výsledek měření se zaokrouhluje na stejný počet desetinných míst, jako má
absolutní mezní chyba přístroje.
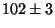 mV
mV
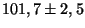 mV
mV
ppm - jedna miliontina
MH - měřená hodnota
MHMR - maximální hodnota měřícího rozsahu
(většinou odpovídá délce stupnice)
dig - číslice
- u ručkových přístrojů je uvedena třída přesnosti (například:
0,5 )
- 0,001 % MH + 0,01 % MHMR
- 50 ppm MH + 20 ppm MHMR
- 5 % MH + 20 dig
- 5 % + 20 dig
- 1 % + 0,003
- 2 % č.h + 1 dig
- 0,05 % of Reading + 0,02 % Full Scale
- 0.1 % of rdg + 5 dgt
- 0.0020 % of reading + 0.0006 % of range
Výpočtem získáme krajní chybu. To znamená, že výsledkem měření je
interval, ve kterém s 99,7 % pravděpodobností leží skutečná hodnota
měřené veličiny.
Obrázek:
Závislost velikosti relativní chyby na velikosti měřeného napětí
pro voltmetr M1T 330 (od 300 mV do 3 V) a multimetr M1T 380 (od 150 mV do 1.5 V)
|
|
Ampérmetr má třídu přesnosti 0,5
Zvolený rozsah je 1,2 A
Ručička ukazuje 0.845A
Chyba je
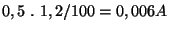 tj. 0,7 %
tj. 0,7 %
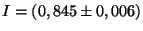 A
A
Na rozsahu 4 V je chyba 0.3 % č.h. + 1 dig.
Přístroj ukazuje 3,912 V
Chyba je
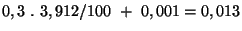 V
V
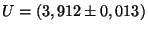 V
V
Na rozsahu 4 V je chyba 0.5 % č.h. + 2 dig.
Přístroj ukazuje 3,912 V
Chyba je
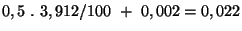 V
V
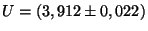 V
V
Na rozsahu 2 V je chyba 0.1 % č.h. + 5 dig.
Přístroj ukazuje 1,9123 V
Chyba je
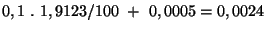 V
V
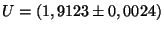 V
V
Na rozsahu 300 mV je chyba 0,01 % MH + 0,01 % MHMR
Přístroj ukazuje 284,56 mV
Chyba je
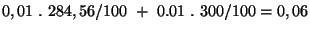 mV,
což je 0,021 %.
Stejná hodnota chyby v % se zobrazí na displeji po stlačení tlačítka
CHYBA na voltmetru.
mV,
což je 0,021 %.
Stejná hodnota chyby v % se zobrazí na displeji po stlačení tlačítka
CHYBA na voltmetru.
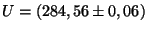 mV
mV
Pro měření stejnosměrného napětí je uvedena chyba:
50 ppm MH + 20 ppm MHMR
Rozsah je 15 V
Přístroj ukazuje 14,2338 V
Chyba je
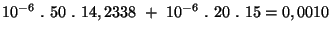 V
V
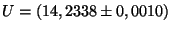 V
V
Při měření kapacity kondenzátoru ukazuje přístroj hodnotu C = 67,82 nF
Zvolený rozsah je 100 nF
Chyba přístroje uvedená v manuálu je
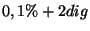
Chyba měřené hodnoty je
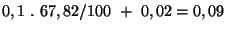 nF
nF
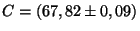 nF.
nF.
© František Šťastný, 1997
![]() měřicího přístroje je jeho nejvyšší přípustná chyba,
kterou ostatní odchylky přístroje za daných podmínek nepřekročí.
Redukovaná mezní chyba
měřicího přístroje je jeho nejvyšší přípustná chyba,
kterou ostatní odchylky přístroje za daných podmínek nepřekročí.
Redukovaná mezní chyba
![]() měřicího přístroje pro určitou
hodnotu hodnotu měřené veličiny
měřicího přístroje pro určitou
hodnotu hodnotu měřené veličiny ![]() a stanovené podmínky je dána poměrem
mezní chyby
a stanovené podmínky je dána poměrem
mezní chyby ![]() a měřicího rozsahu
a měřicího rozsahu ![]() ,
,
![]() . Často se redukovaná mezní chyba udává
v procentech měřicího rozsahu
. Často se redukovaná mezní chyba udává
v procentech měřicího rozsahu ![]() ,
,
![]() .
Měřicí rozsah
.
Měřicí rozsah ![]() je algebraický rozdíl krajních hodnot stupnice,
je algebraický rozdíl krajních hodnot stupnice,
![]() .
Třída přesnosti měřicího přístroje je klasifikačním znakem přesnosti
v celém měřicím rozsahu přístroje. Třída přesnosti se vyjadřuje kladným
bezrozměrným číslem ze stanovené číselné řady. Toto číslo je vždy větší,
nebo nanejvýš stejné, jako největší absolutní hodnota z redukovaných mezních
chyb, zjištěných za daných podmínek v celém měřicím rozsahu přístroje.
.
Třída přesnosti měřicího přístroje je klasifikačním znakem přesnosti
v celém měřicím rozsahu přístroje. Třída přesnosti se vyjadřuje kladným
bezrozměrným číslem ze stanovené číselné řady. Toto číslo je vždy větší,
nebo nanejvýš stejné, jako největší absolutní hodnota z redukovaných mezních
chyb, zjištěných za daných podmínek v celém měřicím rozsahu přístroje.
![\begin{picture}(150.67,100.00)\begingroup
\par\dimen0 = 9.67pt
\advance \dime...
...c]{$y_{norn}$}}
\put(137.67,67.00){\makebox(0,0)[cc]{$y_{norn}$}}
\end{picture}](img457.png)
![]() užívá následujícího
zaokrouhlování:
užívá následujícího
zaokrouhlování:
![\includegraphics[height=10cm, width=\textwidth, keepaspectratio=false]{m1t330}](img483.png)
![]() tj. 0,7 %
tj. 0,7 %
![]() A
A
![]() V
V
![]() V
V
![]() V
V
![]() V
V
![]() V
V
![]() V
V
![]() mV,
což je 0,021 %.
Stejná hodnota chyby v % se zobrazí na displeji po stlačení tlačítka
CHYBA na voltmetru.
mV,
což je 0,021 %.
Stejná hodnota chyby v % se zobrazí na displeji po stlačení tlačítka
CHYBA na voltmetru.
![]() mV
mV
![]() V
V
![]() V
V
![]()
![]() nF
nF
![]() nF.
nF.