Pracovní listy pro fyziku na ZŠ

Jednou z metod vědeckého zkoumání je idealizace. Při idealizaci je reálný objekt zaměněný idealizovaným za účelem snazšího poznání a formulování zákonitostí v jednodušší formě. Idealizace je kombinace elementárních postupů zkoumání - abstrakce a syntézy. Na jedné straně abstrahujeme od některých vlastností reálných objektů a procesů a na druhé straně přiřazujeme ideálnímu objektu nebo procesu takové vlastnosti, které reálný objekt nebo proces úplně nemá. Idealizace fyzikální reality je nevyhnutelným krokem při poznávání fyzikální reality ve vědě, a také ve vyučovacím procesu.

Ve vyučování musíme často vědeckou idealizaci dále zjednodušovat. Tím vytváříme idealizovaný obraz reality, který nám umožňuje vyjadřovat fyzikální vztahy a závislosti v pochopitelné formě při zachování podstatných rysů problému.

Z hlediska správného porozumění je důležité, aby žák pochopil, že se idealizací např. fyzikálního procesu nedopouštíme ničeho nesprávného, ale že oproštění se od podrobností nám umožňuje hlubší pochopení zkoumaného procesu. Poznávací a didaktická hodnota idealizace bývá znehodnocena tím, že žák si nedokáže uvědomit, kde pracuje s určitým modelem a kde naopak pracuje se skutečnou fyzikální realitou, za jakých podmínek je idealizace realizována a kde jsou meze jejího použití.

Právě práce se simulačními programy představuje využití idealizací. Vhodný program umožní několik stupňů idealizace modelových objektů. Např.: je možné nastavit u součástek nezničitelnost, čímž se stávají naprosto ideální. Dalším stupněm idealizace je práce se součástkami buď bez vnitřního odporu, nebo s vnitřním odporem. Každý stupeň najde své uplatnění v jiné části výuky.

Jeden z hlavních pilířů využití spočívá v doplnění výkladu. Učitel si předem připraví příklady k probíranému tématu (výčet možných oblastí je v minulé kapitole) a svůj výklad ilustruje předvedením probíraných závislostí. Má při tom možnost celý postup rozfázovat a podle potřeby opakovat jednotlivé sekvence a tak maximálně přiblížit popisovaný jev. Žáci tak vidí na obrazovce grafické znázornění probíhajícího pokusu a mohou se rychleji naučit číst v grafech.

Další využití tohoto programu je tvorba pracovních listů. Žáci si mohou přímo probírané jevy zkoušet a procvičovat. Velkou výhodou je okamžitá zpětná vazba. Žáci ovládají tento program sami a procvičují si nabyté vědomosti. Mají možnost ovlivňovat vstupní veličiny a sledovat nastalé změny. Velkou výhodou je, že mohou pracovat samostatně, vlastním tempem a zaměřit svou pozornost k otázkám, které při výkladu dostatečně nepochopili.

Velkou oblastí použití je také tvorba elektronických podkladů samotným učitelem. Tyto učebnice jsou interaktivní, neobsahují pouze strohá data, jsou doplněna funkčními simulacemi, grafy a obrázky. Na závěr každé lekce může učitel vytvořit test, ve kterém je možnost automatického vyhodnocení.

Elektrický obvod

Úvod

V dnešní hodině se naučíme zapojit elektrický obvod.

Sestavení prvního obvodu

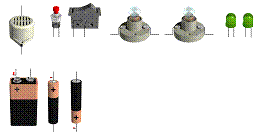
1. Sestavte z příslušných součástek, elektrický obvod, který máte v učebnici (*).

2. Sestavte další obvod z příslušných součástek, elektrický obvod, který máte v učebnici (učitel řekne konkrétní).

3. Nyníse pokuste sestavit sami nějaký jednoduchý obvod. Přemýšlejte nad tím, co je nutné k tomu, aby obvodem protékal proud.

Schématické značky

Otevřete si simulaci.

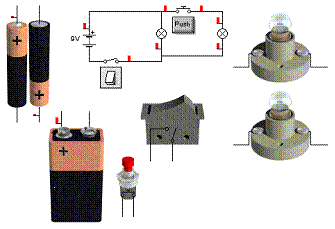
1. Sestavte podle daného schématu obvod.

2. Prochází sestaveným obvodem proud? Pokud ne, tak udělejte takovou změnu v obvodě, aby proud protékal.

3. Požádejte p. učitele o jiné schéma, které vytvoříte.

Závěr

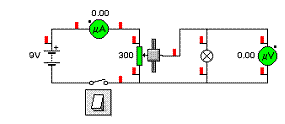
Aby obvodem protékal proud, musí obvod obsahovat zdroj elektrického napětí, spotřebič (v našem případě žárovku) a obvod musí být uzavřený. Základní schematické značky jsou značka zdroje, žárovky, vypínače.

Pracovní list

Ohmův zákon

Úvod

Elektrický proud v obvodu se dá připodobnit proudění kapaliny v uzavřeném potrubí. Pokud chceme aby potrubím protékalo větší množství vody, musíme také větší množství do potrubí dodat. U elektrického obvodu je to podobné. Vodičem protéká větší proud, jestliže se v něm pohybuje větší množství elektronů. V tomto pracovním listu se budeme zabývat závislostí proudu, který prochází vodičem, na elektrickém napětí mezi jeho konci.

Proud, napětí a odpor

Otevři si simulaci.

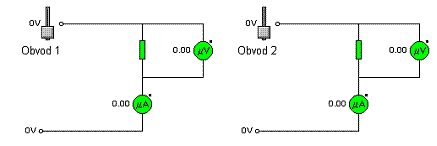
1. Pozorně se podívejte na dané obvody.

2. Nejprve se věnuj 1. obvodu. Použij jezdce ke změně napětí, pozoruj, jak se mění proud v obvodu. Jak se změní proud, jestliže zdvojnásobíš napětí? Při každé změně si zapiš hodnoty do tabulky.

3. Postup z předchozího bodu zopakuj pro 2. obvod.

4. Vidíš, že pro různá napětí jsi získal různé hodnoty proudu. S pomocí kalkulátoru si do volného pole v tabulkách spočítej podíl napětí a proudu. Jaké hodnoty ti vyšly?

5. Výsledné hodnoty porovnej s hodnotami napsanými v simulaci u rezistorů. (Hodnoty uvidíš tak, že nápisy Obvod 1 a Obvod 2 odsuneš na jiné místo.)

6. Zkus přijít na to, jaká je tedy závislost proudu na napětí. Svou hypotézu si ověř otevřením listu s názvem graf (list, ve kterém se nacházejí tabulky s hodnotami, se jmenuje Tabulky a vedle je list s názvem Graf)

Závěr

Vztah mezi proudem, napětím a odporem udává Ohmův zákon:

Elektrický proud v kovovém vodiči je přímo úměrný elektrickému napětí U mezi konci vodiče.

I =

Z grafu jednoznačně vidíme, že při větší hodnotě podílu napětí a proudu klade rezistor větší odpor průchodu proudu. Tímto podílem budeme určovat elektrický odpor, označíme ho R. Jeho jednotkou je ohm (Ω)

R =

Pracovní list

Spojení rezistorů v elektrickém obvodu za sebou

Úvod

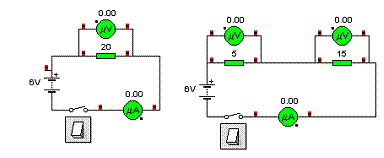V tomto pracovním listu se budeme zabývat určením výsledného odporu rezistorů spojených za sebou. Toto zapojení se nazývá sériové zapojení rezistorů. Příklad takového zapojení vidíte na obrázku. Budeme sledovat rozložení napětí na jednotlivých rezistorech a proud protékající obvodem.

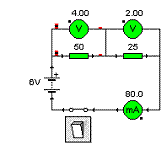
Rezistory v sérii

Otevřete si simulaci:

Důkladně si prohlédněte oba obvody. Jaké jsou velikosti odporů rezistorů?

Uzavřete levý obvod a zapište si velikost proudu, který ukazuje ampérmetr.

Jakou hodnotu proudu budete tedy očekávat, že ukáže ampérmetr po zapnutí obvodu? Větší, stejnou nebo menší? Zapněte obvod a ověřte si svou hypotézu.

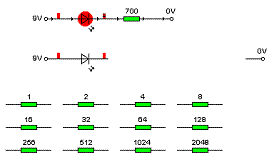Určení výsledného odporu

Otevřete si simulaci:

1. Zjistěte, jaké je na diodě napětí a jaký protéká diodou proud.

2. Bohužel nemáme žádný rezistor s hodnotou 700Ω. Máme pouze rezistory, které jsou pod obvodem. Spojte vhodnou kombinaci rezistorů do série, abyste získali rezistor o odporu co nejbližším hodnotě 700Ω.

Závěr

Výsledný odpor R spotřebičů spojených do série se rovná součtu odporů R₁…….R_n spotřebičů.

R = R₁+ R₂ + R₃+ ……………….+ R_n

Napětí U mezi vnějšími svorkami rezistorů spojených do série se rovná součtu napětí U₁……U_n mezi svorkami jednotlivých rezistorů:

U = U₁+ U₂ + U₃ + ………………..+ U_n

Všimněte si, že spotřebiči prochází stejný proud, ale na spotřebičích jsou různá napětí!

Pracovní list

Spojení rezistorů v elektrickém obvodu vedle sebe

Úvod

V tomto pracovním listu se budeme zabývat určením výsledného odporu rezistorů spojených vedle sebe. Toto zapojení se nazývá paralelní zapojení rezistorů. Příklad takového zapojení vidíte na obrázku. Budeme sledovat rozdělení proudu do jednotlivých větví obvodu a napětí na rezistorech.

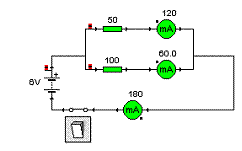
Paralelně spojené rezistory

Otevřete si simulaci:

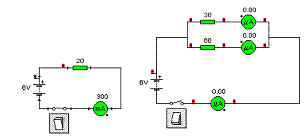
1. Důkladně si prohlédněte oba obvody. Jaké jsou velikosti odporů rezistorů?

2. Zapněte levý obvod a poznačte si hodnotu proudu, který ukazuje ampérmetr.

3. Jakou hodnotu proudu budete tedy očekávat, že ukáže ampérmetr před vypínačem po zapnutí obvodu? Větší, stejnou nebo menší? Zapněte obvod a ověřte si svou hypotézu.

Určení výsledného odporu

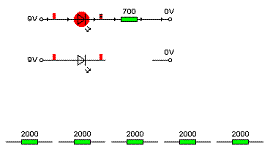Otevřete si simulaci:

1. Zjistěte, jaké je na diodě napětí a jaký jí protéká proud.

2. Bohužel nemáme žádný rezistor s hodnotou 700Ω. Máme pouze rezistory, které jsou pod obvodem. Spojte vhodnou kombinaci rezistorů paralelně, abyste získali rezistor o odporu co nejbližším hodnotě 700Ω.

3. Zapoj paralelně správný počet rezistorů. Správnost ověříš tím, že daným obvodem musí protékat proud 10 mA až 11 mA a dioda svítí plně.

Závěr

Pro výsledný odpor R spotřebičů spojených paralelně platí.

= + + + ................ +

Proud v nerozvětvené části se rovná součtu proudů ve větvích:

I = I₁ + I₂ + I₃+ ………………+I_n

Všimněte si, že spotřebiči prochází různé proudy, ale na spotřebičích je stejné napětí!

Pracovní list

Reostat

Úvod

Někdy je nutné změnit velikost napětí nebo proudu v obvodu. Často se k tomu využívá reostat. Reostat je rezistor, jehož odpor je možno měnit. Nejjednodušší provedení reostatu je, že na válec z izolantu navineme odporový drát, jehož konce jsou spojeny dvěma svorkami. Reostat má ještě třetí svorku, spojenou s jezdcem, který se posunuje po drátě rezistoru a tím mění jeho délku a tím i jeho odpor.

Užití reostatu ke změně proudu v obvodu.

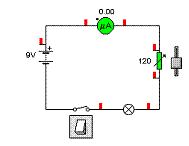Otevřete si simulaci.

Důkladně si prohlédněte schéma obvodu. Jedná se o jednoduchý obvod nebo rozvětvený?

astavte posuvný kontakt – tzv. jezdec na reostatu do takové polohy, aby po sepnutí spínače obvodem protékal maximální proud.

Svou hypotézu si ověřte sepnutím spínače. Jaká je tedy maximální hodnota proudu? Jaká je při tom hodnota odporu reostatu?

Pokud budete zvětšovat hodnotu odporu reostatu, bude klesat proud protékající obvodem. Vyzkoušejte!

Reostat jako dělič napětí (potenciometr)

Otevřete si simulaci.

Důkladně si prohlédněte schéma obvodu. Jedná se o jednoduchý obvod nebo rozvětvený? Ve které části obvodu budeme měnit napětí?

Nastavte jezdce na potenciometru do takové polohy, aby po sepnutí spínače bylo v sekundárním obvodu maximální napětí.

V místě kontaktu jezdce se odděluje z celkového napětí mezi krajními body potenciometru určitá část. Podle toho jakou část napětí potřebujeme, posuneme jezdce na příslušný konec potenciometru. Vyzkoušejte si různé polohy jezdce.

Pracovní list

Stín

Úvod

Pokud dáte např. ruku mezi stolní lampu a stůl, můžete na stole pozorovat stínový obraz své ruky. Světlo za vaši ruku neproniká. Dnes se tedy budeme zabývat tím, jaký stín vzniká za neprůsvitnými tělesy .

Jednoduchý stín

Otevřete si simulaci.

1. Simulace nám ukazuje bodový zdroj světla. Přesuňte míček do osvětlené části.

2. Představte si stín vržený míčkem. Bude mít ostrý přechod mezi osvětlenou částí a stínem, nebo budete očekávat hranici polostínu?

3. Jak by vypadaly stíny, jestliže by se světlo ohýbalo za obvyklé předměty? Co nám to tedy říká o šíření světla?

Skutečný stín

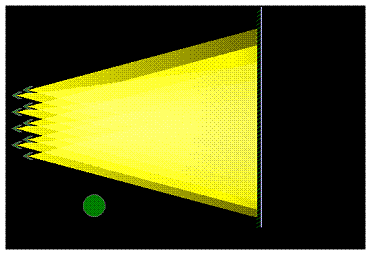Otevřete si simulaci.

1. V životě se však často s bodovými zdroji světla nesetkáváme. Setkáváme se s reálnými zdroji. Každý bod na povrchu takového reálného zdroje můžeme považovat za nový bodový zdroj.

2. Posuňte míček do cesty světelného paprsku z nebodového zdroje světla v simulaci. Jak se liší nynější stín od stínu v prvním případě, kdy jsme použili bodový zdroj světla?

3. Pokuste se popsat, co byste viděli, pokud byste byli za míčkem?

Závěr

Objekt umístěný v cestě světelného paprsku z bodového zdroje vrhá vždy plný stín s ostrými hranicemi. Z toho plyne, že se světlo šíří přímočaře a že se neohýbá za obvyklé předměty. Jestliže objekt osvítíme plošným zdrojem světla, stín bude mít tmavé centrum tzv. plný stín, který je ohraničený částečným stínem tzv. polostínem.

Pracovní list

Zatmění Slunce

Úvod

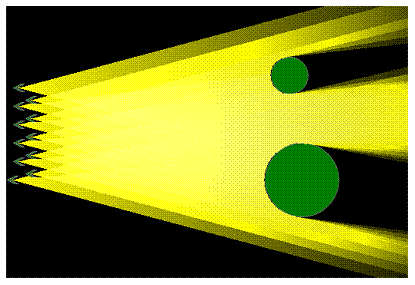
K zatmění Slunce dochází, pokud Měsíc prochází mezi Zemí a Sluncem. Část Země je v tuto dobu ve stínu měsíce.

Zatmění

Otevřete i simulaci.

1. Přesuňte menší míček (reprezentující Měsíc) před větší míček (reprezentující Zemi) tak, že se stín Měsíce právě dotýká povrchu Země. Takto to vypadá při zatmění Slunce.

2. Slunce je mnohonásobně větší než Měsíc, ale je také mnohonásobně dál, proto se ze Země jeví jejich velikost jako stejná. Proto pokud Měsíc prochází mezi Sluncem a Zemí, může na určitém bodě Země úplně pokrýt Slunce.

Druhy zatmění

Otevřete si simulaci.

1. Pečlivě se podívejte na místo, kde se dotýká stín Měsíce zemského povrchu. Co byste očekávali, že vidí lidé v tomto místě Země?

2. Co očekáváte, že uvidí pozorovatel z míst, kde je na povrchu Země polostín?

3. Zaměňte pořadí Země a Měsíce. Zamyslete se nad tím, proč jsou častěji vidět zatmění Měsíce než Slunce.

Závěr

Sluneční zatmění jsou způsobena tím, že Měsíc vrhá svůj stín na část zemského povrchu. Úplná zatmění Slunce se vyskytují v místech plného stínu. Pokud se pozorovatel nachází v místě polostínu, pozoruje částečné zatmění Slunce.

Pracovní list

Odraz světla- zákon odrazu

Úvod

Světlo se může odrážet od různých povrchů, často vidíme odraz ve vodě, nebo v okně. Plochy které dobře odrážejí světlo budeme nazývat zrcadla. Zrcadla však nemusí být pouze rovinná, mohou být také dutá, nebo vypuklá.

Odraz na rovinném zrcadle

Otevřete si simulaci:

1. Pečlivě si prohlédněte simulaci. Posuňte zdroj světla tak, aby paprsek dopadal na zrcadlo.

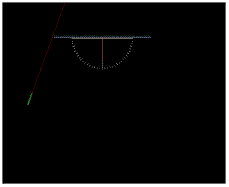
2. Nasměrujte paprsek do středu úhloměru a zaznačte si úhel dopadu a odrazu. Vyzkoušejte pro různé úhly dopadu. Hodnoty si zapište do tabulky(úhel dopadu i odrazu měříme od kolmice dopadu).

α- úhel dopadu	ά- úhel odrazu

Odraz na rovinném zrcadle 2

Otevřete si simulaci:

1. S pomocí znalosti zákona odrazu vyřešte následující problém. Přiložená zrcátka doplňte do připravené krabičky tak, aby vznikl periskop tzn. paprsky budou dopadat na zelenou kuličku. Jaký úhel svírají zrcátka? (Pozor nulový úhel je svisle vzhůru, ale zdroj v simulaci vrhá paprsky ve vodorovném směru doprava, což je v simulaci úhel 90 stupňů).

2. Pokud byste se podívali do takového periskopu, jaký obraz uvidíte? Bude převrácený vzhůru nohama? Nebo stranově převrácený?

3. Přidejte si do simulace další zrcadla a vyzkoušej další různé možné sestavy zrcadel.

Závěr

Úhel odrazu se rovná úhlu dopadu. Odražený paprsek leží v rovině dopadu.

Pracovní list

Zobrazení rovinným zrcadlem

Úvod

Jestliže se objekt odráží v rovinném zrcadle, jeho obraz je zdánlivý tzn. za zrcadlem a to ve stejné vzdálenosti, jako je objekt před zrcadlem. Tento obraz je také stranově převrácený. Jak vzniká obraz v rovinném zrcadle?

Kde je obraz?

Otevřete si simulaci.

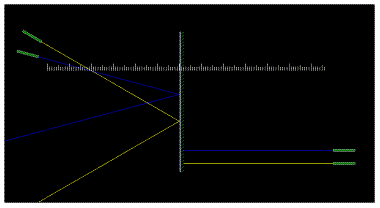
1. Bod, ve kterém se paprsky kříží reprezentuje objekt, který se nachází před zrcadlem. Posuňte a natočte zdroje světelných paprsků v pravé části tak, aby jejich paprsky navazovaly na paprsky v odražené části.

2. V bodě, kde se protínají paprsky na pravé straně, vzniká obraz původního objektu.

3. Porovnejte vzdálenost mezi objektem a zrcadlem se vzdáleností mezi obrazem a zrcadlem. Co pozorujete?

Porovnání objektu a obrazu

Otevřete si simulaci.

1. Tato simulace ukazuje obraz zdroje světla v levém horním rohu. Pozorně si prohlédněte původní objekt a jeho obraz, který se nachází v pravém horním rohu. Jak se liší z pohledu pozorovatele, který je reprezentován míčkem?

2. Dokázali byste najít takové uspořádání zrcadel, které vrátí obraz shodný s původním objektem?

Závěr

Obraz v rovinném zrcadle je zdánlivý, stejně velký jako předmět a je stranově převrácený.

Pracovní list

Dutá zrcadla

Úvod

Dalším typem zrcadla, se kterým se můžete v praxi setkat, je duté zrcadlo. Toto zrcadlo patří do skupiny kulových zrcadel. Paprsky dopadající na duté zrcadlo, které jsou rovnoběžné s osou zrcadla, se po odrazu soustředí do jednoho bodu. Paprsky vycházející z tohoto bodu se odrážejí od zrcadla tak, že jsou rovnoběžné s jeho osou.

Odraz rovnoběžných paprsků

Otevřete si simulaci.

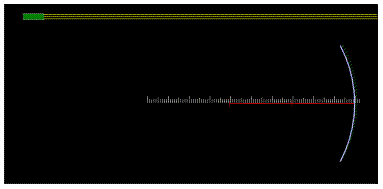
1. Červená úsečka, která je kolmá na střed zrcadla, je jeho hlavní osa. Značka na konci úsečky je střed křivosti dutého zrcadla.

2. Pohybujte zdrojem světla nahoru a dolů, je však důležité, aby paprsky byly stále rovnoběžné s osou zrcadla. Čeho jste si u paprsků odražených ze zrcadla všimli?

3. Bod, do kterého se po odrazu soustředí paprsky, budeme nazývat ohnisko. Použijte přiložené pravítko a změřte vzdálenost ohniska od středu zrcadla. Porovnejte naměřenou hodnotu se vzdáleností středu křivosti od středu zrcadla (poloměr křivosti).

4. Změňte alespoň dvakrát poloměr křivosti daného zrcadla a vždy změřte příslušnou ohniskovou vzdálenost. Zapište si hodnoty do tabulky a porovnejte je.

Poloměr křivosti	Ohnisková vzdálenost

Odraz rozbíhavých paprsků

Otevřete si simulaci.

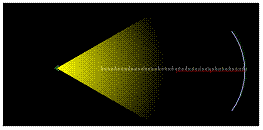
1. Posunujte zdroj světla směrem k zrcadlu. Kam sesoustředí paprsky, jestliže se zdroj nachází za středem křivosti? Co se stane, jestliže zdroj umístíme do středu křivosti?

2. Pokračujte v přibližování zdroje směrem k zrcadlu. Kam se soustředí odražené paprsky, jestliže je zdroj mezi středem křivosti a ohniskem? Co se stane, jestliže zdroj dosáhne ohniska?

3. Zkuste popřemýšlet o praktickém využití některého z uspořádání.

Závěr

Paprsky dopadající na duté zrcadlo, které jsou rovnoběžné s osou zrcadla, se po odrazu soustředí do ohniska. Ohnisková vzdálenost je jednou polovinou poloměru křivosti. Jestliže umístíme zdroj světla do ohniska dutého zrcadla, odražené paprsky jsou rovnoběžné s osou zrcadla.

Pracovní list

Vypuklá zrcadla

Úvod

Dalším typem kulových zrcadel je zrcadlo vypuklé.

Odraz ve vypuklém zrcadle

Otevřete si simulaci.

1. Posuňte zdroj tak, aby se paprsky odrážely v zrcadle. Čeho si všimnete u odražených paprsků?

2. Pohybujte zdrojem nahoru a dolů. Dokázali byste určit ohnisko zrcadla?

Ohnisková vzdálenost zrcadla

Otevřete si simulaci.

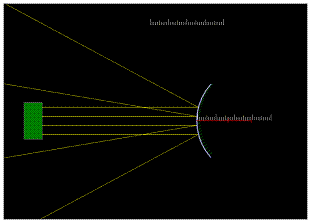
1. Posuňte a natočte pravítko umístěné v horní části simulace tak, aby bylo rovnoběžné s jedním z odražených paprsků a leželo na něm.

2. Použijte pravítko pro zjištění místa, kde se nachází ohnisko. V jaké vzdálenosti se nachází ohnisko pro daný paprsek? Vyzkoušejte, jestli ostatní odražené paprsky mají stejné ohnisko.

3. Jaký je vztah mezi ohniskovou vzdáleností a poloměrem křivosti? Změňte poloměr křivosti zrcadla v simulaci a celý experiment opakuj. Nyní už byste měli vztah určitě znát.

Závěr

Paprsky, které jsou rovnoběžné s osou zrcadla, odrazí vypuklé zrcadlo jako rozbíhavé. Ohnisko leží za zrcadlem a jeho velikost je polovinou poloměru křivosti.

Pracovní list

Lom světla

Úvod

V této simulaci se budeme zabývat tím, co se stane s paprskem, který dopadá na rozhraní dvou prostředí pod určitým úhlem.

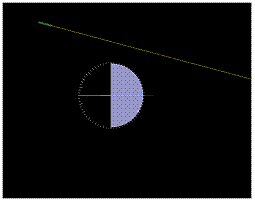
Přechod vzduch-sklo

Otevřete si simulaci.

1. Posuňte zdroj světla tak, aby paprsek směřoval do středu rovné hrany skleněného bloku. (je to místo, kde vystupuje z hranolu červená čára)

2. Postupně měňte úhel dopadu. Paprsek však vždy musí dopadat do středu rovné hrany. Hodnoty úhlů dopadu a odrazu si zapište do tabulky.

α - úhel dopadu	β - úhel lomu

3. Který z úhlů je větší? Úhel dopadu nebo lomu?

4. Jaký je úhel lomu, jestliže je úhel dopadu 0 stupňů?

Přechod sklo-vzduch

Otevřete si simulaci.

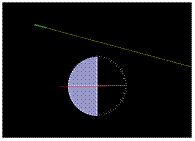
1. Posuňte zdroj světla tak, aby nejprve paprsek procházel zakřivenou částí hranolu a směřoval do místa, kde vystupuje z rovné části červená čára.

2. Postupně měňte úhel dopadu. Paprsek však vždy musí dopadat do středu rovné hrany (nezapomeňte, že musí nejprve procházet zakřivenou částí). Hodnoty úhlů dopadu a odrazu si zapište do tabulky.

α - úhel dopadu	β - úhel lomu

3. Který z úhlů je nyní větší? Úhel dopadu, nebo lomu?

4. Pokuste se najít úhel dopadu (mezní úhel), pro který je hodnota úhlu odrazu blízká 90 stupňům.

5. Co nastane, jestliže překročíte hodnotu zjištěného mezního úhlu?

Závěr

Na rovinném rozhraní dvou optických prostředí nastává lom světla.Postupuje-li paprsek do prostředí, ve kterém se světlo šíří menší rychlostí, např. ze vzduchu do skla, nastane lom paprsku ke kolmici. Postupuje-li paprsek do prostředí, ve kterém se světlo šíří větší rychlostí, např. ze skla do vzduchu, nastane lom paprsku od kolmice.

Pracovní list

Spojky

Úvod

V této simulaci si ukážeme, jak prochází paprsek spojnou čočkou, kde vzniká obraz objektu, jak je velký atd.

Pravidla pro chod paprsků

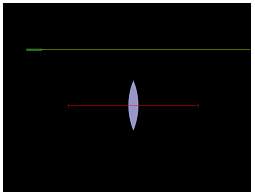Otevřete si simulaci.

1. Červená čára procházející středem čočky se nazývá osa čočky. Posuňte zdroj světla tak, aby paprsek ze zdroje byl rovnoběžný s osou čočky a procházel čočkou. Co se stalo paprsku? Vyzkoušejte několik pozic zdroje.

2. Bod na ose čočky, kterým prochází lomený paprsek, se nazývá ohnisko.

3. Nyní zdroj natočte a opět nasměrujte paprsek na spojku. Co se nyní stalo s paprskem? Co se stane s paprskem, jestliže prochází středem čočky?

4. Nyní nasměrujte paprsek tak, aby procházel ohniskem čočky na levé straně a zároveň směřoval do čočky. Jak se lomí?

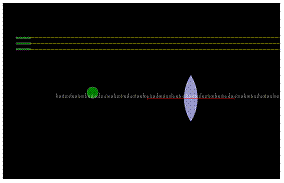Tvorba obrazu

Otevřete si simulaci.

1. K vyřešení problému, kde bude obraz míčku, použijeme tři paprsky a pravidla, která jsme se naučili v první části.

2. Přesuňte první zdroj tak, aby jeho paprsek procházel těsně nad míčkem a byl rovnoběžný s osou čočky.

3. Druhý zdroj přesuňte a natočte tak, aby se jeho paprsek dotýkal míčku z horní části a procházel ohniskem v levé části.

4. Třetí zdroj přesuňte a natočte tak, aby se jeho paprsek dotýkal míčku z horní části a procházel středem čočky.

5. Místo, do kterého se soustřeďují paprsky v obrazové části, je místem vrcholu míčku obrazu. Jaký tedy obraz je?

6. Zopakujte experiment pro různé polohy míčku vzhledem k ohnisku.

Závěr

Při zobrazení předmětu spojkou se vlastnosti obrazu mění se vzdáleností objektu od čočky. Při přibližování objektu z velké dálky je obraz nejprve zmenšený a pak se postupně zvětšuje a vzdaluje od čočky, stále je převrácený a skutečný. Je-li objekt k čočce blíž než ohnisko, pozorujeme přes čočku zdánlivý, zvětšený a přímý obraz.

Pracovní list

Rozptylky

Úvod

V této simulaci si ukážeme, jak prochází paprsek spojnou čočkou, kde vzniká obraz objektu, jak je velký atd.

Pravidla pro chod paprsků

Otevřete si simulaci.

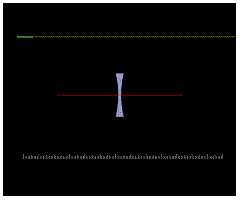
1. Červená čára procházející středem čočky se nazývá osa čočky. Posuňte zdroj světla tak, aby paprsek ze zdroje byl rovnoběžný s osou čočky. Jak čočka lomí paprsek? Přiložte pravítko k paprsku. Kde pravítko protíná osu čočky?

Tento bod se nazývá ohnisko čočky.

2. Nyní posunujte zdroj nahoru a dolů po čočce. Platí stále, že zpětné prodloužení paprsku prochází ohniskem čočky? Co se stane s paprskem, jestliže prochází středem čočky?

3. Natočte a posuňte pravítko tak, aby procházelo ohniskem v pravé části simulace. V dalším kroku posuňte a natočte zdroj světla tak, aby paprsek ležel podél pravítka. Jaký je nyní lomený paprsek?

Tvorba obrazu

Otevřete si simulaci.

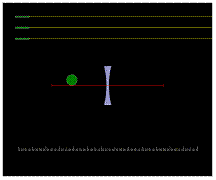
1. Nyní s pomocí znalostí z první části cvičení sestrojíme obraz míčku. Jak bude velký? Bude skutečný? Vzpřímený?

2. Posuňte jeden zdroj tak, aby jeho paprsek procházel osou čočky. (Tento paprsek, protože se dotýká spodní hrany míčku, bude tvořit i spodní část obrazu.)

3. Druhý zdroj posuňte tak, aby byl rovnoběžný s osou a dotýkal se horní hrany míčku.

4. Třetí zdroj posuňte tak, aby se dotýkal vrcholu míčku a procházel středem čočky.

5. Posuňte nyní pravítko tak, aby leželo podél lámané části druhého paprsku. Bod, kde se protíná pravítko a třetí paprsek, ukazuje vrchol obrazu míčku.

6. Jaké jsou tedy odpovědi na původní otázky?

Závěr

Paprsek, který je rovnoběžný s osou čočky, je čočkou lámán tak, že jeho zpětné prodloužení směřuje do předmětového ohniska.

Paprsek, který prochází středem, prochází přímo a není lámán.

Paprsek, který ve zpětném prodloužení směřuje do obrazového ohniska, je lámán čočkou tak, že je rovnoběžný s osou.

Pracovní list

Jednoduchý dalekohled

Úvod

Nyní už víme, jak čočky ovlivňují chod paprsků. V této simulaci si ukážeme využití těchto poznatků v praxi.

Přidání okuláru

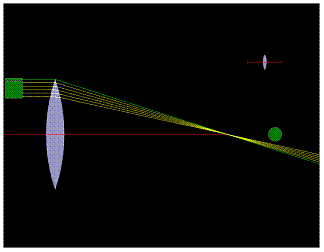Otevřete si simulaci.

1. Rovnoběžné paprsky ze zdroje reprezentují světlo ze vzdáleného objektu. Míček reprezentuje lidské oko. S použitím simulace odpověz na tuto otázku. Proč je obtížné sledovat vzdálené objekty pouze s pomocí jedné čočky?

2. Umístěte druhou čočku mezi první čočku a oko. Kde je nejlepší místo pro umístění této čočky?

3. Druhá čočka se nazývá okulár, který vytváří zvětšený obraz. Jaký obraz vidí oko v naší simulaci? Vzpřímený či převrácený?

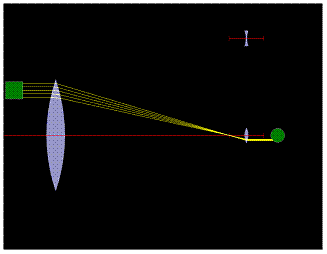
Zdokonalení dalekohledu

Otevřete si simulaci.

1. Pro každodenní používání dalekohledu by bylo pohodlnější, aby obraz předmětu zobrazeného v tomto dalekohledu byl vzpřímený. S použitím simulace se pokus navrhnout takovou úpravu, aby obraz v dalekohledu byl vzpřímený.

2. Kde je nejlepší místo pro umístění rozptylky?

Závěr

Pokud umístíme spojnou čočku s ohniskovou vzdáleností f do vzdálenosti f za ohnisko hlavní čočky, dostaneme dalekohled, jehož obraz je převrácený.

Pokud umístíme rozptylku s ohniskovou vzdáleností f do vzdálenosti f před ohnisko hlavní čočky, dostaneme dalekohled, jehož obraz je vzpřímený.

Pracovní list

Lidské oko

Úvod

Lidské oko je spojná čočka. Zdravé oko dokáže změnit svou optickou mohutnost. U některých lidí se však ostrý obraz vzdálených předmětů zobrazí před sítnicí, přitom blízké předměty takové oko vidí ostře. Takové oko se nazývá krátkozraké. Další případ možné vady oka je, že oko není schopno zaostřit na blízké předměty, jejich obraz je ostrý až za sítnicí. Přitom vzdálené předměty může toto oko vidět ostře. Takové oko označujeme jako dalekozraké. Tyto vady korigujeme brýlemi, tzn. optickou soustavu oka doplníme o další čočku.

Akomodace čočky

Otevřete si simulaci.

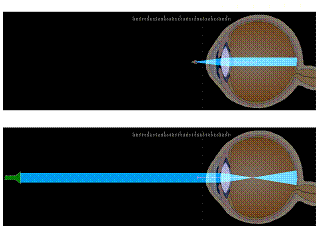
1. Horní simulace nám představuje pohled na blízký předmět a dolní simulace nám představuje pohled na daleký předmět.

2. Změňte ohniskovou vzdálenost čočky v horní simulaci, aby na sítnici dopadal zaostřený paprsek. Všimněte si nového tvaru čočky.

3. Postup zopakujte pro druhou simulaci. Jak se tentokrát změnil tvar čočky?

4. Porovnej ohniskové vzdálenosti jednotlivých čoček.

Korekce zraku

Otevřete si simulaci.

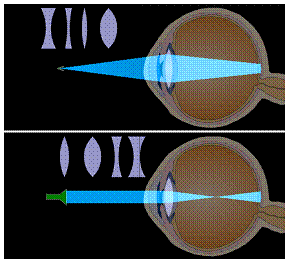
1. Pokuste se opravit vidění každého oka v simulaci s pomocí některé z přiložených čoček. Oko vidí ostře pouze tehdy, pokud dopadá ostrý svazek přesně na sítnici.

2. Z korekcí, které jste provedli, a z pozorování, do kterého místa oči zaostřovaly paprsky, rozhodni, které oko bylo krátkozraké a které bylo dalekozraké.

Závěr

Krátkozrakost oka upravují brýle s rozptylkami. Dalekozrakost oka upravují brýle se spojkami.

Pracovní list

Lom hranolem

Úvod

V této simulaci si ukážeme, jak prochází paprsek hranolem a jak je tento paprsek lámán.

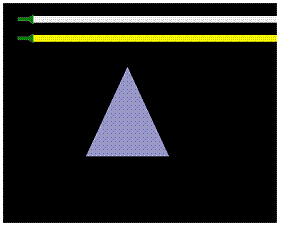
Průchod světla hranolem hranolu

Otevřete si simulaci.

1. Posuňte zdroj žlutého světla tak, aby světlo procházelo hranolem. Co se stalo se světlem po vstoupení do hranolu? Mění se barva paprsku, když opouští hranol?

2. Zopakujte pokus tentokrát se zdrojem bílého světla. Jaké jsou odpovědi na otázky tentokrát?

Jaký je rozdíl v lomu jednotlivých barev?

Otevřete si simulaci.

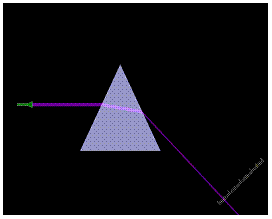
1. Sestavte tabulku pro různé barvy, včetně jejich vlnových délek, jak jsou lámány. Hodnoty odchylky odčítejte z pravítka.

barva a vlnová délka	odchylka

2. Porovnejte hodnoty v tabulce. Která barva je lámána nejméně? Jak je to s vlnovou délkou příslušné barvy?

Závěr

Bílé světlo je složeno z různých barevných světel, proto po dopadu na hranol dochází k rozštěpení paprsku na různé barvy (každá se láme jinak v závislosti na své vlnové délce). Nejméně se láme světlo červené a nejvíce světlo fialové.

Pracovní list

Barvy světla

Úvod

Sluneční světlo je složeno z různých barev. Vy znáte velké množství barev, ale které barvy jsou základní? Jakým způsobem se skládají barvy?

Základní barvy

Otevřete si simulaci.

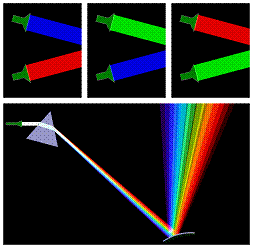
1. V horní části simulace vidíte zdroje světla různých barev. Posuňte zdroje tak, aby se světla překrývala.

2. Jaké jsou barvy ze zdroje? Jaké barvy vznikly překrytím původních barev?

3. Nacházejí se všechny tyto barvy ve spodní simulaci?

Odvozené barvy

Otevřete si simulaci.

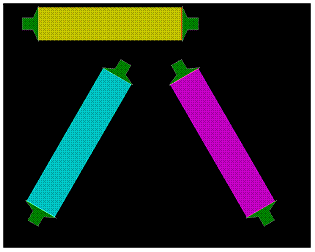
1. Na první pohled byste měli vidět všechny barvy, které vznikly překrytím původních barev v první simulaci.

2. Jaké barvy získáte, jestliže budete míchat tyto barvy?(K tomu, abyste mohli pohybovat oběma zdroji naráz, nejprve klikněte na první, pak držte shift a klikněte na druhý zdroj.)

3. Smíchejte všechny tyto barvy dohromady. Jakou barvu jste získali?

Závěr

Jestliže se překrývají různé světelné paprsky, v místě překrytu vzniká další barva. Základní barvy jsou modrá, červená a zelená. Překrytím těchto barev získáme barvy odvozené. Pokud smícháme všechny odvozené barvy dohromady získáme bílou.