Laboratorní a simulační projekty z elektřiny pro SŠ.

Obsah

Laboratorní a simulační projekty z elektřiny pro SŠ. 1

Přímý link na sestavu. 1

Laboratorní a simulační projekty z elektřiny pro SŠ   ( obsah.cyp)Paralelní a sériové odpory: 1

Paralelní a sériové odpory: 2

Základní měření 2

Děliče napětí: 3

Kirchhoffovy zákony: 5

Princip superpozice: 6

Věty o náhradních obvodech: 7

RLC obvody: 8

Usměrňovače napětí: 9

Stabilizace  napětí - Zenerka. 12

Tranzistory: 13

Pracovní bod toru. 14

Jednoduchý zesilovač s torem.. 14

Operační zesilovače: základní druhy zapojení 16

Generátor pilovitého průběhu. 16

Přímý link na sestavu pokusů

Laboratorní a simulační projekty z elektřiny pro SŠ   ( obsah.cyp)
Paralelní a sériové odpory:

Měření 1 (odpory.cyp):

Měřením zjistěte závislost proudu v sériovém obvodu s jedním rezistorem o odporu 100 Ohm a reostatem o maximálním odporu 500 Ohm pod zdrojem o napětí 5V při různých velikostech odporu na reostatu R_z. Zjistěte, jak závisí napětí na reostatu na jeho odporu, měřením dále zjistěte také závislost velikosti proudu procházejícího obvodem na odporu reostatu. Opakujte měření se zdroji napětí 10 V a 15 V. Výsledky konfrontujte s výpočty.

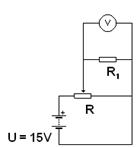
Obvod sestavíme, jak je tomu na obrázku č. 1. Voltmetr zapojíme paralelně k reostatu. Ampérmetr zapojíme sériově se zdrojem.

Výpočet:

Celkový odpor obvodu R je dán součtem odporu na rezistoru R a na reostatu R_z :

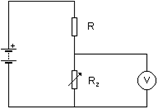
Obr. 1

Proud v obvodu je dán vztahem:

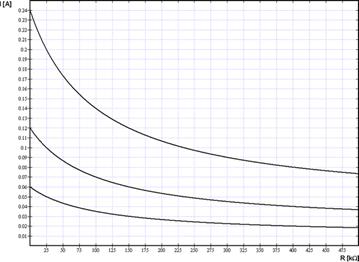
Tento vztah je zaznamenán na obrázku  pro všechny hodnoty uvedené výše.

Napětí na reostatu je:

Toto napětí je zaznamenáno v grafu na obrázku č. 3.

Otázky:

· Jaká úměra platí mezi napětím na rezistoru a odporem reostatu v předchozí úloze?

Zdroj velkého napětí s vysokým vnitřním odporem nebo k němu sériově zapojeným velkým odporem, který je mnohem větší, než je odpor zátěže může posloužit jako jednoduchý zdroj konstantního proudu. Proud v takovém obvodu prakticky nezávisí na odporu zátěže, pokud je alespoň stokrát menší než je odpor u zdroje.

Základní měření

Měření 2: (odpory.cyp)

Sestrojte obvod se zdrojem napětí 5V, který bude měřit proud pro dvě paralelně zapojené soustavy s odpory (rezistor (R₀ = 500 ) a rezistor (R₁ = 100 W) s reostatem

(R_z = 0 – 500 Ohm)), podle obrázku 2, a zaznamenejte, jak závisí celkový proud procházející obvodem na odporu reostatu.  Opakujte pro různé velikosti napětí. Měření konfrontujte s vypočítanými hodnotami. 

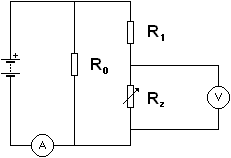
Obr. 2

Výpočet:

Celkový odpor rezistorů s reostatem se rovná:

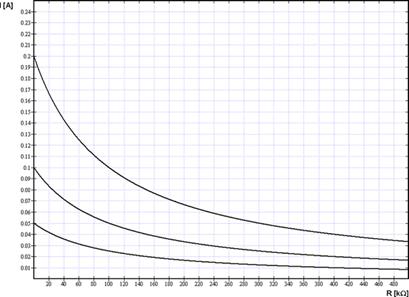
Obr. 3

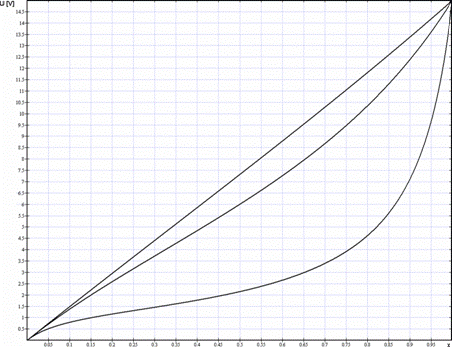
Graficky je tato závislost znázorněna na obrázku 3 pro hodnoty napětí 5V, 10V a 20V.

Otázky:

• Jak závisí napětí na rezistoru R₀ a proud jím procházející na odporu reostatu?
• Bude se napětí na reostatu se zvyšováním jeho odporu zmenšovat nebo zvětšovat?
• Jak by se měnil celkový proud procházející obvodem, kdybychom mohli odpor reostatu zvětšovat k nekonečnu?

Děliče napětí:

Měření 3:(Delice.cyp)

Sestavte obvod podle obrázku č.18 Měřte závislost napětí na rezistoru R₁(100 Ohm) v závislosti na nastavení potenciometru. Naměřené závislosti zaneste do grafu, za předpokladu, že potenciometr je charakterizován dělícím koeficientem x a celkovým odporem R(100 Ohm) a zároveň pro odpor na vstupní části potenciometru platí vztah R_vst = (1 - x)R a pro výstupní R_výs = xR, x náleží do intervalu <0;1>. Zaznamenejte závislosti pro různé hodnoty odporu rezistoru R₁. Výsledky porovnejte s vypočtenou závislostí.

Obr. 4

Výpočet:

Obvod si můžeme představit jako dva sériově zapojené odpory, jeden s velikostí (1-x)R a druhý bude složen ze dvou paralelně zapojených odporů o velikosti xR a R₁. Výstupní napětí, které hledáme je právě napětí na dvou paralelně zapojených odporech.  Součet

tohoto napětí a napětí na prvním odporu se musí rovnat napětí zdroje.

Obr. 5

Proud procházející obvodem bude:

Z těchto dvou rovnic vyjádříme U_výst:

Rovnici můžeme ještě zjednodušit, když podělíme čitatel i jmenovatel R₁ a zavedeme nový parametr a = R/R₁:

Výsledný průběh napětí pro různé hodnoty koeficientu a jsou na obrázku.

Kirchhoffovy zákony:

Měření 4:(kirchhoff.cyp)

Sestavte obvod podle obrázku č.6 a měřte proudy I₁, I₂, I₃ procházející jednotlivými větvemi, pro různé hodnoty odporů R₂, R₃ na reostatech o maximálním odporu 100 kOhm. Velikosti napětí U₁ a U₂ jsou 9 V a 6V. Napište základní rovnice pro napětí ve smyčkách a proudy v uzlech, a vyjádřete pomocí nich závislosti jednotlivých proudů na odporech R1, R2 a R3. Vypočtené výsledky porovnejte s naměřenými hodnotami. 

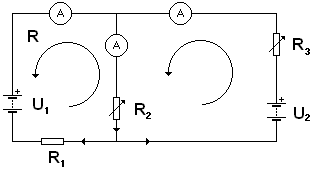
Obr. 6

Výpočet:

      Nejprve musíme zvolit směry proudů v uzlech (nevadí, že skutečné směry neznáme),

například podle obrázku  by platilo

V každé smyčce dále zvolíme kladné směry obíhání. Odpory na nichž je směr proudu souhlasný se směrem otáčení píšeme s kladným znaménkem, odpory, na nichž je směr proudu opačný píšeme se znaménkem záporným. Pro dvě smyčky na obrázku získáme rovnice:

Dále už jen řešíme tři rovnice o třech neznámých. Vztahy pro proudy I₁, I₂ a I₃ vycházejí následovně:

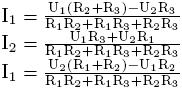
Obr. 7

Otázky:

• Jak velké odpory musíme nastavit na reostatech R₂ a R₃, aby rezistorem R₁ neprocházel žádný proud?
• Co vyplývá pro celkový odpor potenciometru, ze vztahů, které jsme získali z měření 1 a 3?
• Jaké jsou teoreticky dosažitelné hodnoty napětí na odporu R₂ v měření 3?

Princip superpozice:

Měření 5:superpozice.cyp

Sestavte obvod, jako je tomu na obrázku 8, na kterém si ověříme platnost principu superpozice. Hodnoty odporu rezistorů R₁, R₂ a R₃ jsou 20 kOhm, 30 kOhm a 50 kOhm respektive.

Hodnoty napětí U1, U2, U3 jsou 9 V, 15 V a 6V. Postupujte tak, že vždy nechejte zapojený pouze jeden zdroj napětí, a místo ostatních zapojte zkrat. Naměřte pro každý jeden zdroj hodnoty napětí na rezistorech, výsledky sečtěte a porovnejte s naměřenými hodnotami napětí, při kompletním zapojení všech zdrojů.

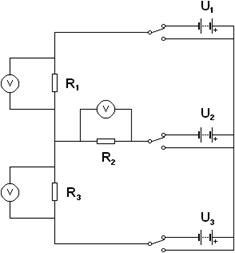
Obr. 8

Věty o náhradních obvodech:

Měření 6:(nahradni.cyp)

Sestrojte obvod se zdrojem napětí U = 10 V a čtyřmi odpory R₁ = 10 kOhm, R₂ = 30 kOhm,

R₃ = 12,5 kOhm a R₄ = 25 kOhm, tak jako je tomu na obrázku 9. Změřte napětí na rezistoru R₄.

Sestrojte náhradní obvod pomocí volitelného zdroje napětí a volitelného odporu, aby napětí na rezistoru R₄ bylo stejné. Výsledek zkonfrontujte s výpočty pomocí Théveninovy věty.

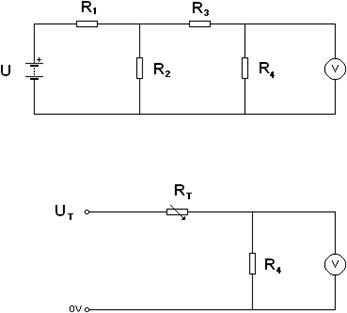
Obr. 9

Výpočet:

Při výpočtu Theveninova napětí je důležité si uvědomit, že obvod v místě rezistoru R₄ považujeme za rozpojený, čili rezistorem R₃ nepoteče žádný proud a Theveninovo napětí bude tedy stejné jako napětí na rezistoru R₂. Jak víme, napětí U se rozdělí na rezistory R₁ a R₂ přímo úměrně jejich odporům. U_T je tedy rovno:

Při výpočtu Theveninova odporu musíme odpory sečíst ve směru od rezistoru R₄ ke zdroji napětí U_T. To znamená, že odpor R₃ je jakoby sériově zapojen se dvěma paralelně zapojenými odpory R₁ a R₂. R_T je tedy:

Měření 7: (nahradni.cyp)

Nahraďte obvod na předchozím obrázku, ale tentokrát místo zdroje elektromotorického napětí použijte ideální zdroj proudu. Výsledek zkonfrontujte s výpočty pomocí Nortonovy věty.

Výpočet:

Náhradní Nortonův odpor bude stejný, jako Theveninův, který jsme spočítaly v předchozí úloze. Zbývá tedy je spočítat velikost ideálního zdroje proudu. Ten se rovná proudu, který procházel větví se zdrojem původního obvodu:

Nortonův náhradní obvod je na obrázku č. 10

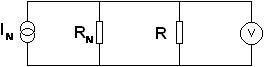
Obr. 10

RLC obvody:

Měření 8: (RLCobvody.cyp)

Sestrojte sériový RLC obvod se zdrojem střídavého napětí, změřte velikost maximálního proudu pro hodnoty napětí U = 2V, kapacity 0,5 mF, indukčnosti 10 mH , pro různé hodnoty frekvence zdroje. Závislost amplitudy proudu na frekvenci zaneste do grafu. Proveďte tato měření i pro různé hodnoty odporu na reostatu R. Najděte maximální napětí na každé součástce obvodu. Porovnejte naměřené hodnoty s výpočty.

Výpočet:

Proud závisí na napětí vztahem I = U/Z, kde Z je celková impedance obvodu. Spočítáme ji podle fázorového diagramu. Jelikož mezi fázovým posunem cívky a kondenzátoru je úhel 180°, vzájemně se odečtou. Rezistor žádný fázový posun nevyvolává, a ve fázovém diagramu je tedy kolmý na reaktanci. Celková impedance je podle Pythagorovy věty:

Závislost proudu na úhlové frekvenci w je na obrázku č.12

Sériové RLC obvody mají využití například u pásmových propustí. To jsou filtry sloužící k potlačení frekvencí jiných, než je rezonanční frekvence obvodu. Signály ležící mimo pásmo propustnosti mají silně sníženou amplitudu a lze je zanedbat. Šířka pásma propustnosti je přímo úměrná odporu R. Za zmínku ještě stojí, že pokud výstupní napětí připojíme na cívku s kondenzátorem místo odporu, získáme tzv. pásmovou zádrž, jejíž funkce je opačná. Pásmová propusť je na obrázku č. 11

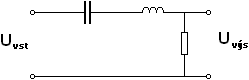
Obr. 11

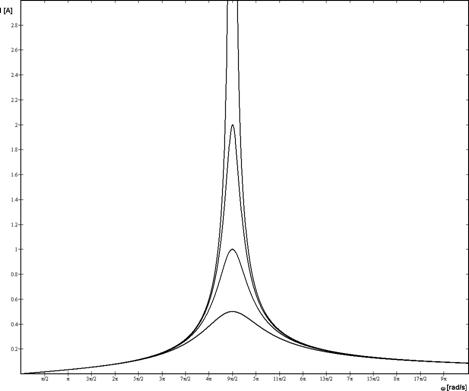
Obr. 12

Usměrňovače napětí:

Měření 9:(usmernovac.cyp)

Usměrňovače se používají k přeměně střídavého napětí na napětí stejnosměrné, takové napětí má ovšem ještě značně proměnlivou amplitudu, a tak se společně s usměrňovači používají i filtry, které usměrněné napětí vyhlazují.

Nejjednodušší způsob usměrnění je jednocestné usměrnění za pomocí jedné diody, jako je tomu na obrázku č.13. Polovodičová dioda je součástka, jejíž propustnost závisí na orientaci napětí. Pokud je napětí orientováno v propustném směru, obvodem prochází téměř stejný proud jako bez diody. V závěrném směru ale dioda téměř žádný proud nepropouští. Sinusoidální napětí zdroje je diodou transformováno na půlvlné napětí.

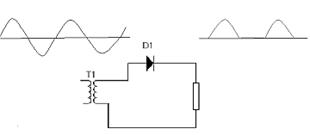
Obr. 13

  U jednocestného usměrňovače se „ztrácí“ polovina napětí, dvoucestné usměrňovače tuto nevýhodu nemají. Jeden možný způsob, jak sestavit takový usměrňovač je na obrázku č. 14. Ten využívá celkem čtyři diody, když je napětí pozitivní prochází proud diodami D1 a D4, když je negativní, prochází proud diodami D2 a D3. Výsledkem je, že negativní část napětí je převrácena podle horizontální osy. Takovémuto zapojení diod se říká Graetzovo.

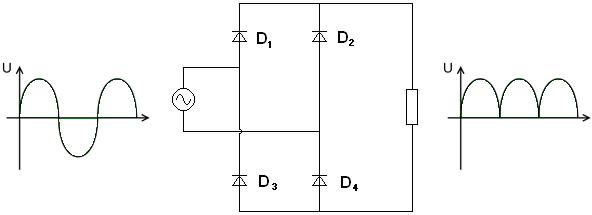
Obr. 14

Dvoucestné usměrnění ale samo o sobě nedodává pro většinu spotřebičů dostatečně vyhlazené napětí. To se řeší pomocí filtrů, které výstupní napětí vyhladí, ideálně až do tvaru konstantního napětí. Všechny takové filtry využívají buď kondenzátory nebo kondenzátory společně s cívkami. Na obrázku  je jednocestný usměrňovač s kondenzátorovým filtrem.

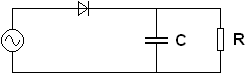
Obr. 15

 Během kladného čtvrt cyklu napětí se kondenzátor C nabije, jakmile napětí klesne pod své maximum, kondenzátor se začne vybíjet přes rezistor R. Výsledné hodnoty napětí na rezistoru R jsou znázorněny na obrázku (červeně) v porovnání s obvodem bez kondenzátoru (modře).

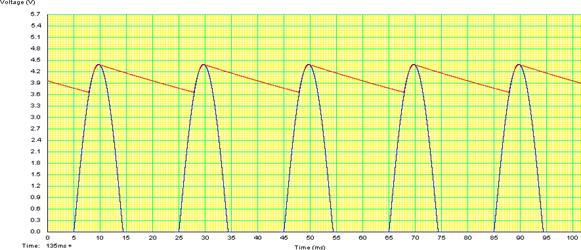
Obr. 16

Nejlepších filtračních výsledků dosáhneme takzvaným p filtrem. Ten využívá dva paralelně zapojené kondenzátory s cívkou, která svou indukčností redukuje zbytkové zvlnění napětí. Při velkých kapacitách kondenzátorů, velké indukčnosti cívky a velkém odporu R lze dosáhnout téměř konstantního průběhu napětí. Na obrázku je zachyceno Graetzovo zapojení s p filtrem.  

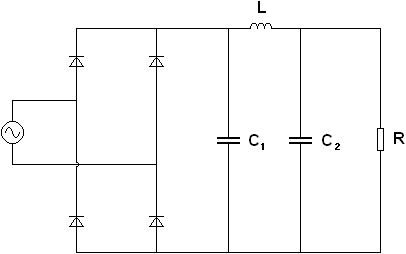
Obr. 17

Kromě filtrů se k další stabilizaci napětí může použít ještě Zenerova dioda.  Jedná se o silně dotovanou diodu s přesně daným průrazovým napětím v závěrném směru. Napětí na takové diodě zůstává téměř stejné bez ohledu na procházející proud. Běžné zenerovy diody mají průrazové napětí od 1,8 V až do 200 V.

Sestrojte různé typy usměrňovačů a sledujte výstupní hodnoty napětí.

Stabilizace  napětí - Zenerka

Měření 10:  (zener.cyp)

Zenerova dioda si udržuje téměř konstantní napětí, ale jen pro určitý interval proudu, jí procházející. Pokud je proud příliš malý či příliš velký, bude mít napětí na diodě již značné odchylky. Sestrojte obvod podle obrázku č. 18, použijte 5,1 V diodu a konstantní zdroj proudu a změřte, jak závisí napětí na diodě na proudu, který jí prochází. K regulaci proudu použijte variabilní rezistor. Výsledek zaneste do grafu.

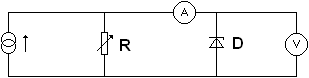
Obr. 18

Zenerova dioda, dokáže udržet téměř konstantní napětí od určitého minimálního proudu, pro velké proudy se napětí na diodě začne mírně zvyšovat, v důsledku malého odporu, který dioda má. Naměřená závislost napětí na proudu je znázorněna zde.

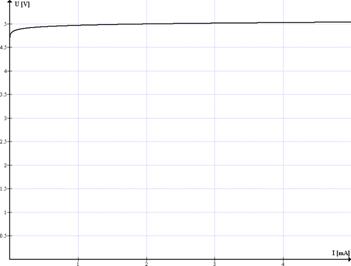
Obr. 19

Tranzistory:

Měření 11: (tranzistor.cyp)

Připojíme-li ke kolektoru zdroj napětí, a začneme jeho napětí postupně od nuly zvyšovat, začne se nejdříve proud procházející kolektorem lineárně zvyšovat s tímto napětím, až do určitého mezního napětí, kdy už zůstane kolektorový proud konstantní. Pokud tuto závislost zaneseme do grafu, kde na horizontální přímku naneseme napětí mezi kolektorem a emitorem U_CE a na vertikální přímku naneseme kolektorový proud I_C, získáme křivku, které se říká charakteristická kolektorová křivka. Sestrojte obvod podle obrázku č.20, měřte kolektorový proud pro různé hodnoty napětí mezi kolektorem a emitorem U_ce. Naměřené hodnoty zaneste do grafu. Opakujte měření pro různé hodnoty bázového proudu. Bázový proud se snažte pomocí reostatu v průběhu měření udržet konstantní.

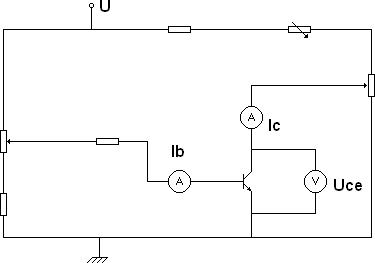
Obr. 20

Charakteristická křivka běžného bipolárního tranzistoru je zde

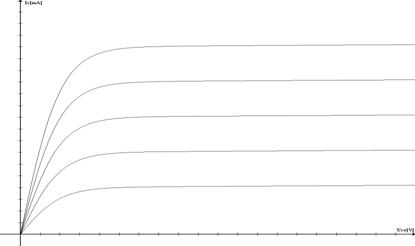
Obr. 21

Pracovní bod toru

Měření 12:(pracovni.cyp)

Využijeme grafu kolektorových křivek, naměřených v předchozí úloze, k nastavení pracovního bodu tranzistoru. Ten bude na místě průniku kolektorové křivky pro daný bázový proud a tzv. zátěžové přímky, ta spojuje bod úplné saturace, který vypočítáme pomocí podmínky, že napětí mezi kolektorem a emitorem je při saturaci teoreticky nulové a tranzistorem prochází maximální proud I_c = U_cc/R_c, a bodu při kterém tranzistorem neprochází žádný proud a napětí mezi kolektorem a emitorem se rovná zdrojovému napětí.

Sestrojte obvod podle obrázku č. 22, nastavte pomocí reostatů nějaký bázový proud, pro který máte naměřenou kolektorovou křivku a najděte na grafu volt-ampérové charakteristiky tranzistoru jeho pracovní bod pro dané zapojení. Zjistěte, zda takto získaná hodnota kolektor-emitorového napětí a kolektorového proudu pracovního bodu odpovídá naměřeným

hodnotám.

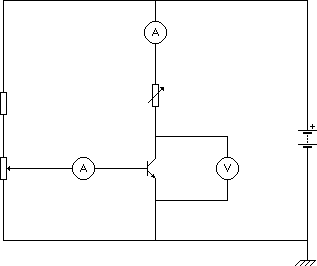
Obr. 22

Jednoduchý zesilovač s torem

Měření 13: (zesilovac.cyp)

Sestavte zesilovací obvod se společným emitorem, použijte malé vstupní napětí, ne více než jeden volt a měřte hodnoty výstupního napětí, pro různé hodnoty odporů R_C, R_E, R₁ a R₂.

Výstupní napětí na takovém zesilovači je rovno kolektorovému napětí na tranzistoru. To se rovná:

U_výs = U_CC - R_CI_C

Princip zesilovače spočívá v tom, že malé změny proudu způsobené vstupním napětím na bázi vyvolají mnohem větší změny proudu na kolektoru, a tím i kolektorového napětí. Jelikož ale báze propouští proud pouze v jednom směru, je vstupní napětí pomocí rezistorů R₁ a R₂ zvýšeno. Napětí na bázi U_báze potom osciluje pouze v kladných hodnotách. Abychom zjistili proud I_C, uvažujme nejprve jaký proud prochází rezistorem R_E, napětí na emitoru se rovná bázovému napětí mínus zhruba 0.7 V a mezi kolektorovým a emitorovým proudem platí vztah I_C = aI_E. Potom vztah pro výstupní napětí můžeme zapsat jako:

U_výs = U_CC - (U_báze - 0,7) aR_C/R_E

Výsledná amplituda napětí je tedy určena především poměrem odporu rezistorů R_C a R_E, alfa je většinou jen málo odlišné od jedničky, a proto ho prakticky nemá cenu brát v úvahu. Výsledné napětí bude také posunuto o 180° oproti vstupnímu napětí. Pro výstupní napětí ale platí určitá omezení, předně nemůže být vyšší než napětí U_CC, a nemůže dosahovat ani příliš nízkých hodnot, protože na tranzistoru dojde k nasycení a kolektorový proud se už dále nebude zvyšovat. Změnou odporů R₁ a R₂ můžeme upravit hladinu, kolem které bude výstupní napětí oscilovat, a tak dosáhnout optimálních výsledků.

Zesílení je charakterizováno konstantou A = U_výs/U_vst, častěji se ale používá zesílení v decibelech A(dB) = 20log(A), při použití více zesilovačů můžeme potom celkové zesílení sčítat. Zapojení se společným emitorem je často následováno zesilovačem se společným kolektorem, takový obvod potom zesiluje napětí i proud. 

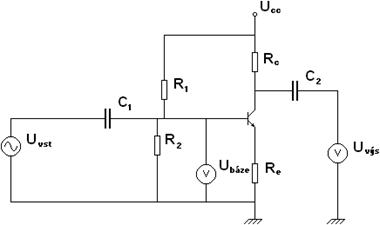
Obr. 23

Příklad možného výstupu pro hodnoty R₁ = 60 kOhm, R₂ = 30 kOhm, C₁ = 50 mF, R_C = 200 Ohm, R_E = 50 Ohm a f = 50 Hz je na obrázku.

Operační zesilovače: základní druhy zapojení

Měření 14:(opamp.cyp)

Sestavte všechny základní druhy zapojení zesilovačů, uvedené v sekci o zesilovačích, a ověřte správnost jejich funkce.

Generátor pilovitého průběhu

Měření 15:(pil.cyp)

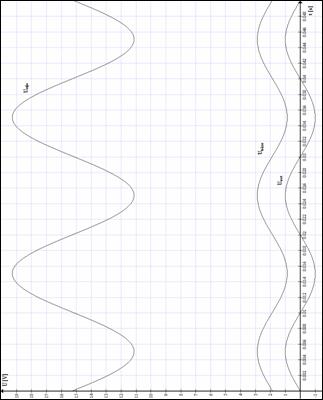
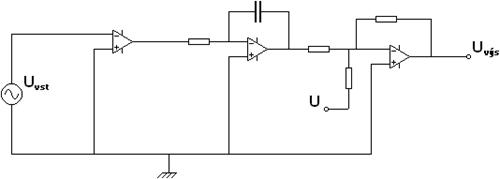
Postavte pomocí operačních zesilovačů obvod, který bude transformovat sinusoidální napětí zdroje na výstupní pilovité napětí, oscilující kolem nuly.

Možné řešení je na obrázku č. 38, vstupní sinusoidální napětí je nejdříve pomocí srovnávacího zesilovače transformováno na čtvercové, to se dále pomocí integračního zesilovače transformuje na pilovité napětí, které ale nemusí nutně oscilovat kolem nuly, a tak je ještě použit sčítací zesilovač k upravení oscilační hladiny.

V programu Crocodile Physics je k dispozici 15 ukázkových obvodů s přednastavenými parametry pro laboratorní cvičení.

Tato práce je určena především pro pedagogy a má sloužit jako učební pomůcka ve výuce elektrotechniky a příbuzných předmětech.